Precedente Indice Successivo



Fsbpk


Scopo: risoluzione di un sistema L*x=b con matrice dei coefficienti L di tipo triangolare inferiore.
Specifiche: subroutine fsbpk(l, b, n, ifail)
integer n, ifail
real l(n*(n+1)/2), b(n)
Descrizione: Backgroud del problema

Il problema riguarda la risoluzione di un sistema lineare con matrice dei coefficienti in forma triangolare inferiore e non singolare. In queste condizioni, la risoluzione è molto semplice se si usa il metodo di sostituzione in avanti (Forward Substitution). Si può spesso ricondursi nelle condizioni richieste, tramite una fattorizzazione della matrice dei coefficienti del sistema in esame

Descrizione dell'algoritmo

L'algoritmo si riduce all'implementazione del metodo forward substitution applicato al sistema L*x=b con L={lij} matrice dei coefficienti e b={b1,...,bn} vettore dei termini noti, che consente di calcolare le incognite del sistema nel modo seguente:

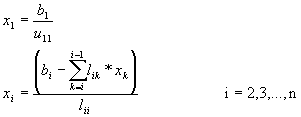
tale metodo è applicabile solo se ogni elemento della diagonale principale della matrice in esame è non nullo, cioè solo se la matrice è non singolare. Per evitare accessi a blocchi di memoria diversi, con conseguente aumento della complessità di tempo, l'algoritmo implementato lavora per colonne.

Raccomandazioni sull'uso

E' essenziale per il funzionamento dell'algoritmo che la matrice sia non singolare. Inoltre, poiché l'algoritmo si trova ad operare su di una matrice sparsa strutturata, che ha un intero triangolo nullo, si preferisce memorizzare tale matrice come un vettore (array formato packed), il che consente una notevole riduzione della complessità sia di tempo, sia di spazio.

Si raccomanda di utilizzare, per la risoluzione di un sistema di ordine n, un vettore di lunghezza n*(n+1)/2, contenente solo gli elementi non nulli della matrice, ordinati per righe. Per ridurre la complessità di spazio, il vettore in uscita della subroutine è lo stesso vettore di ingresso, nel quale erano memorizzati i termini noti del sistema.

Se è necessario un successivo utilizzo di tali valori, si consiglia di salvarli in un opportuno vettore prima dell'uso della subroutine.

Bibliografia: [1], [2]
Parametri di I/O: input

l - vettore di reali, elementi del triangolo inferiore L
b - vettore di reali, termini noti del sistema
n - intero, ordine della matrice

output

b - vettore di reali, soluzione del sistema
ifail - intero, indicatore d'errore
Indicatori d'errore: Errori gestiti dalla subroutine:

ifail = 0 nessun errore
ifail = 3 la dimensione insrita non è valida (non positiva)
ifail = 4 la matrice inserita è singolare

Routines ausiliarie: nessuna
Tempo d'esecuzione: l'algoritmo richiede l'esecuzione di n*(n+1)/2 moltiplicazioni e di n*(n-1)/2 addizioni, la complessità è asintotica dell'ordine O(n2/2)
Memoria richiesta: sono dichiarati due array di dimensione n*(n+1)/2
Accuratezza fornita: metodo esatto a meno del condizionamento della matrice e degli errori di round-off
Esempio di programma chiamante: 
      Program fsbpkd
      
c     Programma dimostrativo della subroutine fsbpk
      
      external fsbpk
      
      integer dim
      parameter (dim=100)
      
      real l(dim*(dim+1)/2),b(dim)             
      integer n,ifail
      character*12 fin,fout
            
      print*
      print*,'*** PROGRAMMA DIMOSTRATIVO DELLA SUBROUTINE FSBPK ***'
      print*
      write(*,10)'Ordine del sistema (max ',dim,') ='
      read(*,*)n      
      print*      
      print*,'Nome del file di input ='
      read(*,'(A)')fin
      open(11,FILE=fin,STATUS='OLD')
      do 1 i=1,n*(n+1)/2
         read(11,*)l(i)
    1 continue
      read(11,*)
      do 2 i=1,n
         read(11,*)b(i)
    2 continue
      close(11)                                 
      print*
      
      call fsbpk(l,b,n,ifail)
       
      if (ifail .eq. 3) stop 'Errore! dimensione non valida'
      if (ifail .eq. 4) stop 'Errore! matrice singolare'
       
      print*,'Nome del file di output ='
      read(*,'(A)')fout
      open(12,FILE=fout)
      write(12,20)(b(i),i=1,n)
      close(12)                    
      
      print*,'Soluzione del sistema ='
      write(*,20)(b(i),i=1,n)
        
   10 format (1X,A,I3,A)
   20 format (1X,E14.7)  
      
      End


Precedente Indice Successivo