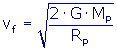Velocità di fuga da un pianeta

applet creata da: Ing. Nando Marturano con: Easy Java Simulations

Istruzioni per l'uso dell'applet:

Velocità di fuga da un pianeta.

  • Disattivare, se attivata, la protezione nei confronti del controllo Java (selezionare consenti contenuto bloccato in alto nel browser).

  • Si consiglia di utilizzare il proprio browser a schermo intero per una migliore visualizzazione dell'applet.

  • Selezionare il pulsante "Start" riportato a fondo pagina, all'interno del riquadro contenente l'applet, per consentirne la partenza.

  • Avviata l'applet, selezionare il pianeta su cui si vuole operare.

  • Immettere il valore della velocità iniziale, che si intende imprimere al corpo posto sulla superficie del pianeta, nella casella evidenziata in giallo.

  • Nella parte destra verranno visualizzate le caratteristiche del pianeta prescelto come la massa media M ed il raggio medio R, la velocità di fuga vf e l'altezza massima che sarà raggiunto dal corpo con la velocità assegnata.

  • Per rientrare sempre nella scala del disegno è necessario assegnare alla velocità valori con un solo decimale; in caso contrario, e solo per valori prossimi alla velocità di fuga, la scala del disegno, a volte, non riesce a visualizzare correttamente le distanze, anche se l'applet funziona correttamente.

  • Premendo il pulsante Play l'applet va in esecuzione e nelle caselle poste in alto verranno segnate le altezze e le velocità raggiunte istante per istante.

  • In qualsiasi momento è possibile mettere in pausa o ripristinare l'esecuzione attraverso i pulsanti Pause e Play.

  • Nell'ipotesi in cui si volesse rieseguire l'applet con valori deversi selezionare il pulsante "Reset" e ricominciare selezionando il pulsante "Avvio".

NB: Si consiglia di utilizzare come risoluzione dello schermo il valore 1024x768 anche se è possibile utilizzare il valore 800x600. Per visualizzare correttamente la simulazione occorre la disponibilità di una connessione veloce e che il vostro browser sia fornito del supporto Java, reperibile gratuitamente al sito http://www.sun.com/it/ 

 

Cenni di teoria:

Velocità di fuga da un pianeta.

 

La velocità di fuga da un pianeta è la velocità minima con la quale un corpo deve essere lanciato dalla superficie di quel pianeta affinché non vi faccia più ritorno.

Supponendo che un corpo di massa m sia lanciato da un pianeta di massa MP e di raggio RP con velocità iniziale v in senso verticale, la sua energia totale, somma dell'energia cinetica e dell'energia potenziale, sarà:

Se la velocità v è sufficientemente piccola, il corpo raggiunge, con velocità nulla, una certa distanza massima hmax dal centro del pianeta e, in quel punto, inverte il suo moto. Per il principio di conservazione dell'energia meccanica si può scrivere:

La condizione che deve verificarsi affinché il corpo di massa m non inverta mai il suo moto è che ad ogni distanza finita dal centro del pianeta la sua velocità si mantenga sempre maggiore di zero. Il caso limite in cui ciò accade si ha quando la velocità tende a zero quando hmax tende ad infinito. In questa condizione il secondo membro dell'equazione precedente vale zero e pertanto si ha:

Da cui è possibile calcolare il valore di v per il quale tale condizione è verificata; tale valore sarà la velocità di fuga Vf.

Si noti come la velocità di fuga da un pianeta sia indipendente dalla massa m del corpo lanciato. Per velocità iniziali maggiori della velocità di fuga dal pianeta il corpo esce dal campo gravitazionale del pianeta mantenendo anche a distanza infinita dal pianeta una energia cinetica finita.