Disattivare, se attivata, la protezione nei
confronti del controllo Java (selezionare consenti contenuto bloccato in
alto nel browser).
Si consiglia di utilizzare il
proprio browser a schermo intero per una migliore visualizzazione dell'applet.
Selezionare il pulsante "Start"
riportato a fondo pagina, all'interno del riquadro contenente l'applet, per
consentirne la partenza.
Innanzi tutto occorre stabilire
se si vuole inserire la funzione da studiare utilizzando la sintassi Java o
una sintassi semplificata. A tale scopo è opportuno leggere, almeno la prima
volta, le istruzioni.
É possibile stabilire, prima di
lanciare la costruzione del grafico, il numero di rotazioni complete che si
desidera siano effettuate.
É possibile valutare il valore della
funzione e delle due coordinate polari assegnando il valore di ø come
qualsiasi frazione di p.
Il cursore sopra
l'area di disegno può essere utilizzato per variare la scala, nel caso in
cui la grafica non rientri nei limiti di visualizzazione.
Ế
anche possibile inserire un proprio valore di Zoom utilizzando la opportuna
selezione che compare sulla sinistra dello schermo.
Il cursore sotto
l'area di disegno può essere utilizzato per modificare la velocità di
riproduzione del grafico della funzione.
Di seguito si riportano alcune
curve polari f(ø), scritte sia con la sintassi
semplificata che con la sintassi Java, sintassi che è consigliabile
utilizzare solo quando occorre assegnare un argomento frazione di
p
all'interno della funzione trigonometrica:
|
Sintassi semplificata |
2*cos(ø) |
1+sin(ø) |
cos(2*ø) |
sin(8*ø/5) |
| Sintassi
Java |
2*Math.cos(ø) |
1+Math.sin(ø) |
Math.cos(2*ø) |
Math.sin(8*ø/5) |
| Sintassi
semplificata |
sin(ø/4) |
ø*sin(ø) |
sin(ø/2) |
1/sqrt(ø) |
| Sintassi
Java |
Math.sin(ø/4) |
ø*Math.sin(ø) |
Math.sin(ø/2) |
1/Math.sqrt(ø) |
| Sintassi semplificata |
cos(3*ø)/sin(3*ø) |
sin(ø/2) |
2*cos(ø) |
e^sin(ø)-2*cos(4*ø) |
| Sintassi
Java |
Math.cos(3*ø)/Math.sin(3*ø) |
2*cos(ø) |
2*cos(ø) |
Math.exp(Math.sin(ø))-2*Math.cos(4*ø) |
| Sintassi semplificata |
sqrt(4*cos(2*ø)) |
sin(5*ø) |
1+4*cos(5*ø) |
sin(ø)+(sin(5*ø/2))^3 |
| Sintassi
Java |
Math.sqrt(4*Math.cos(2*ø)) |
Math.sin(5*ø) |
1+4*Math.cos(5*ø) |
Math.sin(ø)+Math.pow((Math.sin(5*ø/2)),3) |
Ancora si riportano alcune
curve polari f(ø), di cui è indicato il nome e la formula generica, il cui
esempio è scritto con la sintassi semplificata:
|
Spirale di Archimede
r = ± k∙ø
2*ø |
Spirale iperbolica
r =
± k/ø
1/(2*ø) |
Spirale logaritmica
r = e± k∙ø
e^2*ø |
Spirale parabolica
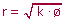
sqrt(4*ø) |
|
Spirale di Fermat

2*sqrt(ø) |
Litus
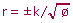
2/sqrt(ø) |
Cocleoide
r = ±k∙sin(ø)/ø
2*sin(ø)/ø |
Lemniscata di
Bernoulli
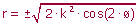
sqrt(2*cos(2*ø)) |
|
Bifolium
r = ±k∙sin(ø)∙cos2(ø)
2*sin(ø)*cos(ø)^2
|
Rodonea o Rosa a tre
foglie
con petalo su asse
verticale
r = ±k∙sin(3*ø)
2*sin(3*ø) |
Rodonea o Rosa a tre
foglie
con petalo ruotato
dell'angolo φ
r = ±k∙sin(3*ø ± φ)
2*sin(3*ø+0.78) |
Rodonea o Rosa a tre
foglie
con petalo su asse
polare
r = ±k∙cos(3*ø)
|
|
Rodonea o Rosa a
quattro foglie
con petali nei
quadranti
r = ±k∙sin(2*ø)
2*sin(2*ø) |
Rodonea o Rosa a
quattro foglie
con petali sugli assi
r = ±k∙cos(2*ø)
2*cos(2*ø) |
Rodonea o Rosa ad n=7
foglie
con petali su asse
verticale
r = ±k∙cos(n*ø)
2*sin(7*ø) |
Rodonea o Rosa ad n=7
foglie
con petali su asse
polare
r = ±k∙cos(n*ø)
2*cos(7*ø) |
|
Concoide di Nicomede
con asintoto
orizzontale
r = ±k/sin(ø) + m
1/sin(ø)+3 |
Concoide di Nicomede
con asintoto verticale
r = ±k/cos(ø) + m
1/cos(ø)+3 |
Cissoide di Diocle
r = 2∙k∙sin(ø)∙tan(ø)
2*sin(ø)*tan(ø)
|
Lumaca di Pascal
±k∙cos(ø) + m
2*cos(ø)+3
|
Per finire vengono riportate
alcune curve polari f(ø) corrispondenti alle classiche curve che vengono
studiate nel piano cartesiano:
|
Retta parallela
all'asse delle x:
r =
±k/sin(ø)
2/sin(ø) |
Retta
parallela all'asse delle y:
r =
±k/cos(ø)
2/cos(ø) |
Circonferenza con centro C=(0,a/2):
r =
±k∙sin(ø)
2*sin(ø) |
Circonferenza con centro C=(a/2,0):
r = k∙cos(ø)
2*cos(ø) |
|
Parabola
(eccentricità e=1):
r =
±k/(1 ± e∙cos(ø))
2/(1-cos(ø)) |
Ellisse (eccentricità
0<e<1):
r =
±k/(1 ± e∙cos(ø))
2/(1-0.5*cos(ø)) |
Iperbole (eccentricità
e>1):
r =
±k/(1
± e∙cos(ø))
2/(1-1.2*cos(ø)) |
|