Transitorio di un circuito RL alimentato a tensione costante

applet creata da: Ing. Nando Marturano con: Easy Java Simulations

Istruzioni per l'uso dell'applet:

Transitorio RL - Transitorio di un circuito RL alimentato a tensione costante.

  • Disattivare, se attivata, la protezione nei confronti del controllo Java (selezionare consenti contenuto bloccato in alto nel browser).

  • Si consiglia di utilizzare il proprio browser a schermo intero per una migliore visualizzazione dell'applet.

  • Selezionare il pulsante "Start" riportato a fondo pagina, all'interno del riquadro contenente l'applet, per consentirne la partenza.

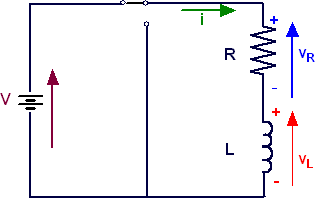
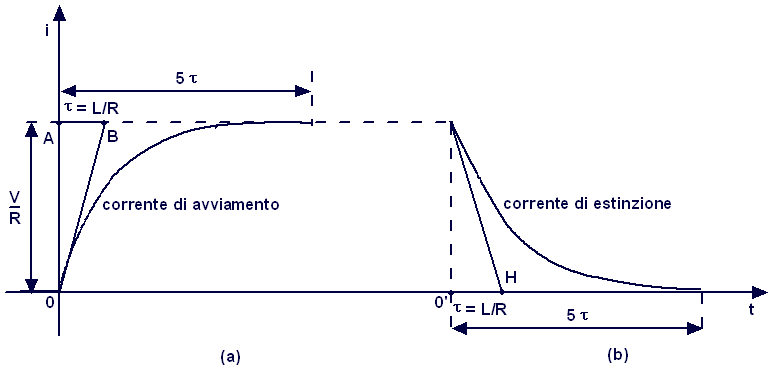
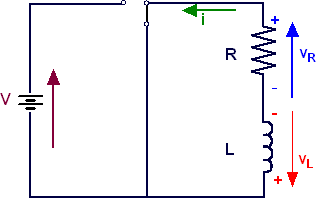
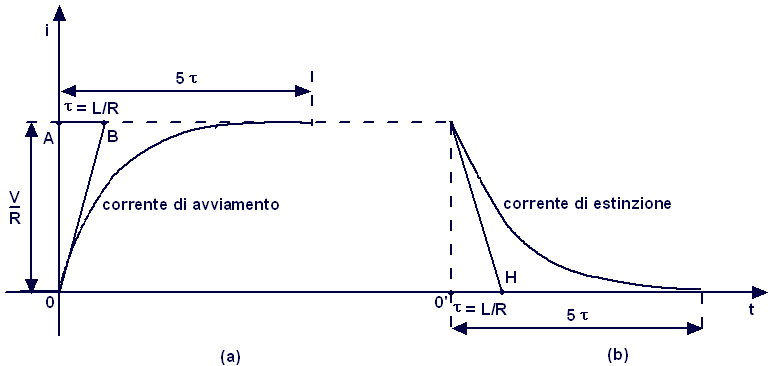
  • Avviata l'applet, risulterà selezionare in modo automatico la casella "transitorio di carica".

  • Immettere i valori di R (espressa in Ω), di L (espressa in H) ed il valore della tensione da applicare V ( espressa in V).

  • Controllare il valore della costante di tempo t ; essa deve assumere un valore almeno dei decimi di secondo affinché si abbia la possibilità di visualizzare con una certa lentezza il fenomeno.

  • Selezionare il valore di k che determinerà il tempo T visualizzato sull'asse delle ascisse secondo la relazione: T = 2·K·t = 2·K·RC . Il valore assunto per default è K = 5, tuttavia è sempre possibile cambiarlo anche durante l'esecuzione dell'applet.

  • Selezionare il grafico della grandezza che si intende visualizzare, ovvero corrente in funzione del tempo i(t), tensioni presenti nel circuito in funzione del tempo V(t), vR(t), vL(t), potenze in gioco nel circuito in funzione del tempo pR(t), pL(t) e pT(t). In alternativa è sufficiente selezionare il pulsante grafici per selezionarli tutti contemporaneamente.

  • In qualsiasi momento è possibile mettere in pausa o ripristinare l'esecuzione attraverso i pulsanti Pause e Play.

  • Quando si desidera passare alla scarica del'induttanza è sufficiente selezionare la casella "transitorio di scarica".

  • Durante l'esecuzione dell'applet è possibile passare più volte dalla carica alla scarica dell'induttanza, costituendo l'unica limitazione il valore assunto per l'asse delle ascisse, che del resto può essere cambiato attraverso la modifica di k, anche durante l'esecuzione dell'applet.

  • I cursori nella parte bassa della finestra possono essere utilizzati per variare con continuità i singoli parametri del sistema per verificarne il comportamento.

  • Nell'ipotesi in cui si volesse rieseguire l'applet selezionare il pulsante "Reset" e ricominciare selezionando il pulsante "Avvio".

NB: Si consiglia di utilizzare come risoluzione dello schermo il valore 1024x768 anche se è possibile utilizzare il valore 800x600. Per visualizzare correttamente la simulazione occorre la disponibilità di una connessione veloce e che il vostro browser sia fornito del supporto Java, reperibile gratuitamente al sito http://www.sun.com/it/ 

Cenni di teoria:

Transitorio RL - Transitorio di un circuito RL alimentato a tensione costante.

 

In un circuito induttivo la corrente per passare da un valore i1 ad un altro diverso i2 impiega un certo intervallo di tempo. Questo tempo è quello che occorre per permettere all'energia magnetica associata alla corrente che è in variazione, di poter variare; infatti un fenomeno energetico finito non può avvenire in un tempo nullo perché occorrerebbe che il sistema, in questo caso il generatore elettrico, fosse dotato di potenza infinita.
Vogliamo qui analizzare il comportamento elettrico del circuito di figura costituito essenzialmente da un generatore di tensione continua di f.e.m. V e di resistenza interna trascurabile (R = 0) e da un bipolo passivo RL serie.

 

Il bipolo RL viene di conseguenza a trovarsi sottoposto bruscamente all'azione della f.e.m. costante (V) del generatore. La corrente però non può portarsi immediatamente al valore finale (V/R) ma ad esso si porta gradatamente impiegando un certo intervallo di tempo, secondo una legge esponenziale come riportato nella figura successiva, nella parte (a).

La sua espressione analitica è la seguente:

dove e è la base dei logaritmi naturali, V rappresenta il valore della f.e.m. del generatore ed R rappresenta la resistenza totale del circuito.
Si noti che il rapporto L/R viene denominato costante di tempo del circuito (simbolo  t ): essa ha le dimensioni fisiche di un tempo (perché l'esponente t·R/L deve risultare adimensionale) e rappresenta quell'intervallo di tempo che sarebbe necessario alla corrente i per raggiungere il valore di regime (V/R) se questa continuasse a salire con incremento costante uguale a quello iniziale. Si dimostra infatti che la tangente nell'origine della curva esponenziale stacca sulla orizzontale di ordinata V un segmento che vale t = L/R.
Concludendo, il fenomeno di avviamento a tensione costante di un circuito RL avviene come segue. Chiuso il circuito, alla tensione V, applicata al circuito in modo brusco, può fare equilibrio solo la f.c.e.m. di autoinduzione dell'avvolgimento la quale assumerà il suo massimo valore, mentre la corrente sarà praticamente nulla.
Durante il periodo transitorio la corrente aumenta e la tensione indotta diminuisce, tendendo a zero col trascorrere del tempo.
A regime la corrente arriva al valore finale e la tensione indotta si riduce a zero (l'induttanza si comporta come un corto circuito).
Il fenomeno sarà terminato quando la corrente i avrà raggiunto il valore V/R. Praticamente ciò avviene quando i differisce da V/R per meno dell'1%. La durata T del periodo transitorio vale allora circa 5·L/R, cioè il fenomeno di carica si può considerare terminato dopo un tempo uguale a circa cinque volte la costante dl tempo del circuito.
 

Transitorio RL - Transitorio di un circuito RL in cui cessa l'alimentazione

 

Quando nel circuito viene soppressa l'azione della f.e.m. (V) del generatore, facendo assumere al commutatore la posizione riportata in figura:

Il bipolo RL si trova ad essere chiuso su se stesso e la corrente i che ha un valore ben definito (V/R) non si annullerà istantaneamente ma la «estinzione» avverrà ancora secondo una legge esponenziale decrescente come riportato in figura b.

La sua espressione analitica è la seguente:

In questo modo si permette all'energia immagazzinata in precedentemente dal campo magnetico nell'induttanza (Wm = ½·L·i2) di diminuire progressivamente fino ad annullarsi (naturalmente per il principio della conservazione dell'energia questa energia magnetica in realtà non si annulla, ma si trasforma in altro tipo di energia, ad es. in calore nella resistenza del circuito).
Per questo motivo la corrente decrescerà con la solita legge esponenziale, tendendo asintoticamente a zero, teoricamente così annullandosi dopo un tempo infinito.
Ma si è ormai capito che la corrente nel circuito si sarà ridotta a meno dell'1% del valore iniziale V/R dopo un tempo uguale a cinque volte la costante di tempo t del circuito (5·L/R), per cui si potrà ancora affermare che il transitorio si considera esaurito dopo un tempo non inferiore a cinque volte la costante dl tempo del circuito.