Matematica: nascita e sviluppo di un Modello-Metagfora del Mondo - prima parte
di Ezio Saia

---

La metafora
Il problema della metafora interessa tanto il campo scientifico conoscitivo quanto quello letterario e va comunque ben al di là del mero sfavillante esercizio letterario. Dove coinvolge l’evasione dal mondo, la creazione di mondi e il ritorno al mondo, il processo di creazione della metafora letteraria pare avere una funzione opposta a quella della metafora conoscitiva. La seconda, consumandosi, perde l’alone metaforico e consolida la conoscenza, la prima, consumandosi, pare chiudere l’accesso ai mondi che aveva aperto.

Parliamo di onde della sabbia, di onde del deserto e s’innesca il meccanismo dell’analogia, una delle figure madri della metafora che ci spalanca un nuovo e misterioso mondo di fantasia e di meraviglie, vengono evocati nuovi mondi con nuovi e favolosi animali come i pesci della sabbia, le balene della sabbia, i polipi della sabbia. Queste esistenze ci fanno sognare e ci trasportano in mondi sconosciuti orrendi o meravigliosi.
Quando l’analogia sfuma nella metafora il meccanismo di generazione è lo stesso. Otteniamo le balene della sabbia applicando le leggi dell’analogia che fanno corrispondere a ogni oggetto ‘configurazione del mare’ un corrispondente oggetto ‘configurazione del mare di sabbia’ così come le onde del mare corrispondono alle onde della sabbia.
Accade come se fosse stata stabilita una legge di corrispondenza applicando la quale vengono fatti corrispondere ad individui (noti) appartenenti ad un mondo “dominato”, individui (ignoti e irreali come i sopra citati pesci della sabbia) appartenenti ad un mondo fantastico.
Ho brevemente parlato di metafore per presentare non una tesi ma un sospetto. Il sospetto che molte entità strane partorite dall’aritmetica e in generale dalla matematica e talvolta sentite come eresie non siano balene della sabbia ma partecipino della vita delle balene della sabbia.

Eresie
Ho parlato di eresie. Ma perché eresie?
Il termina ricorda Borges e molti protagonisti dei suoi racconti le eresie di cui voglio parlare riguardano numeri. Numeri eretici Lo sono in un certo senso i numeri interminabili, i numeri irrazionali, i numeri immaginari, gli indivisibili, gli infinitesimi, gli infiniti, i mondi non standard. Perché eretici e perché ‘balene della sabbia’? Certamente le denominazioni sono suggestive. Evocano l’irrazionalità, i mondi fantastici, gli abissi dell’infinito, i mondi anomali. Ma perché eretici.

Contemporaneo di Galilei, Bonaventura Cavalieri inventò un metodo di calcolo, in cui una linea era una somma infinita di punti, un’area una somma infinita di segmenti e un volume una somma infinita di piani. La sua opera, nota come geometria degli indivisibili, fu giudicata come un tentativo di raccogliere l’acqua con un setaccio. Dice Borges, vero nume tutelare di tutte le eresie.

La vasta biblioteca è inutile. A rigore, basterebbe un sol volume, di formato comune, stampato in corpo nove o in corpo dieci, e composto d’un numero infinito di fogli infinitamente sottili. ( Cavalieri, al principio del secolo XVII, affermò che ogni corpo solido è la sovrapposizione d’un numero infinito di piani).

Cavalieri incredibilmente ottenne grandi risultati. Oltre che confermare risultati già noti, calcolò lunghezze, aree e volumi mai prima calcolati. Nonostante questi successi non riuscì a convincere i contemporanei: quegli strani indivisibili puzzavano troppo di zolfo. Inutilmente si difese sostenendo i suoi indivisibili erano solo scorciatoie.
Gli indivisibili, queste fantomatiche entità che erano e non erano, ma dei quali si doveva comunque parlare, furono presto abbandonati. Con la nuova geometria algebrizzata di Fermat e di Cartesio, gli indivisibili scomparvero, ma nacquero gli infinitesimi loro stretti parenti. La geometria era cambiata, ma anche nella nuova si tornò a parlare di quantità infinitamente piccole e di aree calcolate come somme di infiniti segmenti. Il sospetto che aveva afflitto gli indivisibili si trasferì sui non meno eretici infinitesimi; un sospetto che durò almeno due secoli fino a che Causchy e Weierstrass non inventarono una procedura che otteneva gli stessi risultati, ma non parlava di infinitesimi. L’analisi poté essere trascritta e redenta dal rigore che il nuovo metodo permetteva.
Nonostante ciò, molti manuali d’ingegneria continuarono spesso a lavorare con i troppo comodi infinitesimi fino a che, nella seconda metà di questo secolo, quegli stessi infinitesimi, che secondo Leibniz costituivano la grana fine dell’universo accessibile solo all’intelligenza infinita di Dio, si presero la rivincita, divenendo legittimi e non eretici cittadini nei mondi dell’analisi non standard inventata ( o scoperta o costruita, o fondata) da Robinson.
La controversie degli infinitesimi non fu solo logica matematica ma coinvolse anche l’emergente concetto di razionalità vantato dagli illuministi nei confronti nella ‘non razionale dottrina della fede’

Furono gli illuministi a contrapporre al dogma delle religioni rivelate e alle loro crudeltà monopoliste del sapere, i diritti della ragione. Una ragione che col dubbio, la critica, il pensiero rivendicava il diritto di sottoporre le teorie, i dogmi, le credenze al suo tribunale. Questa rivendicazione ricompare nella successiva Rivoluzione Francese come Dea Ragione ed è ancor oggi un fondamento del pensiero laico che pur non appellandosi alla dea Ragione, rivendica comunque i diritti dell’uomo a stabilire canoni, sensi e metodi per decidere ciò che si può accettare e in che misura.
Ma è possibile definire il senso di termini quali ‘razionalità’, ‘ragione’, ‘razionale’? Cercheremo ora la varietà dei relativi campi di senso, non in generale, ma in relazione alla ragione illuminista e al rapporto con la ‘ragione’ scientifica.
A questo scopo esamineremo brevemente ad alcune situazioni paradigmatiche e altamente significative quali la riforma del sistema di misura e la controversia sugli infinitesimi, in quanto casi esemplari accanto all’ambiguità di certe sopravvivenze magiche nella stessa scienza, lungo un percorso ‘critico’ della ragione illuminista in contrapposizione a un altro percorso più ‘duro’ e dogmatico che da Leibniz e Rousseau, porta a Hegel e Comte.

Gli infinitesimi e Berkeley
Contemporaneo di Galilei, Bonaventura Cavalieri inventò un metodo di calcolo, in cui una linea era una somma infinita di punti, un’area una somma infinita di segmenti e un volume una somma infinita di piani. La sua opera, nota come geometria degli indivisibili, fu giudicata come un tentativo di raccogliere l’acqua con un setaccio.
Cavalieri incredibilmente ottenne grandi risultati. Oltre che confermare risultati già noti, calcolò lunghezze, aree e volumi mai prima calcolati. Nonostante questi successi non riuscì a convincere i contemporanei: quegli strani indivisibili puzzavano troppo di zolfo. Inutilmente si difese sostenendo i suoi indivisibili erano solo scorciatoie.
Gli indivisibili, queste fantomatiche entità che erano e non erano, ma dei quali si doveva comunque parlare, furono presto abbandonati. Con la nuova geometria algebrizzata di Fermat e di Cartesio, gli indivisibili scomparvero, ma nacquero gli infinitesimi loro stretti parenti. La geometria era cambiata, ma anche nella nuova si tornò a parlare di quantità infinitamente piccole e di aree calcolate come somme di infiniti segmenti.1 Il sospetto che aveva afflitto gli indivisibili si trasferì sui non meno eretici infinitesimi;
L’Analisi ottenne un grandioso sviluppo, nonostante l’incomprensibile e oscura irrazionalità di quegli “infinitesimi” che costituivano la sua base concettuale. La situazione era così ‘razionalmente’ disastrosa, che fu facile, anche per un non addetto ai lavori come il vescovo Berkeley, provocato dall’astronomo Halley “sull’inconcepibilità delle dottrine cristiane” ritorcere quelle stesse accuse contro il celebrato Calcolo e rispondere:

“Chiederò per me il privilegio del Libro Pensatore e mi prenderò la libertà di ricercare sull’oggetto, sui principi, e sul metodo di dimostrazione ammessi dai matematici del tempo presente, con la stessa disinvoltura con cui voi presumete di trattare i principi e i misteri della religione.”

E, dopo questo esordio, passare subito al punto dolente del concetto di infinitesimo. Che senso ha affermare che 9,8 + 4,9dt è la stessa cosa che 9,8?

“4,9dt è qualcosa o è nulla; se è nulla tutto il calcolo salta, se è qualcosa le due espressioni non sono uguali. Forse i matematici intendono che 4,9dt è così piccolo da essere trascurabile?” Si chiede Berkeley “Ma, se è questo che intendono, dove va a finire quel rigore inflessibile che li inorgoglisce e che li induce a sostenere che in rebus mathematicis errores quam minimi non sunt contemnendi?”.

Insomma conclude Berkeley nessuna dottrina teologica è così razionalmente oscura e inconsistente come queste teorie matematiche. Se la teologia richiede la fede perchè è inconcepibile, allora che dire delle teorie dei matematici?
Leibniz vide nella ragione lo strumento infallibile per arrivare a dirimere ogni questione e a risolvere ogni problema. Non solo nutrì questa fiducia ma individuò nella logica formale fondata da Aristotele e dagli stoici lo strumento da riformulare e perfezionare fino al raggiungimento di quello scopo. La sua fiducia nella logica come strumento di calcolo era tale da fargli affermare che gli uomini in futuro di fronte a una disputa avrebbero potuto sedersi in pace e calcolando risolvere la disputa discriminando il vero dal falso.
Con Hume, come è noto, la ragione illuministica si fa scettica e la lettura di Hume causò in Kant un totale cambio di prospettiva che lo stesso Kant caratterizzò come un “Risveglio da un sonno dogmatico.” Si potrebbe pensare in base a queste parole, a un precedente Kant sottomesso ai dogmi della religione, ma già prima di leggere Hume, Kant, attraverso gli epigoni dell’illuminista Leibniz (come Wolff), abbracciava una visione illuministica del mondo. Ma allora perché Kant caratterizza questo periodo del suo pensiero come sonno dogmatico, se non considera dogmatico quel tipo di illuminismo? L’episodio mostra chiaramente come l’illuminismo viaggiasse per strade molto differenziate. Kant lo testimoniò chiaramente interpretando la sua conversione da un illuminismo da lui definito ‘sonno dogmatico’ a un altro che riservava alla ragione non compiti di costruzione razionale ma piuttosto compiti di demolizione di concetti consolidati, che, come il concetto di causa, erano considerati veri e propri di dogmi filosofici.
La successiva speculazione di Kant è dunque ancora illuminista. Lo è per la centralità dell’uomo come fonte di acquisizione della verità, per le capacità dell’uomo di ordinare i dati sensibili, e per la funzione critica assegnata all’attività filosofica volta a determinare i limiti della conoscibilità umana, al fine di evitare ogni forma di dogmatismo sia quello di stampo tradizionale e teologico sia quello razionalista di impronta illuminista. Con la Critica della Ragion Pura vengono abbattute la possibilità di pervenire con la ragione al mondo, all’anima a Dio e si demolisce l’idea che con la ragione si possa pervenire a risolvere ogni problema.

La questione di Newton
Il meccanicismo di Cartesio pareva aver eliminato tutte le ‘azioni a distanza’ tipiche delle filosofie naturali precedenti. Con la sua legge sulla conservazione della quantità di moto, Cartesio poté offrire una spiegazione ‘razionale’ tanto degli eventi fisici osservabili sulla terra che del funzionamento e della formazione dell’universo. Una stessa legge era sufficientemente esplicativa e valeva nel microcosmo come nel macrocosmo; una stessa legge valida per tutto l’universo diveniva quel principio di ‘razionalità’ che permetteva agli scienziati di dichiarare sconfitto l’animismo della magia, dell’alchimia, dell’occulto delle forze invisibili benigne o maligne a cui si ispiravano ‘l’irrazionalità’ delle precedenti filosofie della natura la cui caratteristica era proprio la mistica ‘azione a distanza’.
Quando Newton pubblicò i suoi risultati, il mondo scientifico dovette constatare che tutta la capacità esplicativa del suo sistema si basava sulla legge della gravitazione universale che presupponeva l’esistenza di una forza (quella di gravitazione) che agiva a distanza.
La fisica di Newton era assai più esplicativa di quella di Cartesio; tutti i fenomeni meccani dal moto dei pianeti, alla caduta dei gravi potevano essere ‘calcolati’ ma, ripristinando l’azione a distanza, la legge di gravitazione universale, pareva riportare la spiegazione fisica all’irrazionalità della magia e delle ‘influenze’ che a molti parve un regresso verso l’occulto.
Per questa ragione per molti anni la fisica di Cartesio riuscì a conservare fautori accaniti. Più in avversione al ‘magico’ della gravitazione di Newton che in adesione alla sua fisica dell’urto.
Il tentativo di rendere accettabile la fisica di Newton passò dunque attraverso una ‘razionalizzazione’ intesa come via di unificazione sotto un’unica legge, prima tentando di ridurre la seconda (di Newton ) alla prima (quello di Cartesio) e solo in un secondo di ridurre la prima alla seconda.
Il tentativo di ridurre la fisica dell’urto, del meccanicismo dell’orologio a quella dell’azione a distanza era significativo perché in un certo senso ci dice che l’accettazione di una certa idea, anche quella mostruosa dell’azione a distanza sia in gran parte determinata dal tempo e dall’abitudine. Se un’idea ci sconvolge, la difficoltà di confutarla e il tempo ci aiutano a metabolizzarla e ad accettarla.
E’ significativo il tentativo di Boscovich (1711- 1787) che testimonia quanto ormai la nuova forza newtoniana dell’azione a distanza, prima giudicata irrazionale magica e incomprensibile, era divenuta ormai l’unico vero paradigma di comprensione mentre, al contrario, il ‘comprensibile’ e laico urto suscitasse dubbi di razionalità. Nello svolgersi dell’urto fra due bilie, come sottolinea Boscovich, si può passare per entrambe di colpo e con discontinuità dall’immobilità al movimento. Più in generale la bilia A che colpisce passa di colpo da una velocità V1 a una V2, e la B, che è colpita, passa di colpo da una velocità V3 a una V4 e questo costituisce un’evidente violazione di quel principio di ‘comprensibilità’ secondo il quale la natura in generale e la velocità della biglia in particolare non fa salti.
Ciò induce Boscovich a suggerire che ogni corpo agisca sugli altri secondo una doppia forza di attrazione e repulsione, entrambe a distanza. La prima diminuisce con la distanza mentre la seconda, sempre con la distanza, aumenta ma in maniera molto più forte. Quando una bilia si dirige contro una un’altra la sua forza di repulsione aumenta progressivamente vincendo prima la forza di attrazione e poi diventando così forte man mano che si avvicina da spostare l’altra bilia. Quando la distanza fra le due è piccola viene percepita come un urto, mentre in realtà il contatto non avviene.
Il decrescere e l’incrementarsi della velocità in modo continuo veniva poi spiegato in coerenza con le idee dello spazio e del tempo, ma questo esula in parte dalla nostra discussione.

Il modello matematico: modello e metafora del mondo?
La geometria e l’aritmetica nacquero da problemi pratici, di conteggio, di contabilità, di misura di altezze, di angoli, di distanze.
La loro verità nasce dalla prova e la prova è inizialmente pratica, tanto in aritmetica che in geometria: conteggi, merci, pesi, debiti, crediti, lunghezze, superfici. E’ probabile che embrioni d’aritmetica e di geometria nascessero convalidati dalla verifica empirica ma tutto cambiò con Pitagora e la sua scuola quando il numero assunse una funzione metafisica, scientifica e religiosa: non solo di essenza delle cose ma di principio generatore ed esplicatore della realtà capace di svelare la struttura nascosta del mondo.

Il sistema dei numeri assunse lo statuto di fondamento e di modello del mondo. Il modello, inizialmente aritmetico, fu certamente accompagnato da una crescita delle conoscenze geometriche. Certamente uguaglianza, scomponibilità e combinabilità delle figure, similitudine tra i triangoli, operazioni usuali nel calcolo di terreni, di altezze ecc. passarono gradualmente al rango di problemi sulla carta con figure idealizzate. Questa idealizzazione fu un passaggio fondamentale per l’emancipazione della future scienze aritmetiche e geometriche. La possibilità in base ai criteri di similitudine di ricavare relazioni e quindi valori di misura che non dovevano essere convalidati dall’esperienza, fornì, ad esempio, un embrione di dimostrazione e del concetto di dimostrazione, consentendo una prassi, nata nelle conferme, in virtù della quale nacque la parola “dimostrato” da affiancare e/o identificare con “vero”. Fu l’inizio di una confusione che dura ancor oggi.

Con Pitagora la funzione del sistema dei numeri come modello del mondo sta già nel concetto: capisci le relazioni fra i numeri e capirai la relazione fra le cose del mondo, capisci i numeri e capirai i cieli e le stelle.
Il credo pitagorico sarà ripreso da Platone che dedicherà, con la sua scuola, massima cura allo studio della geometria e al mondo dei numeri, un mondo che costituirà, nel suo sistema filosofico, il livello immediatamente precedente al mondo delle idee. Senza la conoscenza delle figure, dei numeri e delle loro proprietà l’accesso alla vera conoscenza è impossibile e l’uomo rimane incatenato alla caverna, al mondo delle ombre, ai sensi, alle apparenze senza mai approdare a quel regno di perfezione, verità e bellezza che è il mondo delle idee.
Le teorie dei pitagorici furono fondanti per la civiltà occidentale e se, per un verso, Omero ne fu un padre, un altro padre, non meno importante, fu Pitagora.
Il modello di Pitagora, benché molto astratto, implica il concetto di misura numerica e quindi la completa descrizione e conoscenza del mondo.
Il numero, misura di tutte le cose, serve per contarle, paragonarle, sommarle, misurarle. Interrogando i numeri interrogheremo il mondo perché il mondo è fatto di numeri, perché il numero è l’essenza metafisica del mondo.
Coi numeri si misurano aree, lunghezze, volumi. Coi numeri si misurano quantità e valore delle merci, tempi e percorsi, debiti e crediti; coi numeri si progettano case e fortificazioni. Nulla pare sfuggire al loro potere conoscitivo.
Pitagora e i suoi allievi furono probabilmente influenzati da questa grande potenza. Se tutto, animali, vegetali, pietre, manufatti, volumi, superfici, poteva essere misurato dai numeri, se uno stesso numero caratterizzava il numero delle cipolle in una cassa, la lunghezza di un cammino, i passi fra due case, la superficie di un campo e tutte le possibili cose, allora il numero, capace di rappresentare un’infinità di cose depurate di tutti quei predicati che li rendevano quelle cose, non poteva che essere l’anima delle cose.
Numeri che potevano, essere addizionati, moltiplicati, sottratti al mercato di Atene o a quello di una qualsiasi altra città, applicati alle stelle in cielo come ai campi di Argo, scritti sulle tavolette di cera, ma anche nella mente di ognuno, quasi che quel campo, quella cassa del mercato, quel gruppo di stelle fossero spiritualmente presenti sul tavolo di casa e accompagnassero l’evolversi degli eventi dal loro nascere al loro morire come durature e stabili essenze generatrici.
Il sistema dei numeri divenne così il sistema modello per il mondo. Le leggi dei numeri, le leggi del mondo. Un’essenza capace di essere evocata a rappresentarle in ogni situazione. Ma il modello non tardò a ribellarsi

La ribellione del numero
I primi dubbi sulla “verità” del modello dovettero nascere già con la divisione fra due numeri che a volte generavano numeri interminabili. 10/3 dà come risultato un infinitivo serie di numeri tre senza alcuna speranza che la serie abbia un termine. Cosa rappresentava questo mostro? Come appariva ai Pitagorici un numero interminabile che nessuna vita, che nessuna infinità di vite poteva sperare di portare a compiutezza? Un mostro che evidentemente nella realtà non pareva essere l’essenza di alcunché. Ma i Pitagorici per cui il numero era misura e relazione, quel numero interminabile potevano comunque essere visto come relazione esprimibile come rapporto di due interi che avevano l’unità come comune unità di misura anche se, comunque, quegli strani interminabili numeri che germinavano da normali operazioni dovettero suscitare qualche perplessità. Che senso può avere il fatto che la lunghezza di un segmento sia misurata da un numero senza fine? Questi numeri interminabili sono già pesci della sabbia?
Il peggio – un peggio irrimediabile – arrivò quando i pitagorici si imbatterono in quella vera assurdità, dimostrabile come vera, secondo la quale non esisteva alcuna unità di misura comune fra il lato e la diagonale del quadrato. Che fare di questi nuovi mostri? La situazione era tragica e i pitagorici la sentirono come tale perché il modello cadeva.
Cadeva davvero? L’Aritmetica intesa come modello del mondo era solo un’immensa metafora che aveva generato non solo pesci ma addirittura mostri di un altro mondo? Certamente rappresentò sia il crollo di una fede sull’onnipotenza dei numeri che il crollo del mondo dei numeri come modello del mondo, un modello che si spostò alle figure dei geometri.

Numeri immaginari
Cavalchiamo i secoli e facciamo un salto in pieno Rinascimento quando gli algebristi si imbatterono in operazioni del tipo

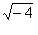
che, ovviamente, non avevano alcun senso né potevano generare un risultato perchè non esistono numeri che hanno per quadrato numeri negativi. Poiché alcuni di questi mostri si presentavano in calcoli di cui già si conoscevano soluzioni, i nostri baldi algebristi non si scoraggiarono e, indicato col simbolo J2 il valore di
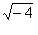dove il simbolo J significava immaginario, proseguirono nei loro calcoli.
Sapevano che JxJ ossia J² era uguale a -1 e impararono presto a sommarli, a moltiplicarli a dividerli fra loro e coi numeri reali, constatando che spesso questi numeri immaginari sparivano e permettevano di portare regolarmente a termine i calcoli.
Avevano trovato altri pesci della sabbia? Uscivano dal nostro mondo per entrare in un mondo immaginario in cui i pesci e le balene della sabbia sguazzano allegramente nei deserti?
L’espressione
Ax + jy somma di un numereo reale con un numero immaginario (ad esempio 3+j2) viene chiamato numero complesso.
La teoria dei numeri complessi ha esiti sconcertanti. Una circonferenza e una retta s’intersecano o non s’intersecano. La circonferenza di raggio 1 e la retta parallela all’asse delle ordinate che passa per P(2, 0) come rappresentato in figura 3,

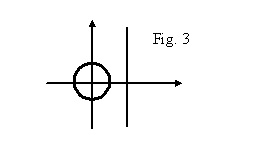
non s’intersecano e non hanno, quindi, punti in comune; ma se consideriamo le loro equazioni 1) e 2)
1) X2 + y2 = 1
2) X= 2

Risolvendo il sistema scopriremo che ha le due soluzioni immaginari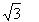e J e - j 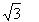e quindi due punti in comune ci sono. Ma si incontrano o non s’incontrano? Il teorema di Gauss ci garantisce che immaginari o no questi punti in comune esistono. Dove, in quale universo, esistono questi punti in cui s’incrociano la circonferenza e la retta in figura?

Secondo Mach la razionalità non riconduce “la non intelligibilità ” a “intelligibilità”, ma piuttosto “si riconducono inintelligibilità insolite a intelligibilità usuali”.(2)
Siamo così abituati alle intelligibilità insolite dei numeri interminabili, degli incommensurabili, degli immaginari, siamo così distratti dalle proficue applicazioni di questi numeri da averli resi intellegibilmente usuali mascherando il loro aspetto di balene della sabbia del nostro modello-metafora di comprensione e percezione del mondo?
Se per un attimo identifichiamo il nostro mondo con quello del modello, come in effetti ci siamo abituarti a fare, allora dire che usciamo dal nostro mondo per entrare in un altro equivale a dire che siamo giunti ad un limite della nostra capacità di comprensibilità utilizzando quel modello come mondo?
Cosa vuol dire che siamo usciti dal nostro mondo e siamo entrati in un altro in cui l’incontro tra quella circonferenza e quella retta avviene? Che quei punti sono inesistenti? Quei punti esistono. Il problema sta nel significato di quell’’esistono’. Come e dove esistono?
Ma a parte le considerazioni d’esistenza molte possibili metafore ci colpiscono. Anche noi talvolta abbiamo bisogno di uscire dal mondo e entrare nell’immaginario. E’ un mondo così difficile, duro insopportabile da indurci a evadere a rifugiarci più o meno permanentemente in altri mondi che non stessi forgiamo nell’universo dell’immaginario. La poesia, il romanzo ecc. sono armi formidabile tanto per questa attività vivificatrice di ripristino quanto per insegnarci a vedere ciò che non siamo mai riusciti a vedere nel nostro. La cultura allarga, dilata i nostri orizzonti. Non è solo telescopio ma anche microscopio.
Quando noi leggiamo autori Kafka, Tolstoj ecc. colloquiamo con loro in uno spazio immaginario, da loro stessi aperto quando scrivevano per i futuri lettori, quando s’affaticavano per rendere migliori i loro testi, più comunicabili le loro emozioni, più seducenti le loro scritture.
Ancora gli infinitesimi
Facciamo un altro salto in avanti e approdiamo, agli inizi del calcolo infinitesimale, a quelle vere bestie nere che furono per filosofi e matematici gli infinitesimi.
Una filigrana di eresie percorre la storia canonica della matematica.
Contemporaneo di Galilei, Bonaventura Cavalieri inventò un metodo di calcolo, in cui una linea era una somma infinita di punti, un’area una somma infinita di segmenti e un volume una somma infinita di piani. La sua opera, nota come geometria degli indivisibili, fu giudicata come un tentativo di raccogliere l’acqua con un setaccio. Dice Borges, vero nume tutelare di tutte le eresie:

La vasta biblioteca è inutile. A rigore, basterebbe un sol volume, di formato comune, stampato in corpo nove o in corpo dieci, e composto d’un numero infinito di fogli infinitamente sottili. (Cavalieri, al principio del secolo XVII, affermò che ogni corpo solido è la sovrapposizione d’un numero infinito di piani).

Cavalieri incredibilmente ottenne grandi risultati. Oltre che confermare risultati già noti, calcolò lunghezze, aree e volumi mai prima calcolati. Nonostante questi successi non riuscì a convincere i contemporanei: quegli strani indivisibili puzzavano troppo di zolfo. Inutilmente si difese sostenendo i suoi indivisibili erano solo scorciatoie.
Gli indivisibili, queste fantomatiche entità che erano e non erano, ma dei quali si doveva comunque parlare, furono presto abbandonati. Con la nuova geometria algebrizzata di Fermat e di Cartesio, gli indivisibili scomparvero, ma nacquero gli infinitesimi loro stretti parenti. La geometria era cambiata, ma anche nella nuova si tornò a parlare di quantità infinitamente piccole e di aree calcolate come somme di infiniti segmenti. (1) Il sospetto che aveva afflitto gli indivisibili si trasferì sui non meno eretici infinitesimi; un sospetto che durò almeno due secoli fino a che Cauchy e Weierstrass non inventarono una procedura che otteneva gli stessi risultati, ma non parlava di infinitesimi. L’analisi poté essere trascritta e redenta dal rigore che il nuovo metodo permetteva.
Nonostante ciò, i manuali d’ingegneria continuarono a lavorare con i troppo comodi infinitesimi fino a che, nella seconda metà di questo secolo, quegli stessi infinitesimi, che secondo Leibniz costituivano la grana fine dell’universo accessibile solo all’intelligenza infinita di Dio, si presero la rivincita, divenendo legittimi e non eretici cittadini nei mondi dell’analisi non standard inventata ( o scoperta) da Robinson.
E che dire delle geometrie non euclidee?
Questo tormentone proveniva da un dubbio tanto antico quanto irrisolto circa la validità dell’assioma3 delle parallele formulato da Euclide. L’assioma, che recita che se P è un punto e a una retta, per P passa una sola parallela ad a, apparve subito sospetto. Altrettanto sospetto doveva apparire a Euclide che lo aveva introdotto, non con gli altri assiomi, ma dopo aver dimostrato una trentina di teoremi. Questa strana collocazione fu subito interpretata come se lo stesso Euclide volesse far capire di averlo introdotto solo perchè non poteva più farne a meno.
L’idea che il mondo non fosse euclideo era così eretica che non venne neppure presa in considerazione. La dimostrazione dell’assioma divenne, così, un’ossessione. Nei secoli si accumularono oltre mille ufficiali e inutili tentativi di soluzione e non furono pochi i matematici che dedicarono alla soluzione del problema la loro vita. Wolfang Boylai, padre di quel Giovanni che diede una svolta definitiva all’enigma, fu fra questi.
Una mezza svolta l’aveva già impressa il matematico Gerolamo Saccheri di Pavia. Questi negò l’assioma delle parallele e sviluppò un nuovo sistema. Saccheri sperava di imbattersi in un “assurdo” che dimostrasse che Euclide aveva ragione e lo volle così tanto che finì per trovarlo anche dove non c’era.
Ciò che Saccheri aveva iniziato era una geometria non euclidea. Dopo di lui, altri, tra cui Lambert, fecero intravedere brandelli di questo nuovo universo e Gauss lo costruì effettivamente, ma non volle renderlo pubblico. Bolyai, infine, nel 1825 e Lobacevskiy nel 1826, esposero una nuova geometria che partiva dall’assunzione dell’esistenza di due parallele a una data retta. (4)

Bolyai comunicò le sue scoperte al padre commentando: “Aggiungo solo questo: Ho creato un universo completamente nuovo dal nulla.” Il padre invio il lavoro all’amico Gauss che in risposta, dopo aver dichiarato di non aver mai pubblicato nulla sull’argomento per timore delle “strida dei beoti” scrisse “Se inizio dicendo che non posso lodare quest'opera, tu resterai meravigliato per un istante. Ma non posso fare altrimenti, lodarlo sarebbe infatti lodare me stesso; tutto il contenuto dell'opera spianata da tuo figlio coincide quasi interamente con quanto occupa le mie meditazioni da trentacinque anni a questa parte [...] È dunque con gradevole sorpresa che mi viene risparmiata questa fatica [di pubblicare], e sono contento che il figlio di un vecchio amico mi abbia preceduto in modo così notevole”
Le geometrie iperboliche ed ellittiche descrivevano mondi diversi da quello classico. Ma erano mondi o sterili esercitazioni intellettuali per il diletto delle menti matematiche? Per molti geometri il mondo rimaneva euclideo perché nel mondo euclideo si viveva e con la sua geometria si eseguivano misure e calcoli che funzionavano. E poi anche negando Euclide quali delle infinite geometrie ellittiche e iperboliche era quella vera?
Einstein si servì degli strumenti matematici elaborati da Gauss, Riemann, Levi-Civita e Ricci-Curbastro per elaborare la teoria della relatività generale. Nella conferenza di Kyoto del 1922, affermò:

Se tutti i sistemi sono equivalenti allora la geometria euclidea non può valere in ciascuno di essi. Abbandonare la geometria e conservare le leggi fisiche è come descrivere i pensieri senza parole. Bisogna cercare le parole prima di poter esprimere i pensieri. Che cosa si doveva cercare a questo punto? Tale problema rimase insolubile per me fino al 1912, quando all'improvviso mi resi conto che la teoria di Gauss delle superfici forniva la chiave per svelare questo mistero. Compresi che le coordinate di una superficie di Gauss avevano un profondo significato. Non sapevo però a quell'epoca che Riemann aveva studiato i fondamenti della geometria in maniera ancora più profonda. [...] Mi resi conto che i fondamenti della geometria avevano un significato fisico. Quando da Praga tornai a Zurigo, vi trovai il matematico Grossmann, mio caro amico: da lui appresi le prime notizie sul lavoro di Ricci e in seguito su quello di Riemann.

I “nuovi” ed eretici mondi furono accettati dagli accademici con inconsueta calma (o rassegnazione). Ciò accadde perché il problema era ormai maturo e perchè Gauss li approvò con entusiasmo. L’autorità e il genio di Gauss (5) erano così grandi da poter imporre ai dotti custodi dell’ortodossia (pur fra amare masticazioni) anche una simile rivoluzione.
Le implicazioni matematiche, filosofiche, fisiche dell’eresia non euclidea furono enormi e nuove furono tanto l’apertura mentale che lo spirito di libertà che una simile rivoluzione riuscì a suscitare. Com’era effettivamente il mondo? Euclideo o non euclideo? Come si doveva interpretare questa pluralità di geometrie? Come si doveva concepire lo spazio? Le geometrie non euclidea non aprirono solo una porta nei muri dell’ortodossia, ma li sfondarono.
Mentre la geometria veniva così rivoluzionata, l’analisi stava procurando non pochi grattacapi ai suoi adepti. L’elaborazione della neonata teoria delle classi proposta da Cantor procurava più sospetti che certezze. Un’inquietudine che sfociò in una vera guerra che aveva per oggetto la stessa natura degli enti e dei ragionamenti matematici. Quali ragionamenti potevano essere ritenuti sicuri? Quali entità potevano essere accettate? Non fu solo una guerra tra normalizzatori e rivoluzionari. Fu una guerra fra filosofie rivali e fra mentalità irriducibili. Rinviamo per ora lo spinoso problema per affrontarne un altro che paradossalmente nasce dall’aritmetica elementare della cui assiomatizzazione si occupò Peano.

Verità e dimostrazione
A questo punto prima di continuare a girovagare nel modello matematico nato con Pitagora, possiamo affrontare un’importante questione: è possibile limitare la nostra fantasia almeno artificialmente? Almeno in quella matematica ritenuta, a torto o a ragione, la disciplina del rigore?
Si è visto come l’ambigua coincidenza in matematica fra vero e dimostrato, nasce soprattutto dalla trasportabilità analogica su foglio e con essa dall’idealità di numeri e misure. Nasce la dimostrazione su carta come pura operazione di pensiero e, con essa, si fa strada l’identità dimostrabile = vero. Una identità che aveva piena ragion d’essere se si aderiva a una concezione platonica secondo la quale, la verità testimoniava una corrispondenza fra realtà e descrizione linguistica di quella realtà, che per Platone era il puro, perfetto mondo delle idee, un mondo visibile, secondo una metafora di successo, con gli occhi dell’intelletto dopo un’ascesa di una scala di quattro gradini di cui la matematica dimorava al terzo.
Per Aristotele la verità è, dire di ciò che è, che è e, di ciò che non è, che non è. Questa definizione non è in linea di principio diversa da quella di Platone. La ragione del contendere non è nella definizione ma nel separare ciò che è da ciò che non è, che per Platone è separazione tra mondo intellettuale delle idee e apparenza illusoria dei sensi.

Euclide, occupandosi di numeri e di figure non solo unificò il sapere matematico del tempo ma introdusse un’idea rivoluzionaria destinata a mutare, complicare, affinare la concezione della natura della matematica.
Con lui nasce l’assiomatica e, anche se i suoi assiomi vengono giudicati verità evidenti e non convenzionali, (il che non presuppone un mondo platonico ma perlomeno un mondo oggettivo), su di essi viene edificato tutto l’edificio matematico; un edificio che parte dalle fondamenta (assiomi) e si eleva piano dopo piano, teorema dopo teorema.
L’edificio di Euclide si basa:
1) su un certo numero di enunciati (assiomi) presentati come indubitabili, evidenti di per sé,
2) su un certo numero di regole d’inferenza non esplicitamente enunciate che derivano tanto dalla sillogistica aristotelica che dalla logica stoica. Mediante le regole dagli assiomi vengono inferiti i teoremi.
La verità dei teoremi dipende, così, da quella degli assiomi e delle regole d’inferenza. Cambiando gli uni o gli altri, muta l’edificio. Ciò che è vero con un sistema di assiomi e regole può essere falso con un altro sistema. Se si cambia il sistema si cambiano sia il mondo e gli enti che popolano il mondo. Ma qual è il vero mondo e quali i veri enti che popolano il vero mondo? Qual è il criterio con cui dobbiamo avvalorare un mondo e i suoi enti? Nel momento in cui viene messo in dubbio uno dei postulati di Euclide il problema è posto per sempre.
Per molti la risposta sarà la coerenza. Come già riportato, a pagina 66 del suo trattato La scienza e l’ipotesi Poincarè afferma “Mill pretende che ogni definizione contenga un assioma, poiché per definirlo, si afferma implicitamente l’esistenza dell’oggetto definito…..non bisogna dimenticare che la parola ‘esistenza’ non ha lo stesso significato quando si tratta di un essere matematico o quando si tratta di un oggetto materiale. Un essere matematico esiste a condizione che la sua definizione non implichi contraddizione, sia in se stessa, sia con le proposizioni precedentemente ammesse.”
Verità ed esistenza, quindi, subordinate alla coerenza? Ma cosa c’entra la verità con la coerenza?

La coerenza divenne con Hilbert il primo presupposto di verità. Hilbert ritenne indispensabile la dimostrazione della coerenza dell’aritmetica e iniziò un percorso che riconduceva la coerenza di una branca della matematica all’altra. Col suo lavoro sulla geometria non solo dimostrò che se l’aritmetica era coerente allora anche la geometria euclidea lo era ma rivoluzionò la concezione degli enti in assiomatica, rivoluzionando così la stessa assiomatica. Enti ‘primitivi’ come il punto la retta, il piano non venivano più definiti a priori intuitivamente e indipendentemente dagli assiomi ma contestualmente dagli assiomi. Retta, piano, punto divenivano gli enti compatibili e coerenti con gli assiomi. Ovviamente le retta e i piani della geometria euclidea non erano, le rette e i piani delle geometrie ellittiche e iperboliche.

Si fa strada nel pensiero occidentale fino ad emergere con chiarezza l’idea di una molteplicità di forme di verità. Leibniz aveva distinto le verità di ragione dalle verità di fatto. Le verità di fatto esprimerebbero un pensiero che va verificato nell’esperienza (questa tavoletta è rossa) mentre le verità di ragione (Il triangolo rettangolo è un triangolo) sarebbero vere di per sé, in virtù della loro forma. La distinzione pare avvalorata dal fatto che non le verità di ragione ma le verità di fatto ci trasmettono informazioni.
Il Tractatus propose la teoria secondo cui tutte le leggi logiche sono vere in quanto tautologie. L’enunciato “Piove o non piove” è sempre vero perché esprime tutte le possibilità; ma proprio perché esprime tutte le possibilità non ci dice nulla.
Che non ci dica nulla non è certamente vero. Intanto ci dice che esiste la pioggia, poi che a volte può piovere a volte no. Wittgeinstein era tanto consapevole di questo informare da considerare la tautologia l’armatura del mondo. Consideriamo il gioco degli scacchi a cui Wittgenstein amava riferirsi. Un’unica tautologia potrebbe esprimere sotto forma disgiuntiva tutte le possibili prime mosse tutte le possibili prima contromosse e così via. Tutta questa enorme tautologia che esprime tutte le possibili mosse non ci informa con la massima precisione circa le regole e le possibilità del gioco? Non ci dice metaforicamente qual è l’armatura del mondo degli scacchi?
Russell fu subito consapevole dell’importanza della tautologia e suppose che tanto la logica che la matematica si reggessero sulla tautologia. Ramsey ne tentò una presentazione ma il suo tentativo si arenò di fronte all’assioma del’infinito.
Quello di Ramsey fu l’ultimo tentativo realista e logicista di costruzione dell’edificio matematico ma non per questo i matematici cessarono di essere platonici. Come spesso si sente dire, i matematici sono Platonici nei giorni feriali e convenzionalisti la domenica quando parlano coi filosofi ma Goedel era platonico anche la domenica e tentò, come confessa in una lettera, di dimostrare con un teorema matematico la verità del platonismo.
L’abbandono del logicismo platonico significava la resa a una visione assiomatica matematica? Cosa comportava tutto ciò nel rapporto mondi esistenze, verità, dimostrazione, metafora? Lasciamo cadere per ora l’argomento e chiediamoci se un sistema assiomatico riesce, almeno per l’aritmetica, a vincolarci nel mondo standard dei numeri, ossia al mondo di quei numeri che tutti utilizzano ogni giorno per fare i conti della spesa. Chiediamoci in seconda istanza: se si cambia il sistema e si cambiano gli enti, si cambia il mondo? Se sì, qual è il vero mondo e quali sono i veri enti che lo popolano?
Il problema dal nostro punto di vista si può condensare in una domanda: E’ possibile mettere le catene alla nostra fantasia? E’ possibile, ad esempio per la matematica, scrivere delle regole, fissare degli assiomi e, col rigore della formalizzazione, impedirci di scivolare via e, vincolando la nostra fantasia produttiva, mantenerci saldamente ancorati al mondo, entro quei confini che di solito e ambiguamente vengono contrassegnati come di verità? E’ possibile in sostanza, almeno in aritmetica, produrre un sistema di assiomi su cui edificare l’edificio vero delle nostre dimostrazioni senza produrre romanzi (pur rigorosamente formalizzati) di fantascienza?

La prima domanda può assumere dunque la forma: riusciamo con un sistema di assiomi a definire una volta per tutte un mondo coi suoi enti? Rivolgiamo la nostra riflessione ad esempio all’aritmetica elementare. Riusciamo con un sistema di assiomi a caratterizzare il suo mondo e i suoi enti?
Peano cercò di riuscirci e ricostruì la matematica su tre idee primitive (Zero, numero, successore) e sui seguenti cinque postulati:
1. 0 è un numero,
2. il successore di un numero è un numero,
3. due numeri non hanno lo stesso successore,
4. 0 non è il successore di alcun numero,
5. qualsiasi proprietà che appartenga sia a 0 che al successore di qualsiasi numero che la possiede appartiene a tutti i numeri.
Purtroppo i cinque assiomi e i tre concetti primitivi non costituiscono un sistema categorico.
Questo vuol dire il sistema i numeri naturali soddisfa agli assiomi ma anche altre innumerevoli serie (un’infinità) lo soddisfano. In definitiva con quegli assiomi e con quei teoremi non si sa di cosa si parla o, detto in altro modo, la teoria ammette infinite interpretazioni.
Si potrebbe pensare di raggiungere questa categoricità aggiungendo altri assiomi, ma è stato dimostrato che nessun numero finito di assiomi è in grado di raggiungere l’obiettivo; possiamo aggiungere quanti assiomi vogliamo ma non sapremo mai di che serie di oggetti stiamo parlando. Non sapremo mai di che mondo stiamo parlando. Un linguaggio capace di parlare di numeri è e sarà infinitamente ambiguo.
La precisione e la formalizzazione lungi dal chiudere porte e delimitare mondi, ci indicano vie per accedere ad altri. Il mondo dei numeri (ma in generale qualsiasi mondo con qualsiasi sorta di oggetti o individui) non ci sta a essere delimitato e cintato.

Cosa contengono questi mondi non standard, quali balene nuotano nei loro mari di sabbia? Si è parlato dei problemi associati all’invenzione del calcolo infinitesimale, in particolare in relazione a quelle entità indigeste che erano gli infinitesimi, nati come indivisibili che nel mondo geometrico di Bonaventura Cavalieri, che nel mondo della fisica e dell’ingegneria divenivano lamine, movimenti, superfici e volumi elementari. L’Analisi del diciannovesimo secolo soprattutto ad opera di Weierstrass con l’invenzione del concetto di limite, eliminò gli ambigui infinitesimi e rese l’analisi rigorosa, ma tecnici e ingegneri non si conformarono alla riforma avviata attraverso il concetto di limite; una riforma che, come si è detto, elimina dal vocabolario la parola infinitesimo e la concettualità associata. Nei politecnici si è sempre studiato e si studia tutt’ora l’analisi nella sua nuova rigorosa veste, ma in discipline tecniche come la termodinamica l’elettrotecnica, l’idraulica, la meccanica ecc. si continua dopo più di un secolo e mezzo a parlare, dimostrare, ragionare concludere tranquillamente con infinitesimi, con lamine elementari di liquido, con variazioni elementari di campo ecc. come se nulla fosse accaduto.
Lo si fa non perché si contesta o non si accetta la nuova più rigorosa concettualità, ma solo perché il ragionamento procede più speditamente e più intuitivamente e perché il supporre la reale esistenza di queste lamine elementari, di queste variazioni infinitesime, facilità la comprensione.
Dunque tutto procede come se il mondo fosse effettivamente fatto di quella quantità infinitesime di liquido, di solido, di movimento, di energia ecc. anche se fisicamente si conosce non solo la loro insostenibilità fisica ma anche la loro insostenibilità logica.
Eppure si parla del nostro mondo e si va avanti con dimostrazioni e applicazioni come se fosse vero ciò che non lo è. Dimostriamo con dimostrazioni false su ipotesi false e alla fine arriviamo a risultati veri?
Ma di quale mondo, di quale verità parliamo? L’idea di Pitagora che il mondo sia fatto di numeri, che è l’idea di Galileo, che è l’idea che soggiace e nutre molte delle nostre possibilità di comprendere, è tutt’altro che disattiva e morta. E’ stata ed è tuttora così produttiva nella conoscenza e nella trasformazione delle nostre vite da poter considerare nel bene o nel male Pitagora, come Omero, il padre della nostra civiltà . Ma quando entriamo in quei labirinti è il caos.

Il logico americano Robinson dimostrò che esiste un mondo non standard in cui alloggiano oltre i normali numeri che usiamo tutti i giorni anche quei maledetti, benedetti, ambigui, inintelligibili infinitesimi. Non solo: in questa analisi non standard possono essere dimostrati tutti i teoremi dell’analisi tradizionale, come hanno sempre fatto i tecnici e gli ingegneri senza tutta la complicazione dell’apparato epsilon delta. Ma cosa sono questi mondi non standard? (6)
Gli infinitesimi sono le sarde del deserto di sabbia? Anche qui entriamo in un mondo immaginario fatto (metaforicamente) di un’altra pasta per poi rientrare nel nostro. Come si configura il rapporto tra vero per dimostrazione, vero in sé stesso, sempre vero? Come si rapporta il dimostrabile col vero?

I mondi non standard.
In ogni caso i mondi non standard sono la testimonianza della impossibilità d’incatenare gli oggetti e gli ambienti di una teoria a un mondo, (al nostro mondo) e dell’impossibilità di vietare l’evasione verso altri universi: una pluralità di mondi e di abitanti di quei mondi non standard, che marcano la loro alienità rispetto alla realizzazione standard più usuale, e aprono vie insospettate verso l’insolito e l’immaginario.
Ci chiediamo quali siano le vie per liberarsi dalle catene e la storia della geometria non euclidea già ci da una risposta. La modifica dell’assioma delle parallele generò, oltre al mondo euclideo, mondi ellittici e mondi iperbolici altrettanto coerenti con l’aritmetica e altrettanto interessanti. Mondi in cui la verità veniva sballottata e relativizzata. Ciò che era vero in un mondo poteva essere falso in un altro. Mondi così diversi da quello standard euclideo da poter essere considerati alieni.
La scoperta di Goedel di proposizioni indecidibili apriva un ulteriore falla nelle illusioni di contenimento.
Se, infatti, una proposizione a è indecidibile in una teoria coerente K , a è indipendente dagli assiomi di K e può essere quindi aggiunto agli altri assiomi di K per formare un’altra teoria K1 anch’essa coerente ma differente da K. Inoltre se a è la nostra proposizione indecidibile anche la negazione di a lo è ed ecco che abbiamo un’ulteriore teoria K2 diversa da K e da K1.
A loro volta anche K1 e K2 avranno proposizione indecidibili e così. Il processo di moltiplicazione delle teorie non ha fine. Si apre quindi altri accessi a infinità di mondi non standard.

Perchè questo breve escursus? Per tanti motivi. Innanzitutto per introdurre un discorso per:
1) parlare della capacità delle teorie formalizzate di definire individui e mondi,
2) gettar sospetti sulla natura degli enti matematici,
3) insinuare non in maniera generica che il campo delle metafore è molto più vasto e profondo di quanto si crede.

Cos’è la matematica? É riducibile alla logica e alla teoria degli insiemi come ritenevano Frege e Russell? È un sistema formale come riteneva Hilbert? Un mero insieme di regole circa segni tracciati sulla carta a cui è possibile dare un senso solo uscendo dalla matematica per salire a un piano superiore? Oppure un tentativo di coprire il mondo dandone un modello, che una volta impostato cammina per suo conto e dalla progettata copertura analogica passa alla metafora, dal mare di sabbia alle balene della sabbia?

Coerenza
Neppure la coerenza è immune da dubbi.
La coerenza diventa con Hilbert il concetto base dell’edificio matematico. Criterio di esistenza e di verità.’ Non possiamo evadere dalla coerenza? Non si danno mondi non coerenti? Certamente non solo esistono ma sono davanti ai nostri occhi tutti i giorni. Limitiamoci a considerare che nel mondo sociale un comportamento coerente è spesso considerato ideologico e ottuso. Se dovessimo mantenere coerente il nostro comportamento (le nostre idee, ecc) non potremmo mai cambiare opinione. Non potremmo riconoscere gli errori. Non ci sarebbero né scienza, né mutamento né democrazia. L’uomo che è vissuto e sopravvissuto così com’è perché ha saputo riconoscere e prendere coscienza dei propri errori. Ma anche la coerenza ‘orizzontale’ sarebbe inconcepibile. La nostra società è formata da tanti mondi, credi religiosi, istituzioni, associazioni ecc. ciascuna con le sue regole di verità. Sarebbe assurdo, illegale, antidemocratico esigere la conservazione a tutti i costi della coerenza in chiesa, a scuola, nella vita democratica, in tribunale.
Detto ciò, dobbiamo constatare che anche dogmi di fede cristiana come quello della trinità, sono contradditori, ma non per questo i fedeli cessano di credere, che in fisica il doppio stato corpuscolare e ondulatoria della luce è altrettanto incoerente, con l’aggravante che per la fisica, fondata sui principi logici e matematici, un simile stato di cose è intollerabile. In ogni caso, pur intollerabile. viene accettato in attesa che una teoria più articolata possa eliminare le contraddizioni (ammesso che sia un giorno possibile). Anche l’atomo di Bohr non era certo un modello di coerenza ma non per questo venne buttato nel cestino. Anche i nostri mondi di favole e di fantascienza rivelano incoerenze ma non per questo smettiamo di leggerli.

Potremmo dire e potremmo ancora fare molti altri esempi ma ciò non toglie che il problema della coerenza continui a preoccupare logici, matematici e pensatori. Perché in una favola la coerenza può non preoccuparci e in logica sì? Potremmo rispondere che esiste un teorema di logica (di Scoto) secondo il quale da una contraddizione derivano sia tutte le proposizioni che le loro negazioni ma altrettanto potremmo constatare che, se facciamo finta che il teorema di Scoto non esista, logica e matematica continuano tranquillamente a fare la loro funzione.
Molti matematici, in effetti, non si curano del teorema di Scoto e continuano a far matematica. Molti ma non tutti. Hilbert, giudicando la situazione generata dalle antinomie intollerabile, pose tra i problemi fondamentali proprio quello della coerenza della matematica.
Ma anche per la matematica - anzi sempre per mantenerci ai livelli più semplici- l’aritmetica di Peano sorgono problemi. E mica problemi da poco visto che neppure per l’aritmetica di Peano si può dimostrare la coerenza con metodi finitari. Una frase infelice che andrebbe riformulata come. E’ dimostrato che la coerenza dell’aritmetica di Peano è indimostrabile con metodi finitari. Il termine ‘finitario’ è ambiguo anche per i matematici ma questo non deve impressionare perché non si è molto lontani dal vero considerando finitari tutti i tipi di ragionamento accettati dalla pressoché totalità degli addetti ai lavori.
Nel 1941 Skolem scopre un teorema paradossale che recita: se un sistema di espressioni possiede un modello esso ne possiede anche uno numerabile. Un esempio di conseguenza di questo sistema è che, a meno che la teoria ZF(7 )sia contraddittoria, l’insieme potenza dell’insieme dei numeri naturali contemporaneamente è e non è numerabile.
Lo stesso Skolem fornì un’interpretazione nello stesso tempo tranquillizzante e inquietante del paradosso; tranquillizzante perchè non è una nuova antinomia, inquietante perchè il paradosso si può interpretare come se nel linguaggio della teoria degli insiemi si dimostrasse la non esistenza di un certo insieme di cui dimostriamo l’esistenza nel metalinguaggio. Il che è come dire che esistenza o non esistenza di un insieme non è assoluta, ma dipende dal linguaggio con cui ne parliamo. Con un linguaggio possiamo affermare ciò che con un altro neghiamo.
In effetti, non pochi interpretarono il paradosso come la condanna del platonismo matematico. Il mondo dei concetti, delle teorie, delle parole irrompe in una realtà che, come dice Borges, “anelava a cedere”.
Nel 1930 Goedel comunicò due inquietanti scoperte. La prima afferma che la coerenza di un sistema comprendente la teoria dei numeri non può essere dimostrata (Weyl commentò che Dio esiste perchè la matematica e coerente e il diavolo pure perchè questa coerenza non può essere dimostrata), la seconda che una qualsiasi teoria se è coerente e comprende il sistema dei numeri, ha almeno un enunciato vero e non dimostrabile.
Ma perché tanta insistenza sulla coerenza? Il problema della coerenza si infiammò di colpo con la scoperta delle antinomie e su questi veri, disastrosi, autentici buchi neri della coerenza e della verità non si può più rimandare il discorso.

Le antinomie e i rimedi autocontradditori
Quando le antinomie misero in crisi le costruzione di Frege e di Cantor, le reazioni furono varie. Poincarè le addebitò all’infinito attuale dei cantoriani e alle definizioni impredicative: definizioni vere per i matematici platonici ma problematiche per chi platonico non è.
Russell edificò nei Principia un complesso palazzo a infiniti piani generati da infinite gerarchie di tipi (ontologici) e ordini (concettuali) che non potevano essere mescolate. Ma i Principia introducevano un principio, quello di riducibilità, estraneo alla logica e non riuscivano a introdurre il principio dell’Infinito se non assumendo l’ipotesi del tutto metafisica dell’esistenza di infiniti oggetti.
Nel 1908 lo stesso anno in cui Principia presentò quella che Wittgeinstein chiamava la “bestiale teoria dei tipi”, Zermelo propose una soluzione assiomatica, e Brower una dottrina intuizionista. A Ramsey si deve la suddivisione delle antinomie in antinomie linguistiche e matematiche. Tarsky, un anno dopo i teoremi limitativi di Goedel, invitò a risolvere le prime con metodi semantici formalizzati che prevedevano una gerarchia di linguaggi e di verità.
Tutte queste soluzioni prevedono gerarchie indefinitamente estese verso l’alto (anche la teoria assiomatica di Zermelo - è stato notato - prevede una gerarchie di ranghi). In particolare quella di Tarsky che stabiliva che ciascun linguaggio dovesse delegare la sua verità di gradino in gradino senza mai raggiungere un ultimo piano capace di autoveritarsi. Se gli assiomi non sono evidenti, se la verità si scarica sempre a livelli successivi come si può parlare di verità?
E’ vero che Tarsky parla dei linguaggi formalizzati e non del linguaggio naturale, è vero che riesce in tal modo a stabilire una netta separazione fra strutture sintattiche e strutture semantiche che le realizzano ma già la pluralità di realizzazioni per ogni struttura sintattica ci apre verso una pluralità di mondi in cui la verità è relativizzata alla realizzazione. Per gli scolastici la verità era adaequatio rei et intellectus ma che facciamo se manca la res o se la res è multipla?
La teoria sulla verità di Tarsky poté e può sembrare una brillante soluzione come, a suo tempo, poté era sembrata brillante la teoria dei tipi e degli ordini di Russell ma tutte queste soluzioni hanno una struttura che rinvia gerarchicamente a un nuovo tipo, a un nuovo ordine, a un nuovo linguaggio in una ascesa senza fine.
Non è un problema nuovo in filosofia.
Chi muove una cosa? Un’altra cosa dotata di motore? E chi muove il motore di quella cosa? Un altro motore. E chi muove quel motore?
Chi ha creato il mondo? Dio creatore. E chi ha creato il dio creatore?
Perché il male? Perchè è mancanza di bene. E perché è mancanza di bene?
Anche Aristotele e Tommaso delegavano verso l’alto ma affinché la delega non fosse infinita e inconcludente dovevano bloccare l’infernale meccanismo con entità divine, illogiche e autocontradditorie come il motore immobile e il dio creante e increato. Così nei processi: il giudice giudica ma chi giudica il giudice sul giudizio? Un altro giudice? E chi l’altro giudice? Ovunque c’è giudizio, selezione, scelta nasce l’ascesa che si può troncare soltanto col giudice ingiudicabile che giudica se stesso sul giudizio. Questioni di questo tipo si risolvono nella prassi ma non in via teorica, dove il problema di principio rimane: le antinomie, per essere risolte, richiedono gerarchizzazioni infinite inaccettabili. Per troncarle riproduciamo antinomie o contraddizioni.

Coerenza della coerenza
Il concetto stesso di coerenza non sfugge al meccanismo perverso. Per dimostrare la coerenza della geometria dimostriamo non la sua coerenza assoluta ma la sua coerenza relativa all’aritmetica, che ci consente di dire che la geometria è coerente solo se l’aritmetica è coerente. Se vogliamo dimostrare la coerenza dell’aritmetica di Peano cerchiamo di dimostrarne la coerenza relativa, ad esempio, al sistema di Zermelo. Che significa tutto ciò se non che anche la coerenza è avviata verso un altro regresso all’infinito? Che possiamo fare per fermare questo meccanismo diabolico se non ricorrere alla auto coerenza indimostrabile?
Sappiamo, infatti, che se l’aritmetica di Peano è coerente allora è dimostrato che non può dimostrare la propria coerenza. Se chiamiamo COE la stringa finale di questa dimostrazione, allora COE è indecidibile. Ma se è indecidibile allora possiamo aggiungere senza problemi la negazione di COE come assioma, ottenendo un nuovo sistema che dichiara l’incoerenza di COE.

Si legge spesso che le antinomie sono ed erano un problema per i logici e per i filosofi della matematica ma non per i matematici. Questo è solo parzialmente vero. E’ vero che le antinomie non disturbavano né intralciavano l’operare dei matematici nei loro calcoli e nelle loro ricerche, come ebbe a pronunciarsi anche Goedel, ma è altrettanto vero che accanto a Russell, Frege, Couturat, che erano logici e non matematici, altri matematici come Hilbert, Brouwer, Herman Weill considerarono strutturali i problemi sollevati dalle antinomie. Anche Poincarè non si sottrasse alla polemica. E proprio le tesi di Poincare (vedi la sua condanna delle finizioni impredicative e delle teorie cantoriane) ci mostrano, se mai c’era stata necessità, che i problemi non erano affatto limitati alle antinomie ma riguardavano in generale la natura della matematica, degli enti e dei ragionamenti ammissibili.
Ma in che senso disturbano o non disturbano i matematici? Che non li disturbino è evidente. Sia coloro usano l’aritmetica per calcoli commerciali o per contabilità domestica, sia coloro che la usano per la ricerca, continuano, come ha sempre fatto con successo, il loro operare matematico senza essere minimamente disturbato dalle antinomie. Il senso di fallimento che colpì Frege, quando venne informato da Russell circa la scoperta dell’antinomia che porta il suo nome e che lo indusse a pensare che tutto l’edificio matematico stesse crollando, non li tocca minimamente. Al massimo possono pensare che ciò che crolla non è la matematica ma quella barocca costruzione con cui Frege pensava di fondare la matematica.
E’ poi così importante fondere in un’unica costruzione matematica, logica e teoria degli insiemi? Il sistema di Zermelo sembra raggiungere l’obiettivo senza incappare nelle antinomie, ma servono a qualcosa tanta fatica e tanta complicazione? E per ottenere cosa? In definitiva sembra il mondo dei numeri e la sua manipolazione possa fare a meno degli insiemi come teoria fondante dell’aritmetica. Oltretutto non è insensato cercare di fondare il mondo dei numeri su quello degli insiemi quando il concetto di insieme sembra più nebuloso di quello di numero?
Di nuovo dobbiamo dire che le cose sono più complesse, che non tutti i problemi sono risolubili con un colpo di spada come fece Alessandro col nodo di Gordio.

Con le antinomie sembra che non solo si sia giunti a un qualche limite d’espressività e di dimostrabilità ma ai limiti di un universo concettuale che offre scappatoie oltre le quali ci siano solo abissi e labirinti. Un limite comunque relativo che possiamo sempre ampliare aggiungendo tipi di ragionamento e entità per giungere, però, con l’ampliamento, ad analoghi problemi. A questo punto non resta che appellarci ad antiche nomenclature di auto evidenza, di prassi, di utilità, di funzionalità, di certezza intuitiva rinunciando alla dimostrazione.

Antinomie e rimedi paradigma verticale
L’angoscia (8) della domanda non è solo linguistica ma propria del paradigma verticale vincente.
La domanda: “Dio ha creato noi chi ha creato dio?” è con parole diverse la stessa di Heidegger: “Perché l’essere e non il nulla?”
Ma è il paradigma verticale vincente, un paradigma che ci costituisce, a portarci l’angoscia. Noi possiamo porre fine alla catena con la causa incausata ma non è questo uno dei tanti artifici autocontradditori del paradigma per placare l’angoscia? Perché la violazione della coerenza non ce la rinnova, rinnovando ciò che chiamiamo ‘mistero’? (9) Come ci poniamo verso questo mistero? Riponiamo lì il senso complessivo della nostra vita?
Nel nostro paradigma linguistico è naturale dare il nome alle cose di cui vogliamo parlare. Ma il ‘mistero’ è un oggetto, un organizzazione, una struttura? Non lo sappiamo ovviamente noi diamo nome anche ai limiti, ai confini fra dicibile e indicibile, al referenziale e al non referenziale, anche se termini come referenziale, senso, ecc. hanno significati plurimi e non esplicitamente condivisi. Potremmo al posto di mistero dire: “Ciò di cui non si sa nulla e che c’inquieta” Ma non diciamo già qualcosa di troppo con quel ‘ciò’? Esiste quel ‘ciò’? Se è una variabile per indicare qualcosa che non conosciamo; non si sa neppure in quale universo vari la variabile. Addirittura sentiamo che il mistero non è qualcosa che possiamo svelare ma un qualcosa di insvelabile.
Se le cose stanno così, ci troviamo alle prese con l’uso improprio di un nome per indicare un limite. Col nostro linguaggio, col nostro paradigma d’interpretazione non siamo in gradi di spingere oltre l’indagine. Riprenderemo l’argomento parlando del linguaggio.

Antinomie, paradossi
Siamo nelle stesse condizioni di chi si propose di riprodurre su carta, ossia su una superficie piana, la superficie sferica del mondo.
Proiettando dalla sfera su un piano tangente al polo lungo rette parallele si ottengono rappresentazioni piane verosimili nelle vicinanze del polo e sempre più false man mano che ci si allontana.
Non diversamente nel linguaggio man mano che ci inoltriamo verso l’esterno, man mano che abbandoniamo l’avvenuto convergere delle lingua sul mondo, degli oggetti sui nomi e delle proposizioni sui fatti e ci inoltriamo oltre e dentro questa convergenza, ci addentriamo in confini che sono la stessa descrizione del linguaggio e del suo funzionamento, inciampiamo nei paradossi di un linguaggio che non riesce a seguire il mondo e si perde nell’eternità di un numero di una diagonale, di un Achille inseguitore di una tartaruga, di in cretese bugiardo, di una classe di tutte le classi impropria se propria e propria se impropria. E questo non sono che le punte storiche. Come se avessimo eretto, per superare gli scogli, meravigliosi castelli in cui però né i numeri né la logica né i concetti né il linguaggio riescono ad abitare a meno di rinunciare ad essere ciò che sono o a meno di accogliere in quel castello altri infiniti castelli denominati significativamente ‘non standard’ i cui abitanti sono infiniti e sorprendenti. E’ il limite invalicabile del paradigma verticale che pur ha avuto tanto successo nella nostra evoluzione.

Antinomie verità
Si dice che l’antinomia è solo un incidente ai confini; un incidente di cui possiamo non prenderci cura come fanno tanti matematici. C’è un’antinomia? Lasciamola in pace, teniamoci lontani. Lo stesso raccomandava Wittgenstein che riteneva la filosofia una malattia, una chiacchiera di s’ammalano ostinatamente i filosofi. Un ostinarsi che di per sé, al di là di non portare da nessuna parte, non danneggerebbe nessuno se non intralciasse con la chiacchiera e la presunzione quei matematici che fanno matematica e non chiacchiera matematica.

Ma si può dire che le antinomie sono in periferia, e basta guardare dove si mettono i piedi?
Altre considerazioni spingono in questo senso. Dato un sistema assiomatico che fonda una teoria è probabile che esistano altri sistemi assiomatici in cui ciò che è assioma in un sistema è teorema in un altro e viceversa. A questo punto dov’è il centro, dov’è la periferia, dove l’edificio, dove le fondazioni?
C’è poi il teorema di Scoto che invalida tutta una teoria che genera una contraddizione poiché ci dice che una teoria affetta da morbo antinominico accetta tutte le proposizioni e le loro negazioni. Ma sono veramente invalidate logica e insiemistica dal teorema di Scoto? Evidentemente no, se basta non utilizzare l’antinomia. Se così fosse non riusciremmo neppure a parlarci.
Gran parte dei matematici, dei ricercatori, dei geometri, dei ragionieri non sanno che esistono antinomie né che esiste il teorema di Scoto e, anche se lo sapessero, continuerebbero tranquillamente a praticare i loro calcoli senza porsi problemi se siano fondati o no. Grandi matematici come Poincarè non sopportavano neppure l’idea di una formalizzazione. Lo stesso Goedel ebbe a puntualizzare che nella pratica matematica non esistevano quei problemi.
L’atteggiamento di questi matematici praticanti e diffidenti verso ogni assolutismo-fondazionismo matematico inventò e praticò una filosofia senza fondamenti assai prima che gli ermeneutici sulle orme di Nietzsche e Heidegger la proclamassero.

Si potrebbe rispondere con Hilbert che una matematica incoerente non è assolutamente accettabile. Si può aggiungere che il rigore e la coerenza naturalmente devono valere per le regole con cui si manipolano le proposizioni e per gli enti che si introducono, ma tutto ciò non implica che il concetto di coerenza e di forma diventino fondanti? Per cosa? Per la verità? Su cosa possiamo giudicare sui tipi di inferenza visto che ad esempio l’eresia intuizionista ha gettato dubbi sul principio del terzo escluso, sulla doppia negazione, sullo stesso procedere in matematica?
Non è meglio rinunciare all’edifico compatto coerente che tutto abbraccia senza nulla tralasciare? E le antinomie e i falsi rimedi per le antinomie illusori o addirittura contradditori come la causa incausata, il motore immobile?
Il sistema di Russell con la sua moltiplicazione di enti, di numeri, di gradini complicava enormemente un edifico senza portare vantaggi ai matematici alle prese con veri, autentici problemi matematici.
J. R. Weinberg nella sua Introduzione al Positivismo Logico (1950 Einaudi) condensò in tre punti i difetti dei Principia: esprimevano 1) troppa teoria, 2) non sufficiente teoria, 3) assoluta mancanza di teoria. Questi non sono solo i difetti di Principia ma di tutto il paradigma verticale e del linguaggio in cui il paradigma si articola.
Da una parte Principia si presentava, sì, come un sistema formale espresso in linguaggio formale ma doveva essere spiegato ad ogni passo con istruzioni espresse nel linguaggio comune. Una teoria, che richiede un linguaggio non formalizzato, non testimonia un deficit di teoria e contemporaneamente un eccesso di teoria?
Il sistema di Russell come tutti i sistemi formalizzati siano essi logicisti o formalisti hanno in definitiva necessità di essere illustrati spiegati, introdotti dall’imperfetto, impreciso, non formalizzato linguaggio comune. Una fondazione fragile per un palazzo robusto. Il certo fondato sull’incerto, il preciso sul confuso.
Ma le cosa stanno veramente così? Per ora limitiamoci a rilevare che lo studio dei linguaggi formalizzati della loro sintassi e semantica fornisce strumenti per migliorare l’espressività del linguaggio comune indirizzandolo in definitiva verso uno statuto logico che da un lato tende a esprimersi con rigore e dall’altra a mantenere una capacità esplicativa e quel tipo di significatività che lo rende comprensibile come linguaggio comune. Questo naturalmente nelle intenzioni. E’ comunque indubbio che un’analisi del linguaggio comune spinge in questo senso e che gli studi linguistici non possono che risultare utili strumenti di chiarificazione. Altrettanto evidente è il continuo movimento circolare dal linguaggio comune a quello formalizzato e viceversa.

Verità coi numeri
Ha senso chiedersi se si può parlare di verità o falsità aritmetiche? Ha senso ampliare la domanda su cosa sia la verità e la falsità? Forse l’idea che verità e falsità abbiano oggettivamente una molteplicità di significati al variare dell’ambiente, della teoria, della concettualità, è la più adeguata. L’idea di verità come un abitare, un essere cambiati dalla verità in un esperienza estetica, ad esempio guardando un quadro, leggendo un racconto così come proposto dai seguaci di Heidegger e Gadamer coglie qualcosa di importante, ma non è certo esauriente: tante sono le esperienze estetiche e non estetiche che possono cambiarci. Ma ciò a cui siamo indotti a pensare in riferimento al comune sentire la verità non è altrettanto plurisignificante.
Tarski nella sua ricerca volle richiamarsi ad Aristotele e significare che la verità è dire di ciò che è vero, che è vero, e di ciò che è falso che è falso. Cosi “La neve è bianca” è vero se la neve è bianca dove il primo enunciato “La neve è bianca” è citato fra virgolette come puro susseguirsi di gruppi di lettere per cui potremmo tradurre “l’enunciato formato dal termine ‘la’ seguito dal termine ‘neve’ seguito ecc. ecc.” è vero se la neve è bianca.
Una prima osservazione e un primo dubbio.
Da una parte abbiamo una realtà empirica di cui abbiamo esperienza dall’altra l’enunciato“la neve è bianca” la verità scaturisce dal confronto della realtà con l’enunciato; se c’è corrispondenza diciamo che l’enunciato è vero se non c’è diciamo che è falso. Ma nel caso di un enunciato sui numeri fra quali due entità avviene il paragone che consente di parlare di verità o falsità? E’ chiaro che non esiste una realtà dei numeri nelle stesse modalità con cui esistono la neve e il colore bianco.
Possiamo dire che “La neve è bianca” è vera o falsa soltanto se ne comprendiamo il significato. Lo stesso per l’enunciato “5 + 1 = 6”.
Se ammettiamo con Goedel e col primo Russell un’esistenza platonica dei numeri è chiaro che i due termini di confronto ci sono. Se ammettiamo che le origini delle verità matematiche sono empiriche con Stuart Mill anche in questo caso i termini di confronto ci sono. Ma se la nostra impostazione è assiomatica, concettualista o intuizionista?
In ogni caso da una parte l’enunciato linguistico dall’altro la realtà, da una parte la struttura sintattica in cui si può parlare di decidibilità, di dimostrazione, ma non di verità. dall’altro la ‘realizzazione’ nel senso di Tarski in cui può parlare di verità. Una struttura sintattica molte possibili realizzazioni, in ognuna delle quali un enunciato della struttura può ‘realizzarsi’ come vero o come falso.

---

Note:
1) Un sospetto che durò almeno due secoli fino a che Cauchy e Weierstrass non inventarono una procedura che otteneva gli stessi risultati, ma non parlava di infinitesimi. L’analisi poté essere trascritta e redenta dal rigore che il nuovo metodo permetteva.
Nella seconda metà di questo secolo, quegli stessi infinitesimi, che secondo Leibniz costituivano la grana fine dell’universo accessibile solo all’intelligenza infinita di Dio, si presero la rivincita, divenendo legittimi e non eretici cittadini nei mondi dell’analisi non standard inventata ( o scoperta o costruita, o fondata) da Robinson.
2) Mach 1872, p.31. La citazione proviene da un articolo di A. G. Gargani contenuto in Filosofia ’90 a cura di G. Vattimo.
3) Uso “assioma” anche per i postulati.
4)
5) Gauss non doveva credere certamente alla sua autorità se, avendo lui stesso elaborato una geometria non euclidea (nel senso di Boylay), non la pubblicò perchè, come ebbe a dire, temeva le urla dei beoti.
6) Potremmo benissimo chiamarli immaginari o veri, perché non esiste alcuna base che ci garantisca una qualsiasi forma di preminenza del mondo cosiddetto Standard rispetto ai mondi denominati Non Standard: semplicemente per convenzione e per abitudine il mondo Standard è quello usuale, quello a cui siamo abituati, quello che è sempre stato considerato in una qualche maniera quello ‘vero’
7) Sistema assiomatico per la teoria degli insiemi.
8) Vedi appendice sul concetto di destino.
9) È in parte l’argomento trattato nel capitolo delle parole vaghe.

---

ES - 27 marzo 2013

---