Acceleration is a vector, it is the rate at which velocity changes; as in previous cases, average acceleration and instantaneous acceleration usually differ from each other.
Average acceleration
Average acceleration is the change in velocity over the time elapsed to
produce that change:
where
is called the "change in velocity vector".
The magnitude of the average acceleration vector is equal to the change in
speed over the time elapsed
.
The direction of
is equal to the direction of 
.
Example: The car in the figure below, overshoots point A with a velocity 
=30m/s(108km/h)
at the instant 
=0sec. Then,
after 5 seconds, it overshoots point B with a velocity 
=10m/s(36km/h).
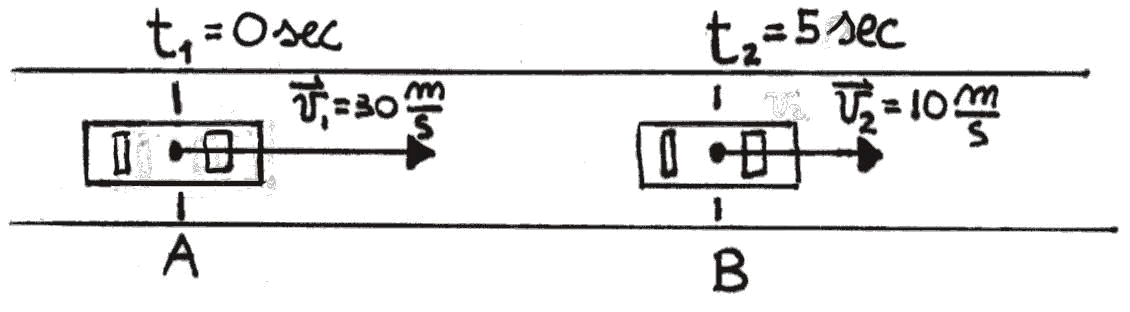
The velocity is changed, it has decreased, this means that negative acceleration
took place. Its magnitude is
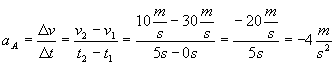
Notice that the unit of measurement of acceleration is meters per second
squared.
The direction is the same as 
:
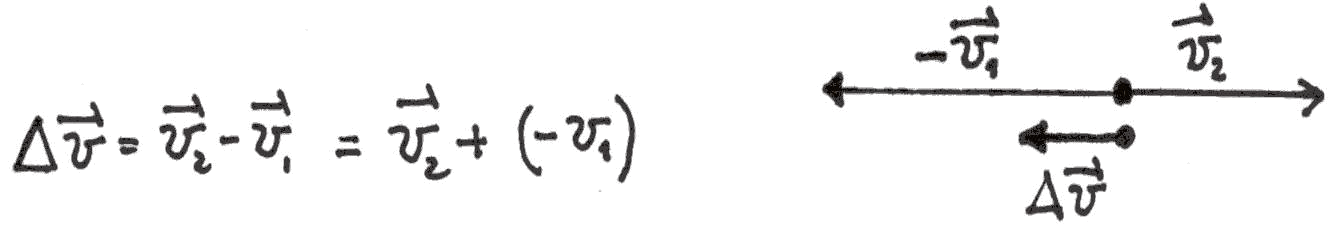
This means that the acceleration is leftward oriented as the 
vector
is. In effect in this example, the acceleration opposes the movement.
Another example concerning the direction of the acceleration is the one in the
figure below:
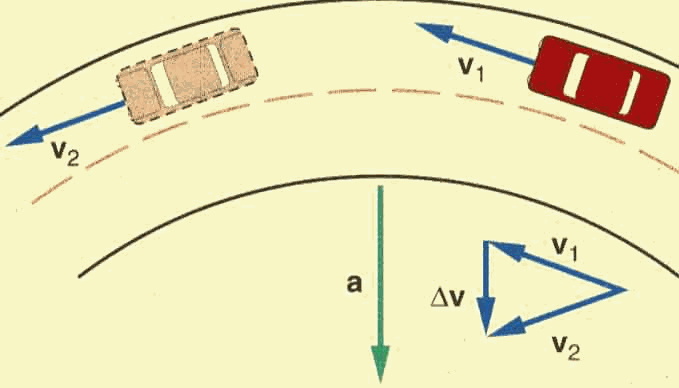
A car is describing a circular motion with a constant speed. The speed is
constant but the direction of the velocity changes over time, hence acceleration
exists!
What is the direction of this acceleration? The answer is always the same: the
direction of the acceleration is the same as ,
and it is directed towards the centre of the curve, as demonstrated by the
parallelogram rule in the diagram below:
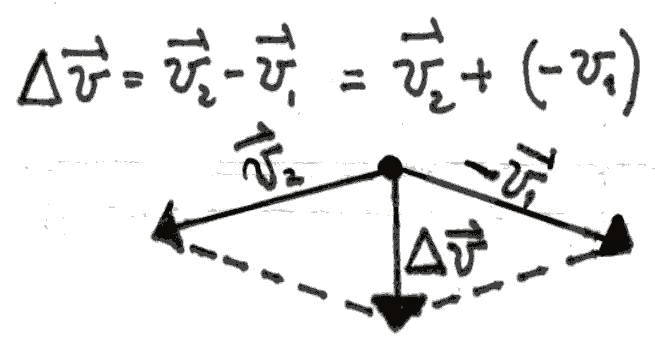
An object having a constant speed in a circular motion is subjected to an
acceleration that changes its direction at every instant. This acceleration
always points towards the centre of the curve!
Instantaneous acceleration 
To treat problems in which acceleration changes at every instant, it is
useful to introduce the idea of instantaneous acceleration. Instantaneous
acceleration is computed by finding the average acceleration for a very short
interval of time:
As for instantaneous velocity, in general instantaneous acceleration is a
function of time
and differs from average acceleration.
The two quantities are equal only when the acceleration is constant during the
whole motion.
In this special case it is possible to write that 
.
| Next | Index |