Graphing motion.

All the quantities involved in the description of motion (time, distance, velocity and acceleration) can be resumed by using diagrams and the rules of analytic geometry. As a matter of fact, a graph is the best way to deduce qualitative but precise information about motion. An analysis of the following example will illustrate this idea.
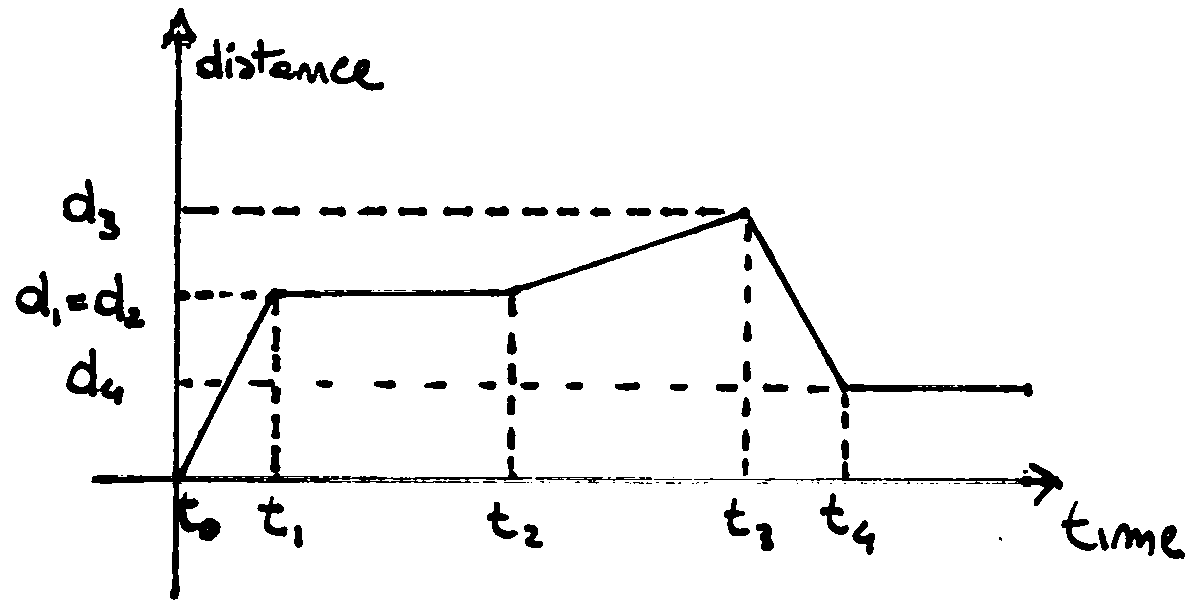
Suppose that an object moves, and its motion is recorded on the following distance-time graph:

The graph reveals considerable information about the motion.
Between and (), the object has a positive constant velocity: as a matter of fact its position passes from to [the dotted tangent to the graph has a positive slope];
between and (), the object is at rest. It has no velocity: as time passes its position doesn’t change [the tangent line has no slope, the slope is equal to zero];
between and (), the object moves again and its position passes from = to ; now its velocity is positive again, but it is smaller than before: a longer interval of time is needed to cover a shorter distance [the tangent line has a positive slope but it is less steep than before];
between and (), the object turns back and its velocity becomes negative: as time passes the position is reduced until [the tangent line has a negative slope];
At the point the object stops short, then it remains at rest [the tangent line has no slope again].
Hence it is possible to deduce the velocity by looking at the slope of the distance versus time graph. To be more precise, the instantaneous velocity at a given instant is the angular coefficient of the straight line tangents to the distance versus time graph at that instant.

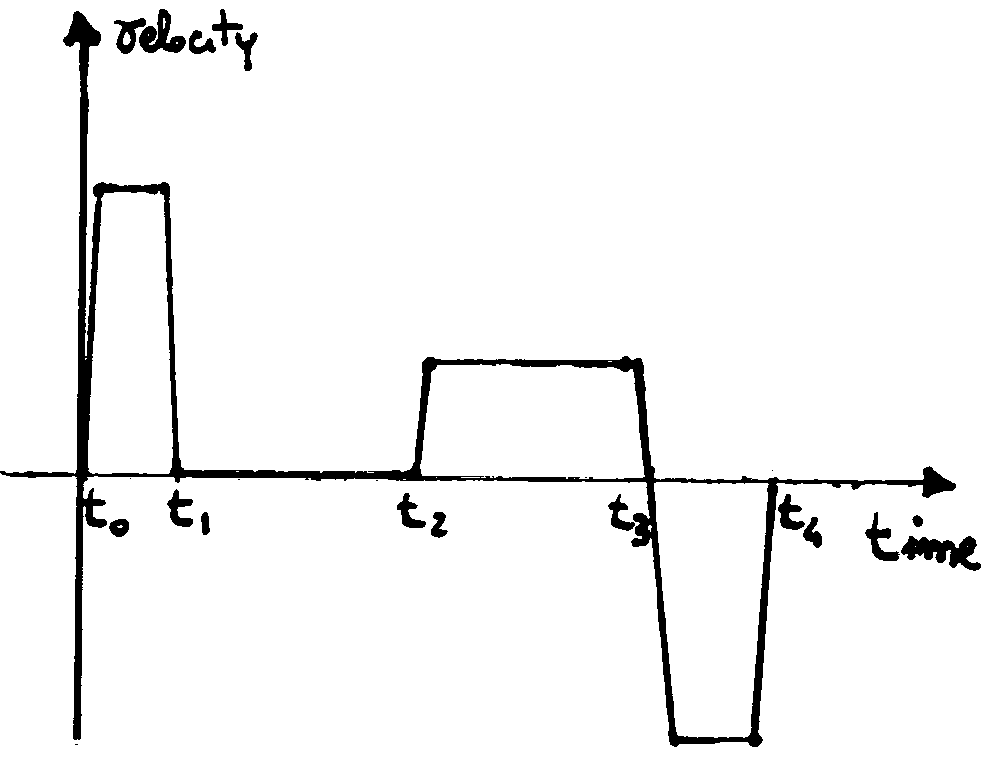
Apart from the initial instant, during which a strong acceleration takes place, the object spends the major part of the period between and () with a constant velocity, and its acceleration is zero (no slope). Then, at approximately , the object brakes suddenly: a negative acceleration takes place (negative slope of the tangent line).
Between and (), the velocity is zero and acceleration is zero too.
At the instant a new and positive acceleration lets the object pass from resting to a new constant velocity, and so on…
With a similar argument as before, the acceleration can be deduced by looking at the velocity versus time graph: the instantaneous acceleration at a given instant is the angular coefficient of the straight line tangents to the velocity versus time graph at that instant.

Every time the velocity changes, a spike of acceleration appears in order to justify that change. The acceleration is positive when the change in velocity give rises to a larger velocity and vice-versa, it is negative when the velocity changes to a smaller magnitude.
Notice that the described motion is quite complex because the acceleration varies over time. All the motions where a varying acceleration takes place, will be treated in our course from the qualitative point of view only. We will try to describe mathematically only easier motions, like the uniform velocity motion or the uniform acceleration motion.