Average speed
The average speed is the first concept we find in Kinematics.
Average speed of a moving object is defined as the ratio between the distance
travelled by the object and the interval of time required to cover that
distance.
It can be stated simply by saying that:
Average speed is the distance travelled divided by the time elapsed.
Another way to define it, is by using the word "rate":
Average speed is the rate at which distance is covered over time.
In mathematical language we write:
where
and
In the SI, the unit of measurement of speed is the unit of distance over the
unit of time, hence 
.
Example: What is the average velocity of the car in the figure below during the
interval that the clock reading changes from 10 to 25 seconds?
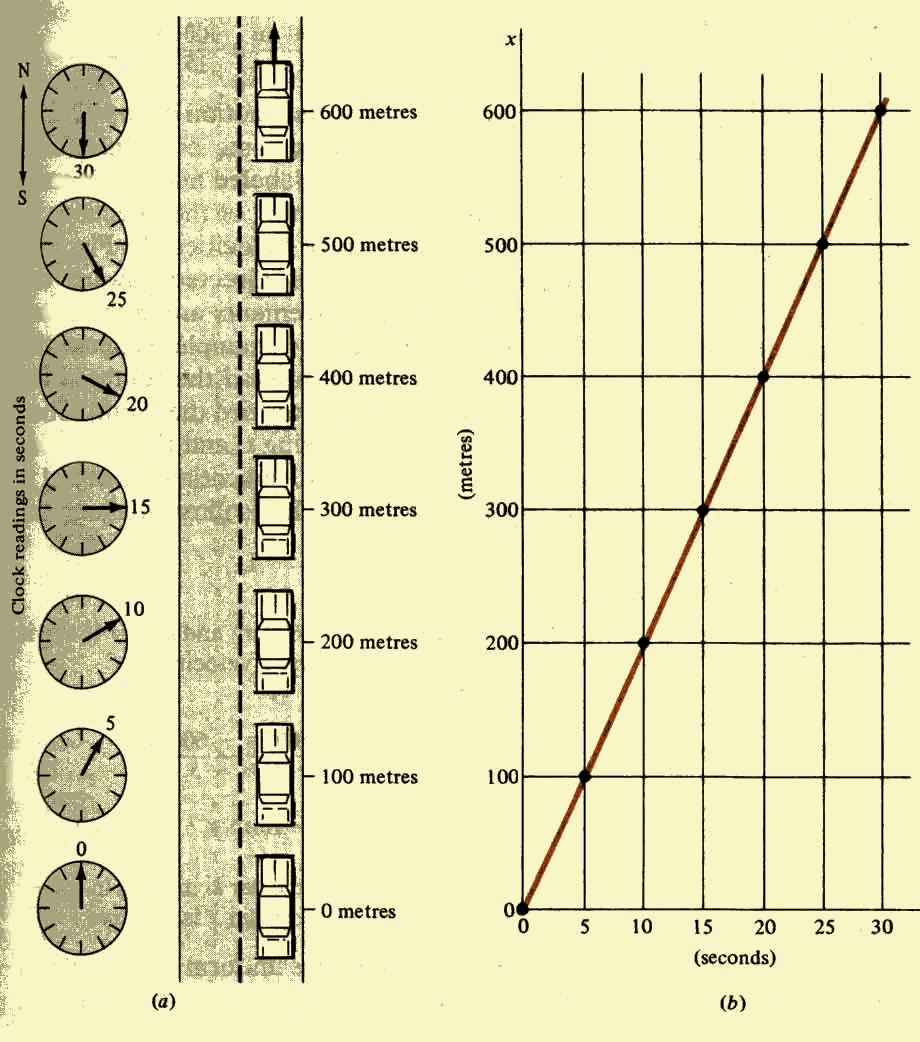
From the figure, we see that the car travels a distance
during a period of time
,
hence, the average velocity of the car is
.
Instantaneous speed 
Instantaneous speed of a moving object is the speed the object has at a given
instant in time; it’s the rate at which distance is covered at a given instant
in time. Usually it differs from average speed. Thinks for instance to a
trip from Milan to Turin. By saying that we have made such a trip at an average
speed of 80Km/h, we don’t mean that the whole trip is being covered exactly at
80 km/h at every instant. If we plot the speed versus time during our travel,
the final graph could be similar to the one on page 19 in the textbook:
instantaneous speed varies as time passes, and in general it is a function of
time.
How could we compute instantaneous speed at a given instant in time?
From the mathematical point of view, the idea is to choose a very short time
interval 
close to the instant in which we want to know the instantaneous speed; during
this interval of time we measure the distance covered 
and then we build the ratio 
.
Using Maths, the process could be expressed by the symbols:
The symbol 
means that the ratio is to be
evaluated in the limit of the interval of time
approaching to zero (hence in a very short time of interval). In other words,
instantaneous speed can be thought of as the average speed computed in a smaller
and smaller interval of time.
Notice that, only in the special case of a motion with a constant speed, the
instantaneous speed and the average speed are equal. It is the only case
where it is possible to write 
Average and instantaneous velocity, 
and 
What is the difference between speed and velocity?
Speed is only a scalar. It doesn’t tell us anything about the direction of
motion.
Velocity is a vector, is made by both speed and direction. Speed is the
magnitude of the velocity vector. It is the length of the arrow representing
the velocity.
For instance, diagram 2.5 on page 20 in the textbook shows a car negotiating a
curve with a constant speed. The direction of the velocity changes as the car
moves around the curve, so that the velocity 
is not the same as the velocity 
even though the speed has not changed.
Average velocity is a vector having size equal to the average speed, and having
a direction equal to the one of the displacement vector 
.
Example: A car travels from city A to city B represented by the dots in the
diagram below.
The two cities are 11 Km apart and this distance is covered in 25 minutes. What
is the average velocity in the SI units?
Average velocity is a vector, hence it’s necessary to compute both magnitude
and direction.
Its magnitude is simply equal to the average speed:
Its direction is the same of .
It is represented by the direction of the arrow in the diagram.
Instantaneous velocity can be defined in the same manner as before:
It is a vector having size equal to the instantaneous speed, and having a
direction equal to that of the object motion at that instant.
.