Wavelets

Le wavelets sono particolari tipi di funzioni y(x) che vengono applicate in vari campi di analisi: nella teoria dei segnali, in geofisica, nei processi di denoising, etc. Esse sono usate per scomporre una data f(x), (che può rappresentare un segnale, una superficie, un’immagine, etc.) in funzioni più elementari che racchiudono in loro informazioni riguardanti la funzione f(x) stessa: dalle sue discontinuità al suo andamento generale. Le informazioni che si possono ricavare sono molteplici:

· riducendo un segnale in somma di segnali più semplici si può, ad esempio, risalire alle frequenze di cui è composto;

· si può riconoscere con più facilità l’andamento generale di una superficie f(x,y).

Da un punto di vista matematico, hanno le seguenti caratteristiche:

· y(x) decresce velocemente nel suo dominio ( <¥);

· = 0 valor medio nullo.

Esempi di Wavelet:

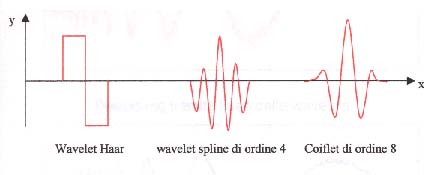
L’analisi wavelets si è sviluppata come una possibile alternativa dell’ analisi di Fourier, in quanto riesce a superarne alcuni limiti. L'analisi di Fourier si compone di due parti: la serie di Fourier e la trasformata di Fourier.

Serie di Fourier:

consente di rappresentare una funzione f(x), periodica di periodo [0,T], in una combinazione lineare di seni e coseni di crescente frequenza.

Trasformata di Fourier:

è l’analogo di quanto visto per la serie, in questo caso, però, cade l’ipotesi della periodicità della f(x), purché questa sia sufficientemente regolare da avere:

Limiti dell’analisi di Fourier:

Nello studio di funzioni attraverso una decomposizione nelle frequenze di cui la funzione è costituita, l’analisi di Fourier non copre tutte le possibilità con cui una funzione può presentarsi e non sempre risponde bene ai diversi tipi di studio che si operano sulle funzioni. I principali aspetti negativi sono:

1.non si adatta molto bene a problemi in cui la funzione oscilli molto poco;

2.un aspetto locale della funzione influenza tutti i coefficienti della trasformata o della serie: ciò significa che se sono presenti errori locali di f(x), essi si distribuiscono su tutta la f(w);

3.usando la trasformata di Fourier la funzione f(x) si può vedere solo nel dominio delle frequenze w. Spesso è invece utile descrivere f(x) sia nelle w che nelle x. Ciò permette, ad esempio, di vedere in quali punti la funzione è composta da determinate frequenze che si vogliono analizzare; oppure di sapere se essa presenta frequenze di fondo comuni a tutti i punti;

4.non si adatta adeguatamente allo studio di problemi non lineari poiché piccole variazioni nell’input possono causare grandi cambiamenti nell’output;

5.per l’analisi di Fourier ogni istante di un segnale è identico ad ogni altro. Infatti, non fornendo informazioni temporali riguardo alle frequenze di ciascun segnale, non rivela quando queste frequenze vengono emesse.

Il problema di rappresentare contemporaneamente la funzione nei due domini si affronta utilizzando un metodo grafico, ossia la “windowed Fourier transform”: si dividono gli assi w e x in segmenti di uguale dimensione. Nel piano (x,w) essi formano una griglia di lati Dw · Dx. Così le “finestre “ di lati generici [ w_j ; w_j+1 ] e [ x_j; x_j+1 ] indicano quali tra le frequenze comprese tra w_je w_j+1 approssimano la funzione nel dominio [ x_j ; x_j+1 ]. Tuttavia, mentre la dimensione della finestra è fissa, il numero di oscillazioni è variabile. Una finestra di dimensioni fisse può essere troppo piccola per le basse frequenze o troppo grande per alte frequenze; non cogliendo così il significato delle stesse (mentre con una grande finestra un’informazione su un piccolo cambiamento verrà perduta nell’informazione che concerne l’intero intervallo corrispondente alla finestra).

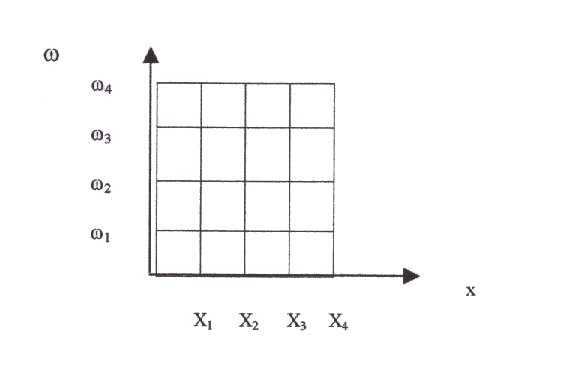
Le wavelets per superare tali limiti:

Rispetto all’analisi di Fourier le wavelets presentano i seguenti vantaggi:

1.risultano essere molto più versatili ai vari tipi di funzione;

2.errori locali nel calcolo della funzione comportano solo errori locali nelle wavelets;

3.la finestra x-w non ha dimensioni fisse ma variabili: all’ aumentare della frequenza essa automaticamente si fa più piccola, catturando quindi i minimi dettagli, mentre s’ingrandisce al diminuire della frequenza.

Grazie alla variabilità della “finestra“ x-w si possono analizzare ed esplorare dettagli di dati che altre metodologie di analisi non permettono di esaminare. Infatti la caratteristica delle funzioni più semplici, ottenute dalla scomposizione della f(x) con l’analisi wavelets, è quella di avere una scala progressivamente minore. Esse cioè recano un livello di dettaglio progressivamente crescente, da una visione d’insieme ad un effetto zoom, in modo da carpire ogni informazione.

Campo di applicazione

L’uso delle wavelets in ambito territoriale deriva dalla possibilità di applicarle a:

·immagini: queste vengono descritte da funzioni bidimensionali f(x,y) a scalino, cioè si tratta di applicazioni discrete che associano ad ogni pixel (i , j) un valore numerico cui corrisponde un colore;

·funzioni bidimensionali f(x,y) interpolanti dati puntuali sul territorio come, ad esempio, densità di popolazione, reddito medio, etc...;

·funzioni ad una sola variabile f(x) da scomporre in modo tale da avere informazioni riguardanti il loro andamento.

Le applicazioni possibili sono quindi le seguenti:

Compressione d’immagini:

trattare un’immagine con le wavelets permette di trasformare i dati dell’immagine, cioè il valore di ogni pixel, in coefficienti wavelets. In entrambi i casi, cioè a partire dai pixel e dalle wavelets, è possibile ricostruire l’immagine originale. Utilizzare l’analisi wavelets è più vantaggioso perché essa consente di utilizzare un basso numero di coefficienti trascurando quelli di valore prossimo a zero. Questo tipo di analisi risulta essere vantaggiosa per immagini uniformi. E’ qui mostrato un esempio di compressione, nel quale si usa un’immagine aerea di Palmanova applicandole un particolare tipo di wavelet e ricostruendo l’immagine usando solamente il 30% dei coefficienti-wavelets.

Esistono algoritmi capaci di immagazzinare solo i coefficienti diversi da zero e, quindi, di ottenere una compressione dell’immagine in termini di spazio fisico all’interno del computer. È da sottolineare, però, che l’annullamento di coefficienti vicini a zero comporta una perdita di informazioni. L’efficienza della compressione consiste, quindi, nello stabilire la soglia di eliminazione in modo da ottenere un’immagine che, ad occhio nudo, sia identica all’originale. Immagine di Messina vista da satellite.

Per la rimozione del disturbo dalle immagini, si scelgono quei coefficienti che sono i maggiori tra coefficienti vicini, corrispondenti (per ogni scala) a punti dell’immagine dove la correlazione tra immagine e wavelet è massima. Questi valori massimi, detti “ wavelet maxima“, corrispondono al disturbo e vengono così scartati.

Trattazione di immagini territoriali:

la caratteristica essenziale dell’analisi wavelets è quella di scomporre una funzione f(x,y) in una serie di funzioni più semplici e di scala crescente. Questa metodologia permette quindi, di poter analizzare l’immagine a risoluzioni variabili: dal dettaglio massimo (immagine originale) all’approssimazione più spinta. Per trasformare l’immagine in una sequenza di coefficienti-wavelets bisogna far si che la matrice contenente i valori di ogni pixel diventi una matrice contenente i coefficienti-wavelets ad ogni risoluzione.

Il grado di risoluzione (gdr) può assumere valori compresi tra 0 e j, dove j è l’esponente da dare a 2 per ottenere la dimensione dell’immagine (2 ^j); cioè se l’immagine è 256 * 256 allora il grado di risoluzione può variare da 0 a 8 (256 = 2 ⁸)

- gdr = 8 approssimazione nulla

- gdr = 0 l’immagine è un punto

Interpolazione di dati:

noti i dati territoriali di qualsiasi genere, è possibile interpolarli con funzioni appropriate e poi trattarli con le wavelets. Il vantaggio che si ottiene consiste nella possibilità di osservare la distribuzione spaziale del fenomeno in esame a vari gradi di risoluzione, in modo da visualizzare il trend di fondo, le discontinuità, etc... Per poter trattare i dati territoriali con l’analisi wavelets bisogna considerare che i valori noti corrispondono a pochi punti (uno per ogni comune) e che quindi è necessario interpolarli in modo da ottenere una funzione polinomiale f(x,y) più uniforme e più facile da trattare. Per una buona interpolazione si possono inoltre sfruttare le immagini territoriali GIS e collocare sui baricentri comunali le informazioni territoriali puntuali.

Esempi di applicazioni dell’interpolazione di dati:

1.Interpolando i dati territoriali riguardanti la popolazione di una provincia si presenta un ovvio problema: il capoluogo di provincia generalmente è molto più popolato dei comuni appartenenti alla provincia stessa. Quindi la superficie f(x,y) presenta un picco molto accentuato centrato sul capoluogo. Quest’ultimo, per essere rappresentato visivamente, fa si che la superficie interpolata venga notevolmente appiattita e ciò non permette di vedere le variazioni che sussistono tra un comune e l’altro. Invece approssimando la f(x,y) grazie alle wavelets si riesce a “smussare“ gradualmente il grosso picco, facendo così emergere le parti della superficie prima non visibili e a “fondere“ i picchi laddove essi sono vicini tra loro. L’effetto globale è quello di mettere in evidenza le aree dove questi picchi minori sono più concentrati.

2.Eliminazione dei dettagli sui confini territoriali di un’area che presenta sui propri confini una serie di irregolarità. L’uso delle wavelets permette di “smussare“ queste discontinuità e di mantenere la forma generale fino ad approssimazioni alquanto spinte.

Analisi di dati territoriali:

tramite l’uso di alcuni tipi di wavelets è possibile ottenere informazioni sull’andamento delle funzioni in esame: trovare in quali punti esse hanno un comportamento lineare, quadratico, cubico o di ordine superiore attraverso l’analisi di coefficienti di dettaglio.

Link e riferimenti

·B. Burke Hubbard: "The world according to wavelets", 1996;

·K Chui: "An introduction to wavelets", 1994;

·E. J. Stollnitz, T. D. DeRose: "Wavelets for computer Graphics: a primer, Part 1", 1994;

·E. J. Stollnitz, T. D. DeRose: "Wavelets for computer Graphics: a primer, Part 2", 1994;

·K Chui: "Wavelets in geophysics", 1994;

·K Chui: "Wavelets: theory, algorithms and application", 1994;

·C. S. Burrus and R. A. Gopinath: "A Tutorial Overview of Wavelets, Filter Banks andInterrelationships";

·T. Edwards: "Discrete Wavelet Transforms: Theory and Application";

·E. Gootman and M. Wickerhauser: "Elementary Wavelets";

·A. Graps: "An Introduction To Wavelets";

·J. Lewalle: "Tutorial on Wavelet Analysis of Experimental Data";

·P. Schroeder and W. Sweldens: "Building Your Own Wavelets at Home";

·B. Vidakovic: "Wavelets for Kids".