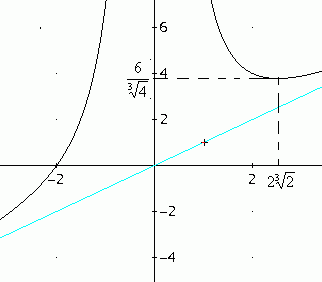Esercizio guida sullo studio di una funzione razionale
Sia data la funzione:
se ne vuole disegnare il grafico dopo averne studiato le proprietà. Per questo scopo si può seguire uno schema come il seguente:
1) Ricerca del dominio
2) Studio del segno
3)Calcolo dei limiti
4)Ricerca degli asintoti
5)Intersezione con gli assi
6)Studio della derivata prima
7)Studio della derivata seconda.
1)Ricerca del dominio
Si osserva che il denominatore deve essere diverso da zero e quindi bisogna
imporre la condizione:
da cui segue:
e perciò il dominio è:
2)Studio del segno
Per studiare il segno si impone la condizione:
e quindi studiando il segno del numeratore e del denominatore si ottiene y(x)>0 per x>-2. Rappresentando graficamente questi dati nel piano xy,escludendo quindi le parti di piano che non possono contenere la curva, si ottiene:
.
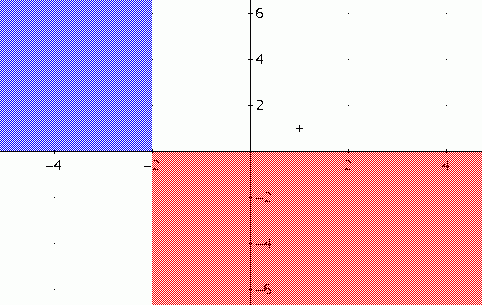3)Calcolo dei limiti
I limiti vanno calcolati nei punti di accumulazione del dominio che in questo
caso sono: -oo, +oo e 0.
Si ha subito:
4)Ricerca degli asintoti
Dal calcolo dei limiti si osserva subito che la retta x=0 è asintoto
verticale e che la funzione non ammette asintoti orizzontali. Quindi è
necessario verificare se esiste qualche asintoto obliquo. Trattandosi di una
funzione razionale senza valori assoluti ci si può limitare al solo studio
in +oo. Perciò si calcolerà il
per sapere se esiste il coefficiente angolare m e in questo
caso si calcolerà l'intercetta q con il
.
Premesso ciò, il primo limite è:
e perciò m=1, quindi ha senso calcolare l'intercetta
q con il secondo limite che in questo caso si specifica in
che, riducendo allo stesso denominatore, diventa:
.
Perciò l'asintoto obliquo ha equazione y=x.
5)Intersezioni con gli assi
Si trovano mettendo a sistema l'equazione della funzione con quella dell'asse
x e con quella dell'asse y, però si deve osservare che la funzione non
possiede intersezioni con l'asse y perchè lo 0 non appartiene al dominio.
Quindi basta risolvere solo il sistema:
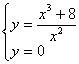che ammette come soluzione il punto:
(-2,0).
6)Studo della derivata prima
Lo studio del segno della derivata prima permette di stabilire la monotonia
della funzione e gli eventuali punti di massimo e di minimo.
Calcolandone l'espressione si ha:
e studiandone il segno si ottiene il grafico:
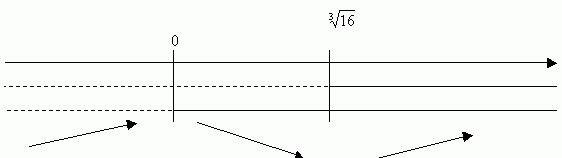
da cui si evince che 
è un
punto di minimo. L'ordinata di questo punto si ottiene calcolando
ottenendo le seguenti coordinate:
.
7)Studio della derivata seconda
Lo studio della derivata seconda permette di individuare la concavità
della funzione e gli eventuali punti di flesso. La sua espressione è:
e si conclude subito che la concavità è rivolta sempre verso l'alto dato che il segno della derivata prima è sempre positivo, ciò comporta anche che non vi sono flessi.
Il grafico della funzione è:
