Dimostrazione relativa alla costruzione geometrica dell'ellisse a partire dai suoi assi
Dettagli della costruzione dell'ellisse
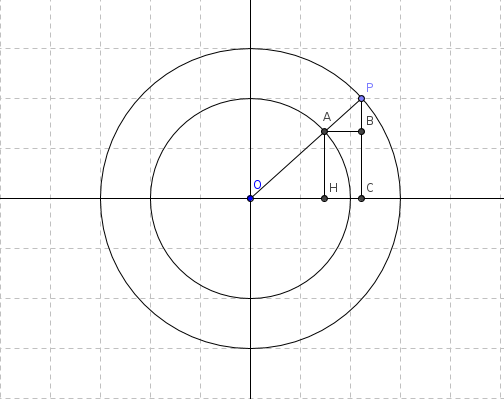
Il punto P appartiene alla circonferenza di raggio a, mentre il punto A appartiene alla circonferenza di raggio b:
xP 2+ yP 2= a2
xA 2+ yA 2= b2
Dobbiamo dimostrare che il punto B appartiene all'ellisse:
xB2/a2 + yB2/b2 = 1
Dalla figura si evince che: xP = xB ed anche yA = yB
L'equazione precedente si puņ riscrivere:
xP2/a2 + yA2/b2 = 1
Questo č da dimostrare. Per fare ciņ partiamo dalla prima circonferenza e dividiamo per a2 :
xP 2/a2+ yP 2/a2= 1
In base alla similitudine dei triangoli OAH e OPC si ha: yP/a = yA/b cioe' yP 2/a2 = yA2/b2 e quindi :
xP2/a2 + yA2/b2 = 1
