6 . Appendice 1
Visualizzazione dell’algoritmo 1:
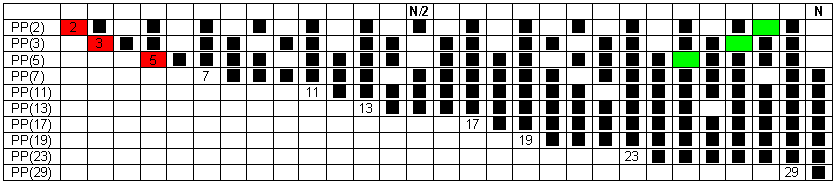
In ciascuna riga della tabella sono indicati mediante quadratini neri
gli elementi di PP(n) a partire da n=2. Le colonne complete
di tali quadratini e appartenenti a n righe consecutive individuano
un elemento dell’insieme PP(2..n). Si cessa di aggiungere
righe – e quindi si sono individuati tutti i numeri primi in (0,N)
– quando fra l’ultimo numero primo individuato e N non compare
più nessuna colonna (inclusiva della riga dell’ultimo numero
primo individuato) completa di tutti i quadratini. Da questa tabella,
in cui si è scelto N=R5=30, è anche
possibile osservare che, rispetto a Rn/2 –
es-sendo Rn il prodotto dei primi n
numeri primi e quindi cadendo in Rn una ricorrenza
di ciascuno dei cicli degli n numeri primi (colonna bianca nelle
righe da 2 a n, con n=5 nell'esempio) –, c’è
perfetta specularità delle ricorrenze PP(i) (i
= 2..n), quindi perfetta specularità degli elementi di
PP(2..n), con l’eccezione descritta dalla proprietà
6.1, secondo la quale da 2 fino a n e da Rn–n
a Rn–2 c’è perfetta contro-specularità
fra numeri primi e cancellazioni.58
Le considerazioni di questa appendice, benché visualizzate, per
ovvie ragioni, solo per Rn=30, sono della massima
generalità, dal momento che la regola di costruzione degli insiemi
PP(n) e la regola dell’individuazione degli elementi degli
insiemi PP(2..n) sono regole invarianti del processo.
È escluso da tutte le considerazioni
il numero 1, definito “numero non primo” all’unanimità.
Si può osservare, al riguardo, l’inevitabile paradosso
secondo cui il primo numero non è un numero primo. |