La geometria come successione di
deduzioni logiche
Analizziamo
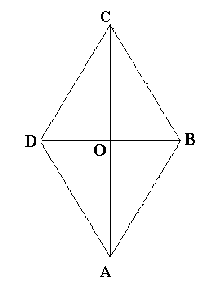
la nota proprietà di un rombo che dice:
"in
un rombo le diagonali sono perpendicolari"
Un
enunciato di questo tipo si chiama teorema.
Oltre
all'enunciato, un teorema comprende l’ipotesi, la tesi, la
dimostrazione.
a)
L’ipotesi è ciò che si suppone di sapere , le proprietà che già si
conoscono;
b)
la tesi è ciò che si vuole dimostrare;
c)
la dimostrazione, è quel processo logico che dall’ipotesi porta alla tesi.
Nel
teorema precedentemente enunciato abbiamo:

Ipotesi: (ABCD è un rombo)
Tesi: AC è perpendicolare a BD
Dimostrazione:
se (ABCD) è un rombo, allora
è un parallelogramma. Ma in un parallelogramma, le diagonali si dividono
scambievolmente a metà (teorema precedente),
quindi DO=OB.
Un rombo ha i lati uguali
(definizione di rombo), allora CD=BC, quindi il triangolo BCD è isoscele.
Nel triangolo BCD, per quanto
detto prima, CO è la mediana (definizione di mediana).
Ma in un triangolo isoscele,
la mediana relativa alla base, coincide con l’altezza (teorema precedente).
Se CO è l’altezza, AC è
perpendicolare a BD. c.v.d.
La dimostrazione di questo teorema utilizza
definizioni e teoremi precedenti.
Anche i teoremi precedenti hanno richiesto una dimostrazione, con l'utilizzo di
teoremi ancora precedenti.
Per non instaurare una catena infinita, bisogna
accettare alcune proprietà degli enti geometrici,
senza darne una dimostrazione formale. Tali proprietà si chiamano assiomi o postulati.
Anche le definizioni che illustrano le figure
geometriche richiedono, per essere formulate, definizioni precedenti;
pertanto bisogna accettare di conoscere alcune figure solo attraverso le loro
proprietà, senza darne una definizione formale.
Queste figure si chiamano enti
fondamentali
o concetti
primitivi.
Concetti
primitivi, assiomi e definizioni fondamentali
Un concetto primitivo è un ente geometrico che si conosce mediante le
sue proprietà senza che se ne dia una definizione formale.
I concetti primitivi fondamentali sono: il punto, la retta, il piano e lo
spazio.
Una definizione è una presentazione di un ente geometrico.
Esempi:
Il segmento è una parte di retta delimitata da due punti;
|
|
A e B si dicono "estremi del segmento" |
Un angolo è una parte di piano delimitata da due semirette aventi la
stessa origine.
|
|
l'origine comune O è detto "vertice" dell'angolo; le semirette a e b sono dette "lati" dell'angolo. |
Sono detti assiomi o postulati, le proprietà di una figura geometrica, che si accettano senza che se ne dia una dimostrazione.
Esempi:
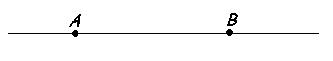 Per
due punti passa una e una sola retta.
Per
due punti passa una e una sola retta.
|
|
Per un punto passano infinite rette. |
|
Quinto postulato di Euclide: data una retta r e dato un punto P, esiste una e una sola retta s
passante per P e parallela ad r . |
|
|
|
Un angolo è una
parte di piano, delimitata da due semirette aventi la stessa origine. Da due semirette si
hanno due angoli: -CONVESSO (parte
viola); -CONCAVO (parte
celeste); Se un testo non
dice niente, si intende l'angolo convesso. |
|
Due angoli si
dicono consecutivi se hanno un lato in comune. Nella figura s è il lato comune ad entrambi gli angoli. |
|
|
|
Due angoli si
dicono adiacenti quando hanno un lato in comune e gli altri due
appartenenti alla stessa retta. Due angoli adiacenti insieme formano un
angolo piatto. |
|
Due angoli si dicono opposti
al vertice quando i lati dell'uno si ottengono prolungando i lati
dell'altro. Teorema :Se due angoli sono
opposti al vertice, allora essi sono uguali. |
|
Per la dimostrazione di questo teorema vedere "Introduzione alla geometria razionale"