INTRODUZIONE
ALLA GEOMETRIA RAZIONALE
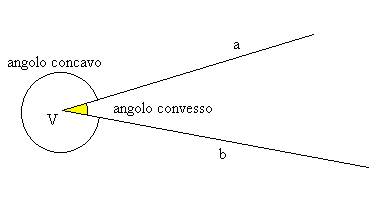
L'origine
comune alle due semirette si chiama vertice dell'angolo (nella figura V
è il vertice).
Le
due semirette a e b si chiamano lati dell'angolo.
L'angolo
più piccolo (quello che non contiene i prolungamenti dei lati) si dice convesso;
quello a destra, più grande (che contiene i prolungamenti dei lati) si dice concavo.
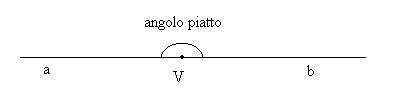
Un
angolo si dice piatto, e si indica con p
, quando i
suoi lati appartengono alla stessa retta.
|
Nella figura a fianco gli angoli a e b
sono opposti al vertice. Dimostrare il seguente teorema: se due angoli sono opposti al vertice, allora essi
sono uguali. Dimostrazione: essendo VC e VD semirette appartenenti alla stessa
retta, si ha
a
+ g = p,
da cui
a = p
- g; essendo VA e VB semirette appartenenti alla stessa
retta, si ha
g
+ b = p,
da cui
b = p
- g; quindi a
= b in quanto si ottengono dalla stessa differenza
( p - g
). |
|
In un teorema ci sono:
l'enunciato (nel
teorema precedente è la frase in corsivo);
l'ipotesi ( Ip ),
cioè quello che già si conosce (nel teorema precedente "a e b
sono opposti al
vertice");
la tesi (
Ts ), cioè quello che bisogna
dimostrare (nel teorema precedente "a
= b ");
la dimostrazione, cioè il ragionamento logico che, partendo dall'ipotesi, arriva alla tesi. ARGOMENTI