Inertial navigation overview

The operation of inertial navigation systems depends upon the Newton’s laws. They tell us  that the external force acting on a body produce a proportional acceleration on it. Given the ability to measure that acceleration, it would be possible to calculate the change in velocity and position by performing successive mathematical integrations of the acceleration with respect to time. Acceleration can be determined using a device known as an accelerometer. An inertial navigation system usually contains three such devices, each of which is capable of detecting acceleration in a single direction. The accelerometers are commonly mounted with their sensitive axis mutually perpendicular. In order to navigate with respect to our inertial reference frame, it is necessary to keep track of the direction in which the acceleration are pointing. Rotational motion of the body with respect to the inertial reference frame may be sensed using gyroscopic sensors and used to determine the orientation of the accelerometers at all times. Given this information, it is possible to resolve the accelerations into the reference frame before the integration process takes place. Hence, inertial navigation in the process whereby the measurements provided by gyroscopes and accelerometers are used  to determine their position of the vehicle in which they are installed. By combining the two sets of measurements, it is possible to define the translational motion of the vehicle within the inertial reference frame and so calculate its position within it. Unlike many other types of navigation system, inertial system are entirely self-contained within the vehicle, in the sense that they are not dependent on the transmission of signals from the vehicle or reception from an external source. However, inertial navigation systems do rely upon the availability of accurate knowledge of vehicle position at the start of navigation. The inertial measurement are then used to obtain estimates of changes in position which take place thereafter.

Inertial navigation process

Therefore the inertial navigation system, INS, is made from a navigation computer and a set of gyroscopes and accelerometers that measure in Newton’s inertial axis. The group of inertial sensors is commonly called inertial measurement unit (IMU). Once aligned to a set of reference axes (such as the North-East-Down set), the sensors provide distance measurements and the navigation computer carries out the continuous dead reckoning calculations. The inertial sensors might be mounted in a set of gimbals so that they stay level and head in a fixed direction no matter how the vehicle moves, so that they are mechanically isolated from the rotational motion of the vehicle. This construction is called a platform system. Alternatively, the instruments might be attached to the vehicle, in which case they measure its motion components in the vehicle axis set, and the system computes direction travelled in the reference axis by transforming the measurements from the vehicle axis to the reference axes. This is called stapdown system, jargon for instrument “strapped down” to the vehicle. This systems have removed most of the mechanical complexity of platform systems, but the major penalties incurred are the substantial increase in computing complexity and the need to use sensors capable of measuring much higher rates of turn. However, advances in computer technology combined with the development of suitable sensors have allowed such design to become realty. Our system is just a strapdown system.

To navigate inertially, we first measure the accelerations in the directions of the navigation axes, and if our instrument are not perfect, we might compensate their reading by removing bias or scale factor errors, perhaps known as a function of the system’s measured temperature. Second, to find the vehicle’s vertical acceleration, we subtract gravity from the “Down” accelerometer output, perhaps using a gravity model to allow for the variation of gravity with latitude and longitude. Third, we integrate the accelerations over a known time, once to get the velocity, twice to get the distance travelled. For periods of constant acceleration we can apply the equation of motion to find the distance travelled, s:

v=v₀+at

s=v₀t+½at²

where a is the acceleration, v is the velocity after time t and v₀ is the initial velocity.

Because integration is the process of summing the outputs at frequent, known interval, we must know the time interval accurately as it enters as a squared term in the distance computation. Fourth, we measure the rotation rates directly with gyroscopes in a strapdown system. We then compensate for gyro bias and possibly scale factor errors, and we determinate a new heading. Fifth, we compensate for earth rotation if we are in local level axes; otherwise the platform would be space stabilized and would seem to tilt in the vehicle axes set. Finally, the combined distance and heading data give us an update dead reckoning position to display. Then we go back to the beginning and do it all over again, until the end of the journey.

Mechanization

The conversion of the navigation equations and their resolution may be done in different possible frame other than the inertial frame. This conversion in known as mechanisation. In this way it is possible to separate the vertical and horizontal channel behaviour making easier the analysis of the platform behaviour and test phase, and mainly isolating the intrinsic instability problem relegating it only to one channel. Just for this intrinsic instability of the vertical channel we decided to insert a pressure sensor in our experiment.

The variations in mechanizations are in the strapdown computational algorithms and not in the arrangement of the sensors or the mechanical layout of the system.

System performance analysis

The accuracy to which a strapdown navigation system is able to operate is limited as a result of errors in the data which are passed to it prior to the commencement of navigation, as well as imperfections in various components which combine to make up the system. The sources of error may be categorised as follow:

• initial alignment errors;

• inertial sensor errors;

• computational errors.

In general, inertial navigation system performance is characterised by a growth in the navigation error from the position co-ordinate values which are initially assigned to it.

For simplicity, now we consider a two-dimensional case and then we assume navigation to take place in the local geographic reference frame. In this system, the x and z reference axes are coincident with the local horizontal and the local vertical respectively, and the navigation system provides estimates of velocity in each of these directions.

The error dynamics of the local geographic system is analysed for the condition where true body attitude is zero, that is, θ=0. In this case, the coupling between  the channels is normally zero, allowing each channel to be analysed separately. In addition, it is assumed that the navigation system in mounted in a vehicle which is at rest to the Earth, or one which is travelling at a constant velocity with respect to the Earth. Under such conditions, the only force acting on the vehicle is the specific force needed to overcome the gravitational attraction of the Earth. In this situation, f_xg=0 and f_zg=g.

The errors equations, corrected to first order, for the vertical and horizontal channels, can now be written as shown in the following table.

Error source		Position error x-axis	z-axis
Initial position errors	δx0	δx0	-
	δz0	-	δz0
Initial velocity errors	δvx0	δv0t	-
	δvz0	-	Δvz0t
Initial attitude errors	δθ0
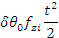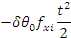Accelerometers biases	δfxb
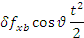	δfzb
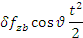Gyroscope biases	δωyb

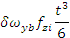Substituting the values of biases provided by the IMU constructor in these equations, the position error would be as high as 20 km after one hour of flight! This result shows that an augmentation system is compulsory when using low cost inertial sensor for navigation purposes. Augmentation is achieved adding sensors that provides auxiliary data, in particular, a pressure sensor used as a barometric altimeter and magnetometers used as auxiliary source for attitude data. Even with these augmentation systems, the position error will grow at unacceptable level, so will be necessary a continuous integration with GPS data. The estimate of the overall position error of our system is one of the main goals of our experiment, so it cannot be estimate a priori.