iso_pari

Si chiama pari (diretta) un'isometria che mantiene il senso di rotazione, si chiama dispari (invertente) un'isometria che inverte il senso di rotazione.


isometria pari: passando da A a B a C si ruota in senso orario come passando da A' a B' a C'	isometria dispari: passando da A a B a C si ruota in senso antiorario mentre passando da A' a B' a C' si ruota in senso orario

Essendo in modo evidente le simmetrie assiali dispari, le isometrie pari sono tutte e solo quelle che si ottengono componendo due simmetrie assiali (vedi teorema 2).
Se gli assi sono paralleli si ha una traslazione, se sono incidenti si ha una rotazione. Potendo due rette essere solo parallele o incidenti le isometrie pari possono essere solo rotazioni o traslazioni.

TEOREMA
Un'isometria è una traslazione se e solo se è il prodotto di due simmetrie assiali con assi paralleli

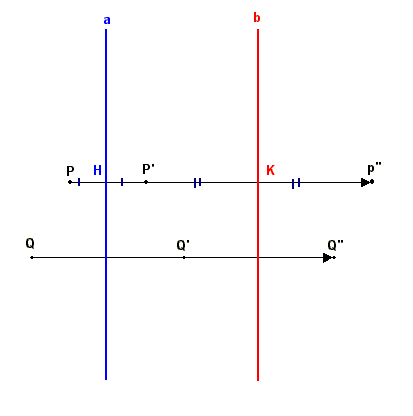Il prodotto di due simmetrie assiali con assi paralleli è una traslazione

La trasformazione a°b è una traslazione che ha:
a) come lunghezza il doppio della distanza tra le rette a e b,
b) come direzione quella perpendicolare a quella delle rette a e b,
c) come verso quello da a verso b.
Al lettore formalizzare la dimostrazione.

Una traslazione individuata da un vettore v si può ottenere come prodotto di due simmetrie assiali con assi paralleli

Preso un qualsiasi segmento orientato rappresentante di v basta assumere come assi di simmetria la perpendicolare al segmento per il suo punto di applicazione e l'asse del segmento. Per la prima parte del teorema si otterrà una traslazione del vettore v.

NOTA 1
E' importante osservare che una traslazione può essere individuata da infinite coppie di assi paralleli, basta che determinino le medesime caratteristiche a, b, c del precedente teorema.

TEOREMA
Un'isometria è una rotazione se e solo se è il prodotto di due simmetrie assiali con assi incidenti

assiincidenti.gif (3001 byte)

Il prodotto di due simmetrie assiali con assi incidenti è una rotazione

La trasformazione r°s è una rotazione che ha:
a) come angolo di rotazione il doppio dell'angolo HOK,
b) come centro il punto di intersezione O tra r ed s,
c) come senso di rotazione quello da r verso s.
Al lettore formalizzare la dimostrazione.

Una rotazione di dato angolo orientato alfa e dato centro O si può ottenere come prodotto di due simmetrie assiali con assi incidenti

Basta assumere come assi la retta del primo lato di alfa e la bisettrice di alfa. Per la prima parte del teorema si otterrà la rotazione di partenza

NOTA 2
E' importante osservare che una rotazione può essere individuata da infinite coppie di assi incidenti, basta che determinino le medesime caratteristiche a, b, c del precedente teorema.