iso_disp

La definizione di isometrie dispari è data assieme a quella di isometrie pari

Le isometrie dispari sono tutte e solo quelle che si ottengono componendo tre simmetrie assiali oppure le simmetrie assiali (vedi teorema 2).

a)    paralleli tra loro
b)    incidenti in uno stesso punto
c)    due paralleli e il terzo perpendicolare (glisso-simmetria)
d)    due parallei e il terzo incidente ma non perpendicolare
e)    incidenti a due a due in tre punti distinti

Dimostreremo che i primi due casi (in blu) si riducono ad una simmetria assiale mentre i casi in verde si riducono al terzo; quest'ultimo individua un tipo di isometria che non abbiamo ancora visto la glisso-simmetria.

Sintetizzando potremo allora dire che le possibili isometrie sono quattro: le simmetrie assiali, le rotazioni, le traslazioni, le glisso-simmetrie (le simmetrie centrali si possono considerare rotazioni di un angolo piatto).

TEOREMA (caso a)
Il prodotto di tre simmetrie assiali con assi parallei è una simmetria assiale

	Alla trasformazione (a°b)°c possimo sostituire (a'°b')°c con b'=c e con a' e b' scelti in modo da individuare la stessa traslazione determinata da a e b: 1 a' e b' devono distare come a e b, 2 a' e b' devono essere paralli ad a e b 3 a' e b' devono essere assegnati con lo stesso ordine di a e b vedi nota del teorema relativo al prodotto di due simmetrie assiali con assi paralleli (n° 1). ma (a'°b')°c=a°(b'°c) perché il prodotto tra applicazioni è associativo, pertanto, poiché b'°c è la trasformazione identica, avremo a'°(b'°c)=a' c.v.d..
TEOREMA (caso b) Il prodotto di tre simmetrie assiali con assi incidenti in uno stesso punto è una simmetria assiale
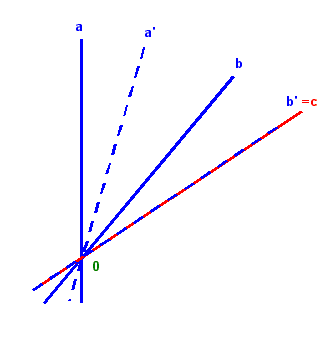
	Alla trasformazione (a°b)°c possimo sostituire (a'°b')°c con b'=c e con a' e b' scelti in modo da individuare la stessa rotazione determinata da a e b: 1 a' e b' devono determinare un angolo congruente a quello determinato da a e b, 2 a' e b' devono intersecarsi nel punto O comune ad a e b 3 a' e b' devono essere assegnati con lo stesso ordine di a e b vedi nota del teorema relativo al prodotto di due simmetrie assiali con assi incidenti (n° 2). ma (a'°b')°c=a°(b'°c) perché il prodotto tra applicazioni è associativo, pertanto, poiché b'°c è la trasformazione identica, avremo a'°(b'°c)=a' c.v.d..
DEFINIZIONE *(caso c)* Il prodotto di tre simmetrie assiali con i primi due assi paralleli e il terzo perpendicolare è una traslazione seguita da una simmetria assiale con asse parallelo al vettore traslazione, una isometria siffatta prende il nome di glisso-simmetria.
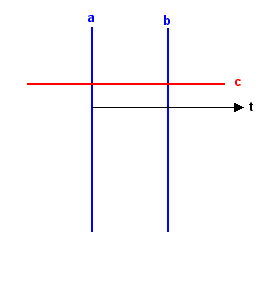	(a°b)°c=t°c

TEOREMA (caso d) Il prodotto di tre simmetrie assiali con i primi due assi paralleli e il terzo incidente, ma non perpendicolare ai primi due, si può ridurre ad una glisso-simmetria

Spostando b e c in modo da mantenere il punto di intersezione e l'angolo tra le due rette (anche in senso di rotazione) si passa dalla situazione A alla situazione B. a°(b°c)=a°(b'°c')

Spostando e b' in modo da disporre a' parallelamente a c' e conseguentemente b" parallelamente a c' si passa dalla situazione B alla situazione D. a°(b'°c')=(a°b')°c'=(a'°b")°c'
	Infine spostando b" e c' in modo da disporre b''' parallelamente ad a' e conseguentemente c" perpendicolarmente a b''' si perviene alla situazione E, cioè ad una glisso-simmetria (a'°b")°c'=a'°(b"°c')=a'°(b'''°c")

TEOREMA (caso e) Il prodotto di tre simmetrie assiali con assi incidenti a due a due si può ridurre al caso del teorema precedente cioè a una glisso-simmetria
	Basta spostare b in b' parallelo ad a e c in c' in modo da mantenere ...