Ottimizzazione della popolazione

Il teorema di Holland stabilisce che i building blocks possono incrementare esponenzialmente il numero di loro individui generazione dopo generazione, la questione diventa allora: perchè questa potrebbe essere una buona strategia?

La domanda ci porta a un ben analizzato problema di decisione statistica, quello della slot machines a due braccia. L'esempio potrebbe sembrare fuorviante, tuttavia si capirà come la strategia applicata dagli algoritmi genetici coincida con quella che permette di vincere al gioco [1] .

Supponiamo di avere a disposizione una slot machines a due braccia, con due fessure per le monete, una per ogni braccio. Il giocatore inserisce la moneta in una delle due fessure, tira il relativo braccio e incassa la vincita oppure inizia un nuovo gioco. Assumendo che il guadagno per giocata medio sia $\mu_1$ con varianza $\sigma_1^2$ per il primo braccio braccio e sia $\mu_2$ con varianza $\sigma_2^2$ per il secondo braccio, ponendo per semplicità $\mu_1 > \mu_2$.

Il giocatore ignaro potrebbe chiedersi su quale lato possa essere più vantaggioso giocare, avendo a dispozizione $N$ monete, e quale sia la strategia per massimizzare la vincita. Non disponendo di informazioni riguardo le vincite programmate, ci si trova di fronte a un duplice compito: dover decidere dove giocare la prossima moneta per vincere e dover trarre informazione su quele sia il lato vantaggioso, disponendo di un numero finito di monete.

Si tratta quindi di dover bilanciare due strategie contrastanti, una che si riassume nel concetto di esplorazione, l'altra nel concetto di sfruttamento. Pertanto in questo gioco, come negli algoritmi genetici, per raggiungere l'obiettivo che ci si è prefissi, è necessario un compromesso tra l'esplorazione delle potenzialità delle soluzioni candidate e il loro sfruttamento.

Chiaramente disponendo di un numero finito di generazioni e separando le due fasi, si rischia che prolungando troppo la fase di esplorazione, non ne rimangano abbastanza per sfruttare appieno l'informazione acquisita, dualmente invece disponendo di poca informazione l'algoritmo potrebbe essere troppo lento nell'evolvere verso soluzioni ottime, o addirittura convergere verso soluzioni banali.

Tornando all'esempio della slot machines, disponendo di $N$ monete, se ne allochiamo $n$ per braccio per la fase di esplorazione, con $2n<N$ , in modo che si possono utilizzare le rimanenti $N-2n$ per monetizzare le informazioni raccolte.

Assumendo che $q(n)$ sia la probabilità che dopo la fase di esplorazione si ritenga favorevole il braccio che in realtà non lo è, le perdite possono essere quantificate in

$$L(N,n)=(\mu_1-\mu_2) \cdot ((N-n)q(n)+n(1-q(n)))$$

dove con $(\mu_1-\mu_2) \cdot ((N-n)$ si indica la perdita netta. Nel caso invece si decida esattamente su quale sia il braccio migliore, cosa che accade con probabilità $1-q(n)$, la perdita è ridotta a quello che si è speso per fare il test su quel braccio e cioè $(\mu_1-\mu_2) \cdot n$.

Utilizzando il teorema del limite centrale, possiamo approssimare l'andamento di $q(n)$ con la coda della distribuzione gaussiana normalizzata:

$$q(n)\approx \frac{1}{\sqrt{2 \pi}} \cdot \frac{e^{-\frac{c^2}{2}}}{c} \; \; \; c=\frac{\mu_1-\mu_2}{\sigma_1 ^2-\sigma_2 ^2} \cdot \sqrt{n}$$

è evidente che il valore da assegnare a $n$ non dovrà essere nè troppo piccolo, nè prossimo a $\frac{N}{2}$, si impone quindi una strategia di compromesso.

Holland studiando in dettaglio questo problema arrivò alla conclusione che la strategia ottima è descritta dalla seguenta equazione:

$$n^*\approx b^2 \ln \left( \frac{N^2}{8 \pi b^4 \ln N^2} \right) \; \; \; b=\frac{\sigma_1}{\mu_1-\mu_2} \; ,$$

che porta a scrivere:

$$N-n* \approx \sqrt{8 \pi b^4 \ln N^2} \cdot e^\frac{n^*}{2b^2} .$$

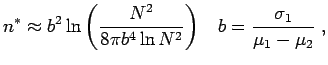
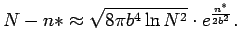
Pertanto la strategia ottima prevede di assegnare al braccio che sembra più favorevole un numero di monete poco maggiore di $e^\frac{n^*}{2b^2}$.

Il problema della slot machine e l'algoritmo genetico sono quindi simili; infatti dati due schemi di ordine uno, che hanno il loro unico bit assegnato nella medesima posizione, per il teorema di Holland, l'algoritmo decide implicitamente per uno dei due schemi, in base alla media del fitness degli individui che appartengono ai due schemi, in questo senso l'algoritmo risolve in parallelo molti problemi della slot machine.

Generalizzando a schemi di ordine superiore, dati due schemi concorrenti con un numero arbitrario di bit uguali in determinate posizioni, l'algoritmo sceglie per uno dei due valutando un numero enorme di problemi della slot machine a n-braccia in parallelo.