In questo paragrafo si riporta l'enunciato e la dimostrazione del teorema dello schema, enunciato da Holland nel 1975. Si può ritenere sia il risultato fondamentale nella teoria sugli algoritmi genetici, anche se non può ritenersi confrontabile con i risultati presentati per i problemi di ottimizzazione deterministica, tuttavia chiarisce i principi di funzionamento impliciti degli algoritmi genetici.
Riferendoci al generico algoritmo genetico dotato di funzione di fitness ![]() si introducono le seguenti notazioni:
si introducono le seguenti notazioni:
| (5.1.4) |
 |
(5.1.5) |
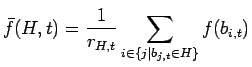 |
(5.1.6) |
Dimostrazione
La probabilità di selezionare un individuo che appartiene allo schema ![]() è
è
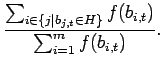 |
(5.1.8) |
Questa probabilità non cambia all'interno del ciclo di selezione, infatti ognuno degli ![]() individui può venire selezionato indipendentemente dagli altri. Quindi il numero di individui selezionati che appartengono a un certo schema
individui può venire selezionato indipendentemente dagli altri. Quindi il numero di individui selezionati che appartengono a un certo schema ![]() è una distribuzione binomiale su
è una distribuzione binomiale su ![]() campioni.
campioni.
Si ottiene pertanto che il numero atteso di individui che appartengono ad ![]() è
è
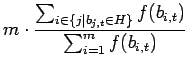 |
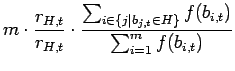 |
(5.1.9) | |
 |
(5.1.10) |
Se due individui appartenenti ad ![]() vengono incrociati, i loro figli apparterranno ancora ad
vengono incrociati, i loro figli apparterranno ancora ad ![]() . L'unico modo per far diminuire il numero di individui di
. L'unico modo per far diminuire il numero di individui di ![]() è quello di incrociare un'individuo che non appartiene ad
è quello di incrociare un'individuo che non appartiene ad ![]() con uno che vi appartiene, con cesura della stringhe scelta arbitrariamente tra i bit assegnati di
con uno che vi appartiene, con cesura della stringhe scelta arbitrariamente tra i bit assegnati di ![]() .
.
La probabilità che il punto di incrocio sia scelto all'interno della lunghezza di definizione di ![]() è
è

Quindi la probabilità di sopravvivenza dello schema ![]() , cioè la probabilità che una stringa che appartiene ad
, cioè la probabilità che una stringa che appartiene ad ![]() , produca figli ancora appartenti ad
, produca figli ancora appartenti ad ![]() può essere stimata nel modo seguente, dove con
può essere stimata nel modo seguente, dove con
![]() si indica la probabilità di cross over:
si indica la probabilità di cross over:
 |
(5.1.11) |
Sfruttando la relazione precedente si può scrivere pertanto il numero atteso di stringhe che appartengono allo schema ![]() dopo l'operazione di cross over nella forma
dopo l'operazione di cross over nella forma
Dopo l'operazione di cross over tuttavia interviene l'operatore di mutazione che può alterare l'individuo nei bit assegnati di ![]() , e far si che non possa più appartenere allo schema.
, e far si che non possa più appartenere allo schema.
La probabilità che tutte gli individui che appartengono ad ![]() rimangano inalterati dopo una operazione di mutazione è
rimangano inalterati dopo una operazione di mutazione è
| (5.1.13) |
Il teorema di Holland viene sviluppato rispetto alla semplice operazione di cross over uniforme, tuttavia può essere analogamente esteso a implementazioni che utilizzano altri operatori di mutazione e cross over.
![$\displaystyle E[r_{H,t+1}] \geqslant r_{H,t} \cdot \dfrac{\bar f(H,t)}{\bar f(t)} \cdot P_\mathbf{C} (H) \cdot P_\mathbf{M} (H)$](img428.png) |
(5.1.14) |
Il teorema di Holland, a una prima interpretazione appare sicuramente poco esplicativo, apre inoltre numerose questioni che sembrano rendere ancora più nebulosa la questione della convergenza verso le soluzioni ottime.
Dapprima è necessario notare che in base alla 5.1.7, gli schemi con fitness superiore alla media e distanza minima tendono a produrre più figli che gli altri. Gli schemi con questa proprietà vengono chiamati building blocks. Se assumiamo che il rapporto

Questo ci impone di capire se sia una strategia saggia quella di far crescere esponenzialmente il numero di soggetti appartenenti a uno schema con fitness superiore alla media e distanza breve.
Tenuto conto che l'algoritmo genetico lavora su stringhe e non su schemi, il teorema di Holland fornisce informazioni in parallelo su come tutti gli schemi possano crescere in popolazione se il loro fitness è superiore alla media, ridursi altrimenti.
Nei prossimi paragrafi si affronteranno queste due questioni; prima l'ottimizzazione della popolazione e poi il parallelismo implicito degli algoritmi genetici.