Elementi di statistica

Come già accennato, la PMD è per sua natura un fenomeno di tipo aleatorio. Utilizzando il modello a lamine, cioè modellando una fibra lunga a birifrangenza aleatoriamente variabile come una successione di spezzoni di fibra a birifrangenza costante, accoppiati in modo casuale, si può ritenere che le sezioni siano statisticamente indipendenti ed abbiano uguali proprietà statistiche.

Si indichi con $n$ il numero di lamine o spezzoni con cui si discretizza la fibra e sia $\mathbf{\Omega}_{n}$ il vettore di dispersione di polarizzazione sulla $n$-esima sezione.

É ragionevole pensare, ed è dimostrabile in termini rigorosi, che per una fibra lunga, per la quale cioè $n\rightarrow\infty$, le componenti di $\mathbf{\Omega}$ sono variabili aleatorie gaussiane statisticamente indipendenti a media nulla e varianza $\sigma^{2}$. Ne consegue che il DGD, pari al modulo di $\mathbf{\Omega}$, è una variabile aleatoria maxwelliana [5] [3] e quindi la sua densità di probabilità risulta

$$f_{\vert\mathbf{\Omega}\vert}(x)=\frac{32x^{2}}{\pi^{2}\tau^{3}}e^{-\frac{(\frac{2x}{\tau})^{2}}{\pi}}$$ (2.10.1)

dove con $\tau$ si indica l'apettazione della variabile $x$, $E[x]$.

Dalla 2.10.1 si può calcolare agilmente il momento del secondo ordine $E[x^{2}]$ che vale

$$E[x^{2}]=\frac{3 \pi \tau^{2}}{8}.$$ (2.10.2)

Anche per il secondo ordine di PMD è nota la distribuzione statistica; più esattamente, si può dimostrare che vale la seguente relazione [10]

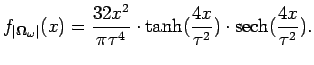$$f_{\vert\mathbf{\Omega}_{\omega}\vert} (x)= \frac {32x^{2}}{\pi \... ...\mathrm{tanh} (\frac{4x}{\tau^{2}}) \cdot \mathrm{sech} (\frac{4x}{\tau^{2}}) .$$ (2.10.3)

Operando la scomposizione dell'espressione vettoriale $\mathbf{\Omega}_{\omega}$ nelle sue componenti parallela $\mathbf{\Omega}_{\omega \vert\vert}$ e perpendicolare $\mathbf{\Omega}_{\omega \perp}$

$$\mathbf{\Omega}_{\omega}=\mathbf{\Omega}_{\omega \vert\vert}+\mat... ...ga \perp}= \Delta \tau_{\omega} \cdot \hat q +\Delta \tau \cdot \hat q_{\omega}$$ (2.10.4)

è possibile ricavare la distribuzione statistica del termine di dispersione cromatica [9], nella forma

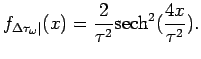$$f_{\Delta \tau_{\omega}\vert}(x)=\frac{2}{\tau^{2}} \mathrm{sech^{2}}(\frac{4x}{\tau^{2}}) .$$ (2.10.5)

Dalla teoria statistica sono inoltre note le relazioni che legano le potenze medie del primo e secondo ordine di PMD, [10] [9]

$$E[\Delta \tau_{\omega}^{2}] = \frac{1}{27} E^{2}[\Delta \tau^{2}]$$ (2.10.6)

$$E^{2}[\Delta \tau^{2}] = 3 E[\vert\Omega_{\omega}\vert^{2}] .$$ (2.10.7)