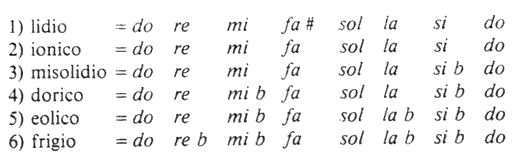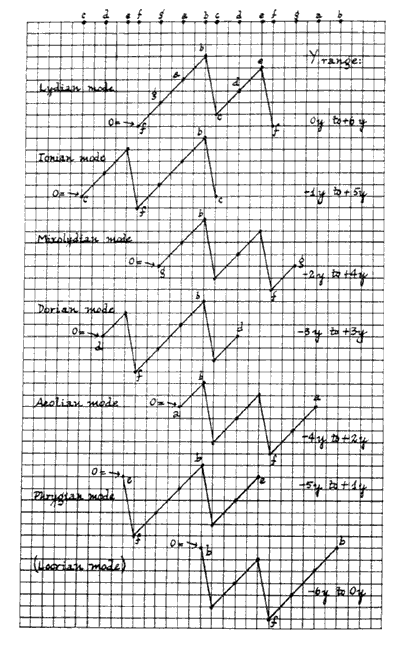
Immaginiamo di considerare le note di ogni scala modale come punti di un piano secondo questo criterio:

• sull’asse delle x abbiamo il numero di semitoni di cui la nota dista dalla finalis
• sull’asse delle y abbiamo il numero di quinte di cui la nota dista dalla finalis.

Rappresentando così le scale modali vediamo subito che alcuni modi hanno un aspetto simile:

Pensiamo di ordiniamo le scale secondo questo criterio di similitudine.

Partendo dal modo lidio finiremo col modo frigio.

Trasportiamo ora le scale in modo tale che tutte partano dalla stessa nota (per esempio do).

Notiamo che una scala ha in comune con la successiva il maggior numero di note possibili.

Pensiamo ora a ogni scala come a un quadrato nel piano.

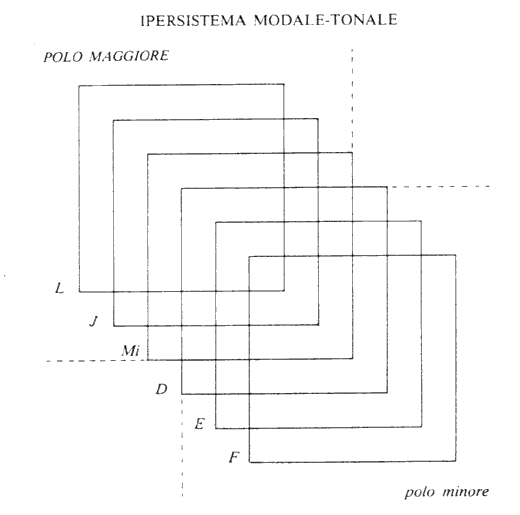
L’intersezione di due piani rappresenta le note in comune.

Notiamo subito che ci sono delle note comuni a tutte le scale: il primo e il quinto (ossia il primo e il quinto grado delle scale).

Consideriamo questi suoni come fissi, come vera ossatura immutabile del nostro sistema.

Se consideriamo invece le intersezioni tra aree contigue, vediamo che queste sono hanno l’area massima possibile.

Un solo suono ha la possibilità di muoversi tra due stati diversi.

Questo avviene per i suoni 2, 3, 4, 6, 7 (e quindi per i relativi gradi della scala).

Questi gradi risultano dunque mobili, in quanto in relazione alla finalis possono presentarsi secondo intervalli sia maggiori sia minori.

Se denominiamo il polo lidio “maggiore” e quello opposto “minore”, vediamo che abbiamo costruito un sistema centrale imperniato sulla finalis e sulla quinta e oscillante tra due poli opposti.

Possiamo rappresentare schematicamente questo fenomeno in questo modo:

Questo sistema permette di giustificare le opposizioni di triadi maggiori e minori così tipiche delle Toccate frescobaldiane: non si tratta di opposizione di modi, ma di continue oscillazioni di un unico ipermodo.