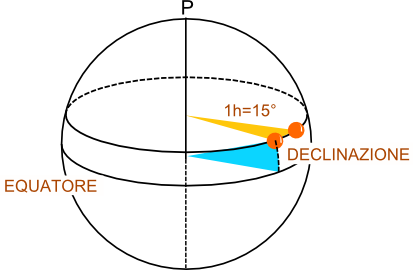
Movimento apparente del Sole nel cielo. Nell'arco delle 24 ore compie una rotazione completa attorno all'asse polare.
Gianpietro Favaro 2010-1.0
La costruzione di meridiane può essere affrontata oggi con una gran quantità di ausili informatici. Primo fra tutti il bellissimo programma di Gian Casalegno “Orologi Solari” disponibile in rete all'indirizzo digilander.libero.it/orologi.solari. Anche in letteratura abbondano i testi su questo argomento e la Sezione UAI dedicata alle meridiane (quadrantisolari.uai.it) fornisce una importantissima sorgente di informazioni.
Tuttavia, nel mio percorso di studio delle meridiane mi sono trovato di fronte a schemi di costruzione prefabbricati o formule complete e precisissime che non soddisfacevano la mia curiosità. A costo di reinventare l'acqua calda, ho messo a punto un metodo geometrico che mi ha permesso di mettere a fuoco le problematiche di realizzazione e di affrontare con maggior sicurezza il progetto degli orologi solari.
Per questo scopo si è fatto uso dei seguenti strumenti informatici:
OpenOffice Calc
OpenOffice Writer
QCad
Qt Designer
Inkscape
Per la sorgente degli algoritmi si è utilizzato, tra gli altri, l'insostituibile volume “Astronomical Algorithms” di Jean Meeus ed il bellissimo documento redatto da Henning Umland “A short guide to Celestial Navigation”, disponibile in rete.
Nella costruzione di meridiane si assume che il Sole, nel suo moto apparente attorno alla Terra, compia una rivoluzione di 360° attorno all'asse polare in 24 ore. Pertanto il Sole si sposterà nel cielo dell'osservatore di 15° ogni ora in un piano perpendicolare all'asse polare.
|
|
Movimento apparente del Sole nel cielo. Nell'arco delle 24 ore compie una rotazione completa attorno all'asse polare. |
Pertanto uno stilo parallelo all'asse polare proietterà un'ombra sul piano equatoriale che compierà un giro completo nelle 24 ore e quindi suddividerà il cerchio in 24 settori omogenei da 15° ogni ora. La costruzione di questa meridiana piana risulta estremamente semplice.
|
|
L'ombra proiettata dallo stilo verticale (gnomone) replica l'andamento del Sole e pertanto disegna un cerchio e ne percorre la circonferenza alla velocità di 15° l'ora |
Le cose si complicano quando il piano di proiezione non è il piano equatoriale ma essenzialmente si tratta di calcolare opportune proiezioni di questa meridiana piana.
|
|
Schema di meridiana polare piana |
Questo metodo si propone inizialmente di realizzare meridiane piane orizzontali o verticali per proiezione diretta della meridiana piana polare.
I parametri necessari per disegnare la meridiana polare sono la latitudine e la longitudine del luogo nel quale la meridiana va posizionata.
La latitudine fornisce il grado di distorsione della proiezione piana, la longitudine, invece, fornisce l'informazione sulla collocazione dei marcatori del tempo medio sul piano della proiezione dell'ombra dello gnomone.
|
|
Proiezione della meridiana polare sul piano orizzontale dell'osservatore alla latitudine lat |
Il tempo medio, indicato dall'orologio, si riferisce al centro del settore di 15° che definisce il fuso orario di riferimento. Ad esempio, il nostro fuso orario, un'ora in anticipo rispetto all'ora di Greenwich, si riferisce alla longitudine di 15°E. Tuttavia la longitudine, ad esempio, di Venezia, è di 12.5°E, 2.5° prima del centro del fuso orario. Il risultato è che, se vogliamo che la meridiana indichi l'ora media, la meridiana polare deve essere corretta (ruotata) della differenza di tempo corrispondente alla distanza angolare tra la longitudine del luogo ed il centro del fuso orario.
|
|
La meridiana polare deve essere ruotata di un angolo corrispondente alla differenza angolare tra il centro del fuso orario e la longitudine del luogo. Ad esempio, alla longitudine di Venezia (12.5°E) la meridiana polare deve essere ruotata di 2.5° (b) in senso antiorario (il mezzogiorno dell'orologio viene raggiunto in anticipo rispetto all'ora vera indicata dalla meridiana). Infatti l'ora media del fuso orario di Venezia è quella del meridiano 15°E. |
|
|
Il tempo indicato dall'orologio è un tempo convenzionale che non tiene conto delle variazioni del tempo solare indotte dalle differenti velocità del moto apparente del Sole vero (equazione del tempo) |
Esperimento: è il 15 aprile ed hai appena comperato un bellissimo e precisissimo orologio. Decidi di usarlo per determinare la durata del giorno. Aspetti il passaggio del Sole al meridiano (mezzogiorno) e fai partire l'orologio. Attendi il giorno dopo ed il successivo passaggio al meridiano. Annoti la durata registrata dall'orologio e ne fai la base per la misura dei giorni. Metti in moto il meccanismo e ti affidi all'orologio per determinare l'istante del mezzogiorno perché i giorni seguenti il Sole è sempre oscurato dalle nuvole. Finalmente un mese dopo, il 14 maggio, le condizioni sono propizie e riesci a misurare l'istante del passaggio del Sole al meridiano. Con tua grande sorpresa e disappunto, scopri che tra l'istante del mezzogiorno indicato dall'orologio ed il passaggio al meridiano del Sole c'è una differenza di più di 3 minuti e mezzo!! Eppure l'orologio che hai comperato doveva avere una precisione straordinaria! Non può essere. Forse hai sbagliato qualcosa e ripeti le operazioni di sincronizzazione. Lasci andare avanti il meccanismo e, stavolta, controlli periodicamente il passaggio del Sole al meridiano. INCREDIBILE! Ti accorgi che con il passare dei mesi l'istante del passaggio del Sole al meridiano non è costante ma anticipa e ritarda rispetto al tuo orologio superpreciso. Ma cosa succede? Forse la velocità di rotazione della Terra non è costante ed è influenzata da qualche energia misteriosa? L'entità di questa oscillazione è molto ampia e raggiunge anche 16 minuti e mezzo di differenza con il tuo orologio! Come si può spiegare il fenomeno senza disturbare la rotazione della Terra?
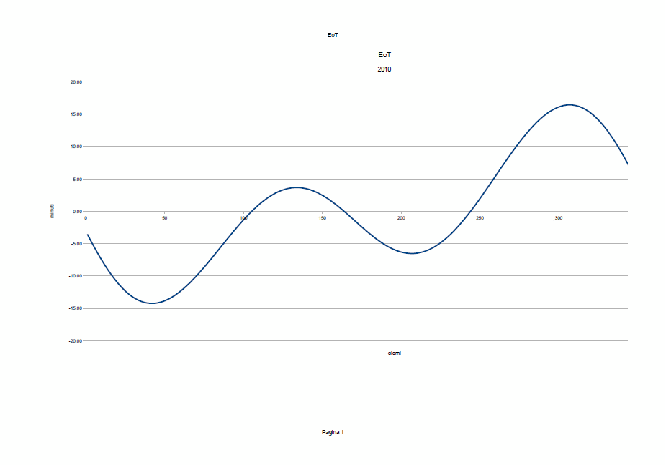
Andamento
dell'Equazione del Tempo durante l'anno (differenza tra il tempo
dell'orologio – tempo medio, ed il tempo della meridiana –
tempo vero)
L'andamento si presenta apparentemente complesso.
E' dovuto a due cause indipendenti: l'eccentricità dell'orbita terrestre attorno al Sole e l'inclinazione dell'asse terrestre sull'eclittica (piano di rivoluzione della Terra attorno al Sole).

Effetto dell'eccentricità dell'orbita sulla durata del giorno: nel disegno, l'eccentricità e la velocità di rivoluzione sono fortemente accentuate.
All'istante A viene fatto partire l'orologio di riferimento. Si attende il successivo passaggio del Sole al meridiano che avviene in B. Nel frattempo, però la Terra si è spostata per il moto di rivoluzione e quindi l'angolo che deve essere sotteso per riportare il Sole in meridiano è >360°, ad esempio, 400°. Per avere, perciò, due passaggi del Sole in meridiano al perielio occorrerà che la Terra compia, quindi, una rotazione di 400°.
Decidiamo che questo intervallo temporale, misurato dall'orologio, fissa la durata del giorno (24ore).
All'afelio, poiché la Terra tra C e D si muove più lentamente, l'angolo che la Terra dovrà percorrere per avere due passaggi successivi del Sole al meridiano risulterà inferiore a 400°, ad esempio 370°. Di conseguenza il Sole sarà già transitato al meridiano quando l'orologio segnerà lo scadere delle 24 ore (400°). La durata del giorno non sarà perciò costante durante l'anno.
Questo fenomeno è ciclico ed ha il periodo di 1 anno.
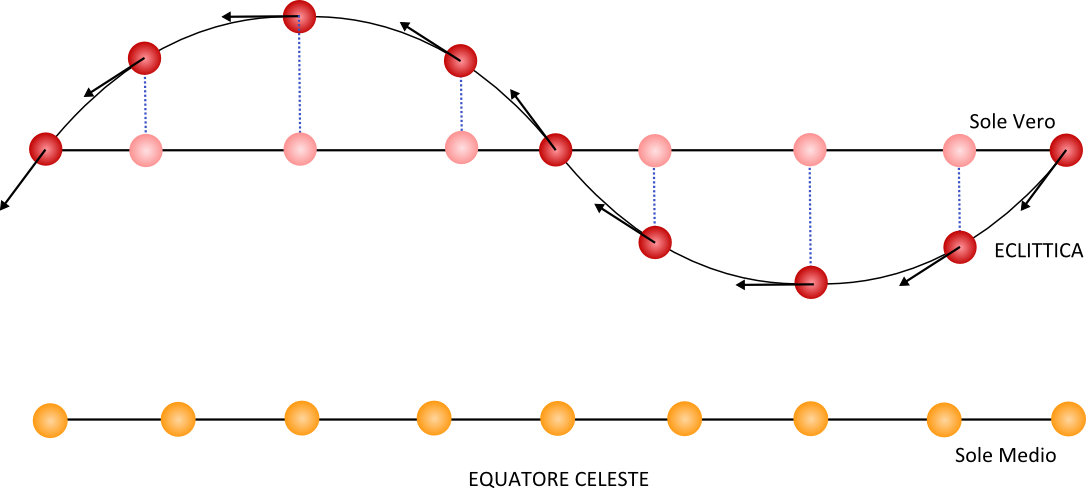
Se l'orbita della Terra attorno al Sole fosse un cerchio perfetto, la durata del giorno non sarebbe comunque costante. Infatti l'inclinazione dell'asse terrestre sull'eclittica ha l'effetto di desincronizzare il tempo medio con il tempo vero. Il moto apparente del Sole avviene lungo la linea dell'eclittica che risulta inclinata di circa 23.5° sul piano dell'equatore celeste.
Per 6 mesi si trova sopra l'equatore celeste e per 6 mesi si trova al di sotto di quest'ultimo. L'eclittica incrocia l'equatore celeste in due punti, all'equinozio di primavera (da sotto a sopra) e all'equinozio di autunno (da sopra a sotto). Il tempo medio si riferisce ad un sole fittizio che si muove NON sull'eclittica ma sull'equatore a velocità costante. I due soli, quello vero e quello medio, coincidono agli equinozi e ai solstizi.
Il sole vero si muove sull'eclittica a velocità costante (se eccettuiamo l'effetto dell'eccentricità dell'orbita terrestre) ma il sole medio (tempo dell'orologio) si muove con velocità costante sull'equatore. I “due soli” non sono allineati e il sole medio a volte si trova in anticipo, a volte in ritardo, rispetto al sole vero (tempo della meridiana).
Questo fenomento è ciclico ed ha il periodo di 6 mesi.
La composizione dei due fenomeni dà origine alla curva dell'equazione del tempo.
|
|
|
Keith C. Heidorn
Per questa operazione farò uso di un CAD grafico che facilita le manipolazioni geometriche degli elementi che compongono la meridiana.
|
|
Suddivisione uniforme in 24 settori (meridiana polare). Il Sole nel suo movimento apparente proietta l'ombra dello stilo verticale alla velocità costante (eccezion fatta per l'EOT) di 15°/ora. |
|
|
Rotazione, oraria o antioraria, per tener conto dello scostamento della longitudine del luogo dal centro del fuso orario di riferimento del tempo medio (-2.5° alla longitudine di Venezia, antiorario) |
|
|
Ellisse ottenuta per proiezione del cerchio della meridiana polare alla longitudine del luogo (45°). Lo schiacciamento sarà tanto più pronunciato quanto minore sarà la latitudine. Asse minore B = sen(lat). |
|
|
L'ellisse ottenuta è in realtà la meridiana orizzontale, alla latitudine lat, vista di scorcio. Da questa vista le proiezioni delle ore rispecchiano quelle della meridiana polare, ma occorre riportare la suddivisione delle ore sul cerchio distorto dalla prospettiva corrispondente all'ellisse. Per farlo, da ogni intersezione dei raggi orari della meridiana polare con l'ellisse, si traccia una linea verticale che va ad intersecare il cerchio esterno (linee verdi). |
|
|
L'intersezione di queste linee con il cerchio mostra la posizione delle ore nella meridiana orizzontale alla latitudine lat (linee azzurre). |
Per ottenere una meridiana verticale, orientata a sud, occorre disegnare l'ellisse utilizzando per l'asse minore il coseno della latitudine anziché il seno. Nella figura che segue viene presentato il caso per la latitudine 30°N.
|
|
Alla latitudine di 30°N la meridiana orizzontale è vista dal polo con un asse minore pari a OH (sen(lat)) mentre la meridiana verticale è vista con l'asse minore pari a OV (cos(lat)). |
|
|
|
|
Applicazioni |
|
|
|
|