Michele Emmer

"Mathland. Dal mondo piatto alle ipersuperfici"

(La rivoluzione Informatica)
Italia, 2003Testo&Immagine (Universale di Architettura, n. 143)

La matematica ha cambiato profondamente l'idea che abbiamo oggi di spazio, facendoci capire che in un certo senso siamo noi a creare e inventare lo spazio attraverso il mutare delle nostre idee su di esso.
Michele Emmer descrive questo cambiamento di idee attraverso un viaggio dove si è guidati dal Quadrato e dalla Sfera del libro di Edwin A. Abbott "Flatlandia : racconto fantastico a più dimensioni" .
Il viaggio si fonda su sei pilastri necessari per capire il nuovo mondo dove ci porteranno le due figure geometriche :
1_lo spazio euclideo : spazio della perfezione, dello spazio platonico, fondato su definizioni e assiomi.
2_la libertà : la matematica è il regno della libertà dove si inventano oggetti nuovi, nuove teorie e nuovi problemi.
3_come queste idee vengono trasmesse : ossia come vengono comprese dai diversi settori della società
4_il computer : idea geniale di un matematico, strumento sofisticato, insostituibile.
5_il progresso : i nuovi risultati non cancellano i precedenti.
6_le parole : parole simboliche, metaforiche che fanno ormai parte del linguaggio comune.

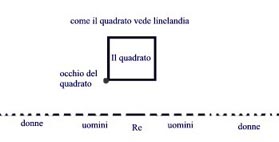
Il Quadrato abita il mondo a due dimensioni, Flatland, appunto, mentre la Sfera quello a tre dimensioni.
Per gli abitanti di Flatland non si può nemmeno immaginare l'esistenza di un mondo a tre dimensioni perchè il loro mondo è fatto come di ombre dai contorni luminosi che si spostano sulla superficie di un foglio di carta.
Per cui la solo cosa che gli abitanti di Flatland vedono della Sfera che è scesa dal mondo a tre dimensioni a fargli visita, è una linea che rappresenta la sezione tra il piano dove vivono gli abitanti di Flatland e la Sfera.

La Sfera spiega al Quadrato l'esistenza di un mondo a tre dimensioni, il Quadrato dapprima inorridito da questa idea si compiace poi della scoperta di un nuovo mondo e inferforato da questa novità ipotizza l'esistenza di un altro mondo a quattro dimensioni applicando lo stesso ragionamento che la Sfera gli aveva spiegato poco prima .
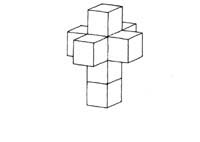
Compare così il cubo a quattro dimensioni, l'ipercubo, generato dalla traslazione di un cubo lungo un quarto asse perpendicolare allo spazio tridimensionale, l'ipercubo ha 16 vertici, 32 spigoli, 24 facce.

In campo artistico i primi a intuire che la geometria dello spazio non era più solo quella euclidea e che ci fosse una quarta dimensione furono i Cubisti, ma il movimento che la comprese più a fondo fu il Futurismo dove la quarta dimensione non era più statica e astratta come la intesendevano i cubisti, ma teneva conto della forma che viene creata dal succedersi degli stati di moto.
Alcuni artisti hanno rappresentato l'ipercubo tra cui Theo Van Doesburg nel progetto per una casa privata e Salvador Dalì nel dipinto Crucifixion, ma la vera svolta si ha con il computer grazie al quale si realizza il desiderio del Quadrato di vedere una Sfera e un Cubo a quattro dimensioni.

Marcos Novak, ha reinterpretato questi concetti derivanti dalla matematica rinforzando il ponte architettura e matematica :

"Lo spazio, come sappiamo, è a un tempo non euclideo, curvo e multidimensionale, e contiene più di tre dimensioni spaziali.[...]Spazio e superfici sono quindi interconnesse : entrambi sono multipli, la differenza tra iperspazio e ipersuperficie consiste nel fatto che un'ipersuperficie di un iperspazio a n dimensioni è un sottomultiplo di n-1 dimensioni.
Quindi l'ipersuperficie di un iperspazio a quattro dimensioni spaziali è uno spazio a tre dimensioni spaziali, prodotto tramite una proiezione, una sezione o uno screening."

Emmer chiarisce, infine, il concetto di topologia usando una definizione di Poincaré :

"la topologia è la scienza che ci fa conoscere le proprietà qualitattive delle figure geometriche non solo nello spazio ordinario, ma anche nello spazio a più di tre dimensioni"

Nel 1958 il matematico August Ferdinand Mobius inventa una nuova superficie dello spazio tridimensionale, il nastro di Mobius appunto.

Questa superficie ha interessanti proprietà : la si può percorrere tutta lungo l'asse più lungo tornando al punto di partenza e senza aver mai attraversato alcun bordo; il nastro ha una sola faccia, non c'è esterno e non c'è interno.
Interessante è l'esperienza di Max Bill, architetto e artista, che scrisse un articolo dal titolo "Come cominciai a fare superfici a faccia unica", dove descrive la sua scoperta del nastro di Mobius pensando di aver inventato una forma nuova.
Egli realizzò delle sculture utilizzando questa forma tra cui "Endless Ribbon" presentato per la prima volta alla Triennale di Milano del 1936.

Tra gli architetti contemporanei perticolarmente interessati ha queste forma sono Ben Van Berkel e Carolin Bos (UN STUDIO) che hanno usato il nastro di Mobius come diagramma della loro Mobius house e la bottiglia di Klein, una superficie chiusa ad una faccia senza esterno ne interno, per la stazione di Arnhem.

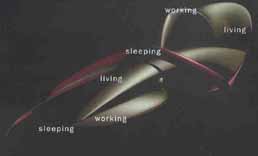
La Mobius house è organizzata come un percorso continuo che si rigira e si piega su se stesso; l'edificio è organizzato in relazione alle attività di chi vi abita, le traiettorie si incontrano in alcuni punti secondo un diagramma ad anello, vi è una conpentrazione continua tra interno ed esterno.

Emmer citando Stephen Perrella afferma :

"la topologia architettonica è la mutazione della forma, della struttura, del contesto e del programma in modelli compositi e dinamiche complesse"

In conclusione Michele Emmer ci ricorda che le parole più importanti per un architetto sono fantasia e libertà, parole che hanno permesso all'architettura contemporanea di arricchire il suo patrimonio progettuale.
Una bella lezione per chi credeva, prima di leggere questo libro, che la matematica fosse l'esatto contrario!