L'algoritmo di approssimazione

Campionamento della curva

La curva che si vuole approssimare con una curva di Bézier, può essere fornita al programma sotto forma di immagine in vari formati (BMP, PNG). Ci sono però alcune semplificazioni che ho introdotto per non complicare l'algoritmo che trasforma la curva fornita in punti elaborabili dall'algoritmo di approssimazione:

1. La curva deve essere un'immagine nera o grigio-scura a 256 tonalità di grigio su fondo bianco;
2. La curva deve cominciare a sinistra e finire a destra: deve cioè avere almeno una colonna a sinistra in cui c'è un solo pixel nero (punto di inizio) e una colonna a destra con la stessa proprietà (punto di fine);
3. La curva non può incrociare se stessa;
4. Lo spessore della curva deve essere abbastanza piccolo (max 2-3 pixel).

La curva quindi deve essere abbastanza ``buona''.

L'algoritmo di campionamento è molto semplice. Partendo da una certa posizione iniziale cerca di ``camminare'' sulla curva, guardando sempre i pixel adiacenti e scegliendo il ``più nero''.

Ovviamente ci sono dei controlli per fare in modo che l'algoritmo vada ``sempre avanti'' e non percorra più volte lo stesso tratto di curva: quando si controllano i pixel adiacenti, vengono esclusi quelli che non sono lungo la direzione di movimento della precedente scelta; quando ciò non è possibile, si cambia direzione, escludendo sempre quella contraria alla direzione attuale (se questa fosse l'unica scelta possibile, vuol dire che si è arrivati alla fine della curva).

Riporto qui il codice:

const int max_points=300; // max numero di punti di campionamento
static int passo=25;      // in pixel
const int soglia_MAX=100;

punto *camp; // vettore di punti di campionamento

int campiona(QImage *q){
  int soglia=soglia_MAX;
  punto destro;
  camp=new punto[max_points];

  // Cerca il pixel nero piu' a sx
  for(int c=0;c<q->width();++c){
    bool row=false;
    for (int r=0;r<q->height();++r)
      if ( qGray(q->pixel(c,r))<soglia){
        soglia=qGray(q->pixel(c,r));
        camp[0].x=c;
        camp[0].y=r;
        row=true;
      }
    if (row) break; // rompe il for sulle colonne
  }
  // Cerca il pixel nero piu' a dx
  for(int c=q->width()-1;c>=0;--c){
    bool row=false;
    for (int r=q->height()-1;r>=0;--r)
      if ( qGray(q->pixel(c,r))<soglia){
        soglia=qGray(q->pixel(c,r));
        destro.x=c;
        destro.y=r;
        row=true;
      }
    if (row) break; // rompe il for sulle colonne
  }
  /* Adesso cammino sulla curva: guardo gli 8 pixel intorno
     al mio e scelgo il piu' nero. Questo mi dira' la direzione
     da seguire (ascisse crescenti o decrescenti.) Quando ad
     un certo punto le ascisse cercheranno di decrescere, avro'
     finito di percorrere una catena. */
  int x_cur=int(camp[0].x);
  int y_cur=int(camp[0].y);
  int x_old1=0, y_old1=0;
  int tmp_gray,i;
  int direzione=0;
  int cambi=0; // cambi di direzione
  //  3 0
  //   X        <-- direzioni
  //  2 1
  //
  bool a_destra, in_alto;
  for (i=passo;i<max_points*passo;++i){
    a_destra = (direzione==0 || direzione==1);
    in_alto  = (direzione==0 || direzione==3);
    soglia=soglia_MAX;
    if ( a_destra)
      for (int j=0;j<3;++j){  // colonna dx
        if ((tmp_gray=qGray(q->pixel(x_cur+1,y_cur-1+j)))
                                       <soglia){
          soglia=tmp_gray;
          camp[i/passo].x=x_cur+1;
          camp[i/passo].y=y_cur-1+j;
        }
      }  //for j
    if (!a_destra)
    for (int j=0;j<3;++j){  // colonna sx
      if ((tmp_gray=qGray(q->pixel(x_cur-1,y_cur-1+j)))
                                        <soglia){
        soglia=tmp_gray;
        camp[i/passo].x=x_cur-1;
        camp[i/passo].y=y_cur-1+j;
      }
    }  //for j
    
    if ((tmp_gray=qGray(q->pixel(x_cur,y_cur-1)))
                                <soglia)  // in alto
      if ( (y_cur-1!=y_old1) && (in_alto) ){ 
        soglia=tmp_gray;
        camp[i/passo].x=x_cur;
        camp[i/passo].y=y_cur-1;
      }
    
    if ((tmp_gray=qGray(q->pixel(x_cur,y_cur+1)))
                               <soglia)  // in basso
      if ( (y_cur+1!=y_old1) && (!in_alto) ){ 
        soglia=tmp_gray;
        camp[i/passo].x=x_cur;
        camp[i/passo].y=y_cur+1;
      }

    if (soglia==soglia_MAX){
      if(++cambi==1)
        if (direzione==1)
          direzione=0;
        else 
          direzione=(direzione+1)%4;
      if (cambi==2)
        if (direzione==0)
          direzione=2;
        else
          direzione=(direzione+2)%4; //no -1 altrimenti...!  
      if (cambi>2){
        return i/passo+1;
      }
      --i; // ripeti il ciclo
      continue;
    }
    cambi=0;
    x_old1=x_cur;
    y_old1=y_cur;
    x_cur=int(camp[i/passo].x);
    y_cur=int(camp[i/passo].y);    
    if ((x_cur==destro.x)&&(y_cur==destro.y)){
      return i/passo+1;  // raggiunta la fine della curva
    }
  }
  return i/passo+1;
}

Approssimazione della curva campionata

L'idea alla base dell'algoritmo che approssima la curva campionata parte da una proprietà delle curve di Bézier: quando i punti di controllo tendono a $\infty$ la curva coincide con i punti di controllo stessi. Questo in pratica vuol dire che la curva segue molto fedelmente i suoi punti di controllo se questi sono ``abastanza numerosi''. Dunque i punti che provengono dal campionamento sono una buona prima approssimazione della curva data in ingresso.

A questo punto ho elaborato un algoritmo che sposta i punti in modo da modificare la relativa curva di Bézier in modo che si avvicini sempre di più ai punti che provengono dal campionamento. L'algoritmo è Greedy, cioè cerca sempre il punto di controllo che effettua lo spostamento maggiore e lo sposta.

Dopo aver scelto il punto da spostare, ho pensato che la direzione migliore di spostamento, quella che modifica di più la curva, è quella perpendicolare alla curva stessa, perpendicolare calcolata in un punto della curva prossimo al punto di controllo che deve essere spostato.

Per calcolare la perpendicolare in un punto di una curva di Bézier, è sufficiente trovare la derivata in un punto della curva(che mi dà la direzione della tangente): sfruttando la forma polinomiale di Bernstein e posto $\Delta b_j=b_{j+1}-b_j$ si ha:

$$\frac{d}{dt}b^n(t)=n\sum_{j=0}^{n-1}\Delta b_jB_j^{n-1}(t)$$

Questa formula è facilmente realizzabile:

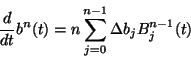
inline punto Bern_der(punto contr[],int punti,double t){ 
  punto tmp;
  tmp.x=0;
  tmp.y=0;
    for(int j=0;j<=punti-1;++j){
      double coef=BernPoly(j,punti-2,t);        
      punto del=delta(contr,1,j);
      tmp.x+=(del.x)*coef;
      tmp.y+=(del.y)*coef;
    }
    tmp.x*=punti-1;
    tmp.y*=punti-1;
  return tmp;
}

mentre la funzione delta(...) usa una formula più generica per restituire il $\Delta^rb_i=\sum_{j=0}^r {r\choose j}(-1)^{r-j}b_{i+j}$.

inline punto delta (punto contr[],int r, int i){
  punto ret;
  ret.x=0;
  ret.y=0;
  for (int j=0;j<=r;j++){
    ret.x+=binom[r][j]*pow_i(-1.0,r-j)*contr[i+j].x;
    ret.y+=binom[r][j]*pow_i(-1.0,r-j)*contr[i+j].y;
  }
  return ret;
}

A questo punto non resta che descrivere come l'algoritmo cerca il punto da spostare:

$\triangleright$

viene eseguito un ciclo su un certo numero di punti della curva di Bézier (saltando ad intervalli di 10 punti) e per ogni punto considerato viene ``tracciata'' una perpendicolare che è lunga circa 20 pixel sullo schermo;

$\triangleright$

la perpendicolare viene intersecata con i segmenti che costituiscono la spezzata che si ottiene unendo i punti che provengono dal campionamento;

$\triangleright$

se vi è intersezione tra i due segmenti, (espressi in forma parametrica con una combinazione convessa dei vertici) viene preso il parametro (quello che descrive il segmento) della perpendicolare e confrontato con i precedenti;

$\triangleright$

alla fine del ciclo si sceglie il massimo tra i parametri descrittori del segmento e dopo averlo scalato per il solito fattore di zoom, viene usato come quantità di spostamento del punto di controllo che corrispondeva al segmento che intersecava la perpendicolare.

L'algoritmo tiene traccia anche di eventuali riduzioni del numero di punti effettuate: è quindi possibile rieseguire l'algoritmo di approssimazione dopo aver effettuato una o più riduzioni (che portano ad un allontanamento della curva di Bézier da quella originaria). Ovviamente meno punti di controllo si hanno, meno precisa potrà essere l'approssimazione.

void paper::guess(){
  for (int volte=0;volte<20;volte++){
    double l1,l2,maxl1=0,maxl,maxm;
    int maxj,j;
    
    disegna_curva(curva,*t_val,curva->size());
    for (unsigned int i=10;i<points;i+=10){
      // Trovo la perpendicolare alla curva
      punto x0y0=Bern(cp,ncp,t_val->at(i));
      punto tmp2=Bern_der(cp,ncp,t_val->at(i));
      double m=-tmp2.x/tmp2.y; // m_perp=-1/m_tg
      // Trova i due punti di controllo che
      // intersecano la perpendicolare
      // do' una certa lunghezza alla perp (~20 px)
      double l=20.0/(xscale*m);  
      if (abs(m)<1){ 
        // cout <<"m piccolo!"<<endl; 
        l=30.0/xscale;
      }
      l1=0;j=1; // il primo e l'ultimo punto NON SI MUOVONO
      while (l1==0&&j<num_camp-2){
        for (int h=0;h<2;++h){
          double p[8];
          //test intersezione
          p[0]=x0y0.x;
          p[1]=x0y0.y;   //A0
          
          p[2]=x0y0.x+l;
          p[3]= m*(l)+x0y0.y; //A1     
          
          p[4]=campioni[j].x/xscale; //B0
          p[5]=campioni[j].y/yscale;
          
          p[6]=campioni[j+1].x/xscale;  //B1
          p[7]=campioni[j+1].y/yscale;
          if (interseca(p,l1,l2)) break;
          else {l=-l;l1=0;} //prova dalla parte opposta...
        }
        ++j;
      }
      if (maxl1<l1){
        maxl1=l1;
        maxj=j;
        maxm=m;
        maxl=l;
      }
    }
    int y=maxj,x=maxj;
    // trovo il corrispondente punto "ridotto"
    for (int h=0;h<riduzioni;++h){ 
      y=(x/4)*3; //blocco di appartenenza
      if ((x%4==1)||(x%4==2)) ++y;
      if (x%4==3) y+=2;
      x=y;
    }
    QString t("Moving"+QString::number(y)+"("+QString::number(maxj)+
              ") with l1= "+ QString::number(maxl));
    emit(message(t));
    moveControlPoint(y,int((cp[y].x+maxl)*xscale+.5),
                     int((cp[y].y+maxm*maxl)*yscale+.5) ); 
  }
}

Non riporto qui il codice relativo alla gestione dell'interfaccia grafica, che per altro non interessa per lo studio vero e proprio delle curve di Bézier.

Nelle prossime pagine riporto le figure citate nel testo e altre che mostrano alcune caratteristiche del programma: intersezione e divisione di una curva).

Infine riporto alcuni esempi di prova dell'algoritmo di approssimazione.

Alcuni commenti finali: le curve di prova le ho disegnate con il mouse, quindi sono un po' irregolari. Le caratteristiche di continuità delle curve di Bézier alcune volte impediscono una corretta approssimazione, soprattutto nei casi in cui c'è una brusca variazione di direzione nella curva (discontinuità nelle derivate).