Metodi di tracciamento della curva

Algoritmo di de Casteljau

L'algoritmo di de Casteljau permette di costruire la curva di Bézier associata al vettore di punti di controllo assegnato procedendo mediante successive combinazioni convesse dei punti stessi:

detti: $b_0, b_1, \ldots, b_n$ i punti di controllo

posto: b_i⁰ = b_i

si ha:

$$b_i^r = (1-t)b_i^{r-1}(t) + tb_{i+1}^{r-1}(t)\quad \left\{ \b... ...ots,n\\ i=0,\ldots,n-r\end{array}\right., \quad t \in\mathbb{R}$$

Il punto della curva di Bézier corrispondente al parametro t assegnato è b₀ⁿ(t).

In particolare, dato che si vuole ottenere una curva di Bézier compresa tra il primo punto di controllo e l'ultimo, si farà in modo che $0\leq t \leq 1$.

Scrivendo infine i coefficienti intermedi b_i^r(t) secondo lo schema di de Casteljau:

$$\begin{array}{cccccc} b_0 \\ b_1 & b_0^1 \\ b_2 & b_1^1 ... ...n & b_{n-1}^1& \ldots &\ldots &b_1^{n-1} &b_0^n \\ \end{array}$$

si nota che durante l'elaborazione è possibile usare un vettore colonna per memorizzare i punti mano a mano che vengono calcolati: ogni elemento, per essere calcolato, ha bisogno solo del valore corrente e del valore dell'elemento successivo.

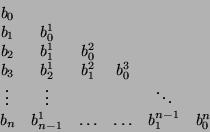
Riporto qui il codice che calcola un punto della curva di Bézier con il metodo sopra esposto; è costituito dalla funzione Castel(...), che accetta come parametri di input rispettivamente il vettore dei punti di controllo (contr[]), il numero di punti di controllo (punti) ed il valore del parametro t (sta_t); gli altri parametri servono per i sotto-punti di controllo e li spiegherò più avanti.

inline punto Castel (punto contr[], int punti, double sta_t,
                     double end_t=0, int whatcp=0) {
  double t=sta_t;
  // copia i punti di controllo
  punto *tmp_cont=new punto[punti];
  for (int i=0;i<punti;++i)
    tmp_cont[i]=contr[i];
  
  if (end_t==0){ // Restitisce un un punto della curva
    for (int c=punti-1;c>0;--c){
      for (int i=0;i<c;++i){
        tmp_cont[i].x=(1-t)*(tmp_cont[i].x)+ t* (tmp_cont[i+1].x);
        tmp_cont[i].y=(1-t)*(tmp_cont[i].y)+ t* (tmp_cont[i+1].y);
      }
    }
  }
  else{ //Restituisce un punto di controllo della curva "ridotta"
    for (int c=punti-1;c>0;--c){
      for (int r=0;r<c;++r){
        if (whatcp>r) // see the blossom notation
          t=end_t;
        else
          t=sta_t;
        tmp_cont[r].x=((1-t)*(tmp_cont[r].x)+ 
                       (t)*(tmp_cont[r+1].x)); 
        tmp_cont[r].y=((1-t)*(tmp_cont[r].y)+
                       (t)*(tmp_cont[r+1].y));
      }
    }    
  }
  punto tmp=tmp_cont[0];
  delete tmp_cont;
  return tmp;
}

Il tipo di output (punto) è una semplice struttura che serve per memorizzare punti di $\mathbb{R}^2$ in coordinate cartesiane:

struct punto {
  double x;
  double y;

  punto(double _x=0,double _y=0){
    x=_x;
    y=_y;
  }
};

La complessità di questo algoritmo è O(n²) per ogni punto della curva, dato che effettuo due cicli innestati sul vettore dei punti di controllo che viene passato in ingresso.

Forma polinomiale di Bernstein

Un altro modo per tracciare le curve di Bézier si ottiene usando i polinomi di Bernstein. Questi sono polinomi del tipo:

$$B_i^n(t)= {n\choose i} t^i(1-t)^{n-i}.$$

Infatti un punto della curva di Bézier corrispondente ad un certo valore del parametro t si può calcolare considerando una proprietà di questo tipo di polinomi:

$$b^n(t)=b_0^n(t)= \sum_{j=0}^n b_jB_j^n(t).$$

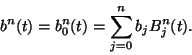
Computazionalmente questo metodo, essendo O(n), è più rapido rispetto a quello di de Casteljau, ma richiede alcuni calcoli ``pesanti'' come ad esempio il calcolo del coefficiente binomiale. Io ho aggirato questo problema tabulando proprio quest'ultimo: quando il programma viene lanciato, costruisce una tabella di coefficienti binomiali, così il calcolo non viene ripetuto ogni volta che si vuole disegnare la curva.

La parte di codice relativa a questo metodo si divide in due parti: la funzione BernPoly(...) che restituisce il valore del polinomio di Bernstein di grado n di ordine i calcolato in t e la funzione Bern(...) che come la funzione Castel(...) riportata sopra restituisce il punto della curva corrispondente al vettore di controllo contr[] con un numero di punti pari a punti, con un valore del parametro t. Le due funzioni si basano sulle formule sopra riportate.

inline double BernPoly(int i, int n,double t){
  return binom[n][i]*(pow_i(t,i)) * pow_i((1-t),(n-i));
}

inline punto Bern(punto contr[],int punti,double t){ 
  punto tmp;
  tmp.x=0;
  tmp.y=0;
    for(int j=0;j<punti;++j){
      double coef=BernPoly(j,punti-1,t);        
      tmp.x+=contr[j].x*coef;
      tmp.y+=contr[j].y*coef;
    }
  return tmp;
}