4 - I tredici solidi di Archimede

Questi solidi sono detti "semiregolari" perché composti da due o tre tipi di facce. I più semplici si ottengono troncando opportunamente i vertici dei cinque solidi platonici, altri invece si ottengono partendo da uno già troncato e ripetendo nuovamente la troncatura dei vertici. Quelli più complessi si ottengono ripetendo più volte la troncatura.

Il primo dei solidi di Archimede si ottiene asportando con un taglio netto i vertici del tetraedro, si ottengono così quattro nuove facce triangolari e si trasformano le facce triangolari preesistenti in quattro esagoni. Per ottenere questo effetto i tagli devono distare dai vertici di un terzo della lunghezza dei lati, se invece la troncatura coincide con la metà dei lati si ottiene ancora un tetraedro. Si incomincia col suddividere i lati in tre parti e poi si congiungono i punti relativi con delle rette che saranno il riferimento per i tagli come mostra la seguente figura:

Il secondo solido di Archimede si ottiene troncando sia il cubo che l’ottaedro, in questo caso il taglio deve coincidere con la metà dei lati come mostra la seguente figura:

Il terzo solido semiregolare è quello che, leggermente modificato, si presta meglio di ogni altro per sperimentare energie legate alla forma come vedremo nel prossimo capitolo. Si ottiene troncando sia il dodecaedro che l’icosaedro col taglio che coincide con la metà del lato:

Il quarto e il quinto solido semiregolare si ottengono rispettivamente dall’ottaedro e dal cubo col taglio che dista dal vertice di un terzo della lunghezza del lato:

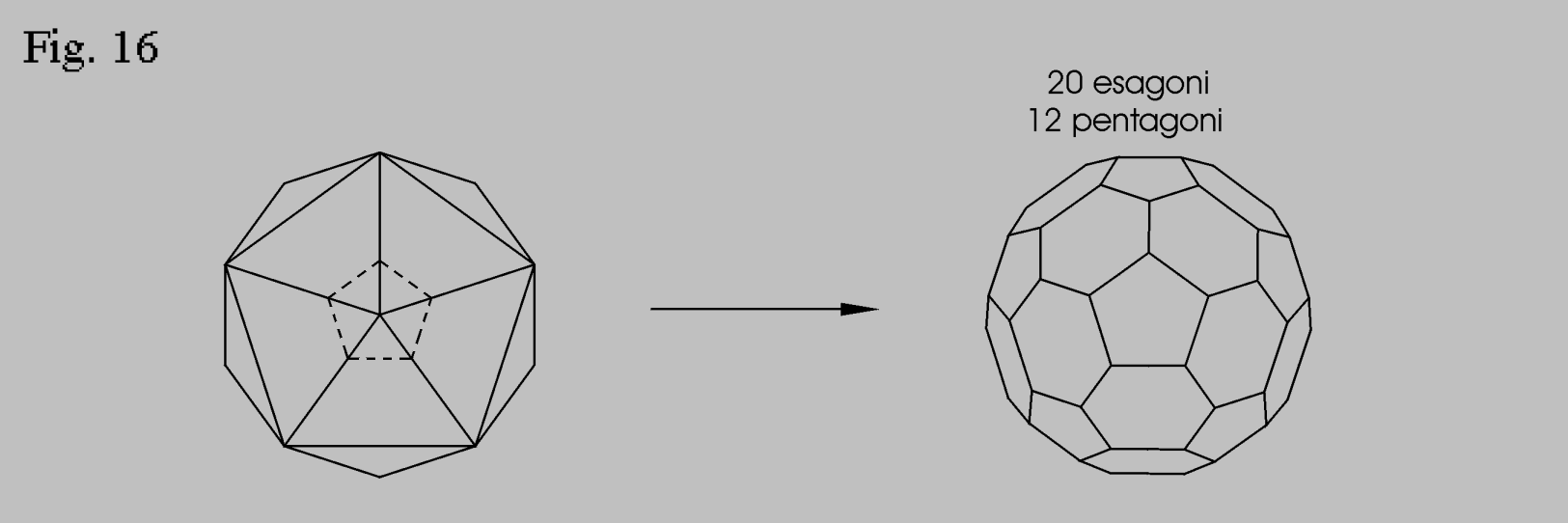
Il sesto solido semiregolare si ottiene dall'icosaedro col taglio che dista dal vertice di un terzo della lunghezza del lato come mostra la seguente figura (le cuciture del pallone usato nel gioco del calcio riproducono questo sesto solido):

Gli altri sette solidi della serie sono rappresentati nella seguente figura senza commenti: