
SCARICA IL PACCHETTO:
formato normale (schermi da 1280x1024 in su) - 93,3 kB
formato ridotto (schermi 1024x768) - 88,6 kB: in questa versione la schermata del programma è stata resa più compatta per trovar posto in uno schermo di formato più comune, per quanto un po' a discapito della chiarezza. Le funzionalità delle due versioni sono le stesse.
Il programma è stato riscritto i molte parti, correggendo alcuni errori e migliorando il funzionamento.
Ringrazio gli appassionati che, cimentandosi con varia fortuna nell'uso del
programma, hanno contribuito e contribuiscono alla sua crescita segnalando sviste,
imperfezioni e idee per miglioramenti.
0 - SOMMARIO:
2 -ESEMPIO D'USO DEL PROGRAMMA ADOPERANDO LA MODELLAZIONE AUTOMATICA
3 -ESEMPIO D'USO DEL PROGRAMMA IMPORTANDO UN DISEGNO PRODOTTO ESTERNAMENTE
4 - FUNZIONAMENTO DEL PROGRAMMA
4.1 - Elenco degli script componenti il pacchetto
4.2 - Modellazione automatica dello scafo
4.3 - Calcolo del volume proprio e del baricentro dello scafo
4.4 - Valutazione della stabilità statica
5 - FORMATI DI ESPORTAZIONE
5.1 - Formato stl
5.2 - Formato fbd
Calcnav permette di modellare automaticamente uno scafo o importare uno scafo già disegnato
ed eseguire calcoli di stabilità.
Il programma è stato ideato inizialmente per tracciare rapidamente il disegno di scafi tondi definendone le
caratteristiche geometriche sulla base di un numero limitato di parametri (lunghezze e angoli fondamentali),
ricavarne il disegno in diversi formati ed eseguire la verifica di stabilità statica dello scafo con eventuali
carichi aggiuntivi.
Il modellatore automatico del programma consente di tracciare solo scafi tondi con specchio di poppa piatto;
è possibile però importare disegni di scafi o generici galleggianti diversi ottenuti con
programmi di disegno assistito, eventualmente modificando o integrando il disegno prodotto da calcnav, ed
eseguire il calcolo di stabilità su di essi, ricavandone numerose informazioni accessorie importanti per il progetto
(baricentro dello scafo, baricentro della parte immersa, pescaggio a diversi angoli, momenti d'inerzia dello
scafo vuoto e carico). È inoltre possibile ricavare la modellazione solida dello scafo.
Naturalmente la speranza è di migliorare ulteriormente il programma e le sue possibilità di
impiego, ricavandone uno strumento di utilità per appassionati e studiosi.
Il programma mette a disposizione dell'utente un'interfaccia grafica che consente una comoda impostazione dei parametri e provvede alla modellazione dello scafo usando opportune famiglie di curve di interpolazione, ed infine all'esecuzione dei calcoli di stabilità.
Per il disegno si è scelto di avvalersi di un altro programma, cioè Blender, potente e raffinato programma di rendering tridimensionale, liberamente scaricabile e facilmente interfacciabile con dati in ingresso. Calcnav stesso esporta la forma dello scafo in formati interpretabili da altri programmi, mentre attraverso Blender è possibile esportare verso ulteriori, numerosi tipi di formati, in modo da poter facilmente acquisire il disegno dello scafo con qualunque programma di disegno assistito.
L'importazione di disegni esterni avviene sempre attraverso il formato stl.
I risultati del calcolo vengono rilasciati sotto forma di documento di testo, apribile con qualunque elaboratore di testo e attraverso il grafico del diagramma di stabilità.
Calcnav è scritto in python, un efficiente linguaggio di programmazione che non prevede la creazione di file "eseguibili", ovvero dei programmi che di solito vengono rilasciati pronti per essere eseguiti da un sistema operativo; non per questo il suo uso risulta complicato! Semplicemente, perché il programma funzioni è necessario che sul calcolatore sia installato l'interprete python,
che, se non già disponibile (è molto diffuso) si scarica liberamente da internet, come viene spiegato poco appresso.
In questo modo, fra l'altro, l'utilizzatore può facilmente sincerarsi che il codice non abbia
scopi maligni (non contenga cioè virus o simili), dal momento che può tranquillamente scorrerlo (ci vuole un po' di pazienza)
e verificarne ogni riga, a differenza di un "eseguibile" chiuso.
Il programma è stato scritto e testato in ambiente GNU/Linux, ma
funziona anche con altri sistemi operativi, grazie alla versatilità
del python e di Blender: seguendo con un po' di pazienza le
istruzioni non avrete difficoltà a farlo funzionare con
soddisfazione sul vostro computer.
1) Scaricate il pacchetto “Calcnav” e decomprimetelo.
Otterrete una cartella di nome "calcnav" che contiene diversi documenti; il programma
da lanciare è “calcnav-x.y.z.py” (al posto di
x,y,e z troverete dei numeri, tanto più alti quanto più
avanzata è la versione rilasciata del programma).
Sistemi windows: cliccate su “calcnav-x.y.z.py”.
Sistemi Unix/Linux: aprite una shell nella cartella e lanciate il programma
nel modo consueto:
$./calcnav-x.y.z.py
eventualmente, se il programma non ha il permesso di esecuzione, il comando va preceduto da
$chmod a+x calcnav-x.y.x.py
Se il programma parte, sul vostro computer è già
installato l'interprete python... ottimo! Potete passare al punto 3)
2) Se il programma non è partito è necessario installare l'interprete python. Andate sul sito www.python.org, scaricate una versione di python posteriore alla 2.2 adatta al vostro sistema operativo (sezione downloads, seguite le indicazioni che vi troverete) e installatela sul vostro computer (si raccomanda di installare anche le librerie opzionali, in particolare il modulo “tkinter” che serve per far funzionare l'interfaccia grafica di calcnav). Dopo che l'installazione è completata e andata a buon fine verificate che il programma parta, con la procedura illustrata al punto 1).
3) Andate sul sito www.blender3d.org e scaricate una versione di Blender adatta al vostro sistema operativo. Installatela sul vostro computer.
A questo punto siete pronti per usare Calcnav. Poiché il sistema più semplice per apprendere è quello di seguire un esempio, verrà ora mostrato il modo di modellare e ed eseguire la verifica di stabilità di uno scafo: decidiamo di realizzare una piccola nave in ferro lunga 20 metri.
2 - ESEMPIO DI USO DEL PROGRAMMA ADOPERANDO LA MODELLAZIONE AUTOMATICA:
Lanciate “calcnav-x.y.z.py”: si apre la schermata del programma, contenente una finestra principale, predisposta per indicare le dimensioni principali dello scafo, ed una colonna a destra. Notate come insieme al programma si apra una finestra che riporta dati ed operazioni (nei sistemi Linux è la stessa shell da cui si è lanciato il programma, nei sistemi windows è una finestra aggiuntiva). In questa finestra il programma scrive dati accessori e altre informazioni che può essere utile tener d'occhio.
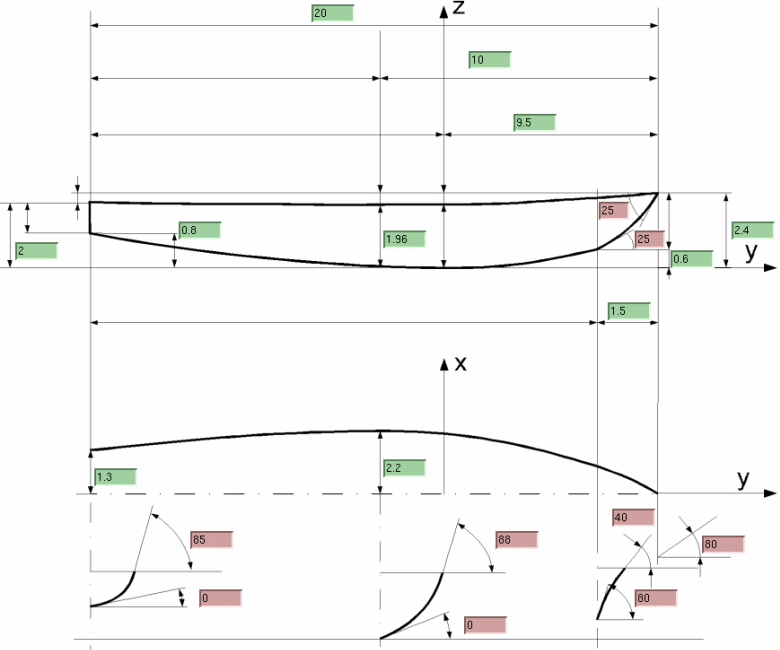
Si inizia stabilendo le dimensioni di massima, ed inserendole nelle rispettive caselline; le quote del disegno indicano chiaramente il significato dei valori da introdurre. Nelle caselline colorate in verde vanno misure lineari, espresse in metri, in quelle colorate in rosso vanno misure angolari in gradi.
Si ricordi di usare il punto al posto della virgola: attualmente il programma non possiede un sistema di controllo della correttezza dei valori immessi nelle caselle, per cui occorre fare attenzione ad inserire valori numerici correttamente interpretabili.
Come appare chiaro il programma assume un sistema di riferimento costituito da tre assi ortogonali come indicati nella finestra del programma: y asse orizzontale sul piano mediano, x asse trasversale, z verticale. L'origine si trova in corrispondenza della sezione di massimo pescaggio, nel punto più basso (chiglia) della sezione.
Pertanto si scelgono:
lunghezza fuori tutto: 20 m
sezione maestra (massima larghezza) a 10 m dall'estrema prua
sezione di massimo pescaggio (non necessariamente coincidente con quella
maestra) a 9,5 m dall'estrema prua. Si osservi che si potrebbe
tranquillamente stabilire la sezione massimo pescaggio a poppa di
quella maestra, imponendo la seconda quota maggiore della prima: il
disegno della schermata non rappresenta un vincolo in questo senso, ma
serve solo da rappresentazione schematica.
Altezze di costruzione relative al piano x-y (su cui si trova il punto più basso dello scafo):
poppa: 2 m
chiglia della sezione poppiera: 0,8m
sezione maestra: 1,96 m (4 cm meno della poppa per conferire una certa
insellatura)
base della ruota di prua: 0,7 m
estrema prua: 2,4 (anche qui l'aumento rispetto alla sezione maestra
conferisce l'insellatura)
Base della ruota di prua distante in pianta 1,5 m dall'estremità
Semilarghezza dello specchio di poppa: 1,3 m
Semilarghezza massima: 2,2 m
Angoli formati dalle tangenti alle estremità delle mezze sezioni
rispetto al piano orizzontale:
poppa: in chiglia 0°, sul bordo 85°
sezione maestra: in chiglia 0°, sul bordo 88°
sezione in corrispondenza della base della ruota di prua: in chiglia 80°,
sul bordo 40°
sezione d'estremità: 80° (quest'ultimo è un valore limite,
attribuito ad una curva di lunghezza nulla, ma che serva per impostare con maggior
precisione l'andamento dell'angolo lungo la ruota di prua).
Come si vede, questi dati danno luogo ad uno scafo a fondo piatto con la
prua svasata. È chiaro che cambiando i parametri si possono ottenere forme
notevolmente diverse.
Infine i due angoli che definiscono la forma della ruota di prua, che può
risultare convessa, concava, concavo-convessa o dritta. Tenendo
presente la mutua posizione del punto di base e del punto estremo
della ruota di prua, definite dalle altezze e dalle distanze
precedentemente introdotte, si scelgono qui gli angoli di 25° e
25°, che daranno luogo ad una prua “da veliero”.
Il risultato dev'essere una schermata come la seguente:
Ora occorre indicare gli altri parametri necessari alla definizione dello scafo e all'esecuzione del calcolo, inserendoli negli spazi della colonna a destra.
Parametri di approssimazione:
Il programma approssima lo scafo per punti, impiegando il numero richiesto di sezioni, su ciascuna delle quali traccia il numero richiesto di punti. Naturalmente aumentando il numero complessivo di punti (cioè aumentando il numero di sezioni e/o il numero di punti per ogni sezione) migliora la precisione del risultato, ma crescono anche i tempi di calcolo: eseguite alcune prove per rendervi conto della velocità complessiva del calcolo sul vostro computer.
Si indichino allora questi parametri nelle apposite caselle sulla
destra:
numero di sezioni da poppa alla base della ruota di prua: 40
numero di sezioni lungo la ruota di prua: 40
In genere conviene rendere più fitte le sezioni lungo la ruota di
prua, che è la zona dello scafo dalla geometria più
complessa e richiede dunque una migliore approssimazione: a questo
scopo il programma consente di specificare separatamente i due
valori. In questo caso si è scelto un valore decisamente elevato
per rendere in dettaglio la sagoma concavo-convessa che si è
scelta per la prua.
numero di punti per ogni mezza sezione: 20
Per ragioni di comodità di calcolo il numero di punti su ogni
sezione completa deve essere dispari; il programma chiede di indicare
il numero di punti sulla mezza sezione, che poi verrà
convenientemente adattato. In questo caso ogni sezione comprenderà
39 punti, cioè saranno presenti 20 punti sulla mezza sezione
dal bordo alla chiglia compresa.
Lungo la prua questo numero di punti viene ridotto gradualmente fino all'unico punto che costituisce l'estremità dello scafo.
spessore dello scafo [mm]: 8
Questa è la distanza che separerà la superficie esterna da
quella interna: il volume compreso fra le due superfici costituirà
il volume proprio dello scafo, che, moltiplicato per la densità
del materiale di costruzione, darà la massa dello scafo.
Con i dati finora introdotti è già possibile ottenere
il disegno dello scafo; il sistema è molto rapido, ma può comunque risultare
comoda l'anteprima delle tre sezioni fondamentali: poppa (P), sezione maestra (M)
e base della ruota di prua (R). Premendo il pulsante "Ginocchio sezioni"
compare una finestra accessoria in cui si vedono le tre mezze sezioni: esse sono
composte da due archi di curva raccordati fra loro in modo da rispettare i valori
imposti. Il programma provvede automaticamente a trovare il punto di raccordo fra
i due archi che compongono ogni mezza sezione, e quindi a definire il ginocchio:
tale risultato è valido nella maggior parte dei casi, ma può risultare scorretto,
specialmente nel caso di vistose variazioni della forma della sezione lungo lo scafo
(ad esempio: poppa larga e piatta e sezione maestra profonda e affilata, o viceversa).
In questi casi è possibile intervenire selezionando la "scelta del ginocchio manuale"
e ritoccando il parametro che definisce il punto di raccordo per le tre sezioni; esso
può variare fra 1 e 99, spostando il punto di raccordo da una posizione prossima alla chiglia
(valore 1) fino ad una prossima al bordo (valore 99), e modificando di conseguenza
le tre sezioni.
Dopo aver modificato i parametri, premendo il pulsante "ridisegna" si vede il risultato
della modifica. In genere dopo pochi tentativi di ottiene la forma desiderata: ad esempio,
le immagini seguenti mostrano il risultato di una correzione di questo tipo su uno
scafo piatto con una lieve sporgenza in chiglia nella sola regione poppiera:
nella prima si vede come la resa automatica abbia comportato un cattivo andamento
delle linee, nonostante sia stata rispettata la continuità dei parametri.
Più avanti la sezione "funzionamento del programma" illustra in dettaglio in cosa consiste il calcolo del punto di raccordo.


Ora si vede lo stesso scafo, differente dal primo caso solo per l'impostazione manuale del parametro di raccordo.


È bene rimarcare che l'impostazione del ginocchio (punto di raccordo) avviene conservando tutti i parametri
già impostati nella finestra principale di Calcnav, cioè angoli e posizione di chiglia
e bordo, per cui modifiche diverse dalla posizione del ginocchio vanno apportate in quella schermata.
Chiudendo la finestra le impostazioni date, naturalmente, si conservano
e possono essere ulteriormente corrette in un secondo tempo.
Iniziano ora i parametri necessari alla valutazione delle grandezze dinamiche.
Approssimazione sul volume [%]: 0.1
Per ogni valore di sbandamento assegnato il programma esegue la ricerca della posizione del piano di galleggiamento, cioè trasla il piano di galleggiamento, inclinato dell'angolo richiesto, perpendicolarmente a sé stesso fino a che il volume immerso effettivo (quello che il piano taglia sullo scafo) sia pari al volume immerso richiesto, cioè alla massa dello scafo carico divisa per la densità dell'acqua. Questa operazione viene effettuata per tentativi, in base a un opportuno algoritmo di ottimizzazione, e si arresta quando la differenza fra i due volumi (immerso effettivo ed immerso richiesto) diventa più piccola di un valore minimo ritenuto accettabile. Questo valore minimo è la grandezza da indicare nella casella “Approssimazione sul volume”, da esprimere in percentuale del volume immerso richiesto. In pratica, assegnando il valore 0,1, si permette al programma di accettare come valido il calcolo eseguito con il piano di galleggiamento che taglia sullo scafo un volume immerso che può differire al massimo dello 0,1% dal volume immerso richiesto.
Si tenga presente che più l'approssimazione sul volume è piccola, più diviene lento il calcolo; inoltre l'approssimazione dev'essere commisurata all'approssimazione con cui si disegna lo scafo: più quest'ultimo è preciso (maggior numero di sezioni e di punti per sezione impiegato), più si può spingere (ridurre) l'approssimazione sul volume; in caso contrario, oltre un certo limite, l'algoritmo che ricerca il piano di galleggiamento non può convergere. In questo caso occorre bloccare l'esecuzione del programma (Ctrl-C nei sistemi Unix) e ritentare dopo aver aumentato il numero di punti e sezioni e/o aumentato il valore dell'approssimazione sul volume.
densità materiale scafo: 7600
Si sceglie il valore (in kg/m3) di un generico acciaio.
densità del fluido: 1030
Si tratta della densità del fluido in cui lo scafo galleggia, ancora in kg/m3: è
preimpostato il valore 1030 dell'acqua di mare; se necessario è possibile cambiarlo.
Premendo il pulsante “imposta masse accessorie” si apre una
finestra che consente di specificare i dati di un certo numero di
masse accessorie con cui si intende caricare lo scafo: è
possibile in questo modo simulare la presenza di sovrastrutture,
propulsori, impianti, passeggeri, carburante. Per ogni massa che si
vuole aggiungere occorre specificarne il valore in kg. Le altre
grandezze, se non specificate, vengono assunte pari a 0
dal programma. Si tratta delle coordinate x, y e z del baricentro
della massa aggiuntiva e dei momenti d'inerzia centrali Ix, Iy e Iz.
Si noti che un valore di x diverso da 0 colloca la massa in posizione
asimmetrica e rende lo scafo sbilanciato.
Vi siete accorti che manca la possibilità di inserire i momenti centrifugo-composti? Beh, si suppone che gli assi x, y e z siano principali d'inerzia per le masse. Se questo proprio vi dà fastidio, si può pensare di adeguare il programma...
Una volta specificate le grandezze desiderate per una massa, si sceglie
il pulsante “aggiungi massa” ed essa viene collocata
nell'elenco visibile superiormente nella stessa finestra. Il numero
progressivo a sinistra consente di cancellare le masse che si
volessero eventualmente eliminare: per far questo si scrive il numero
nella casella a fianco della scritta “elimina massa n.” e
si preme il pulsante corrispondente. Notare che l'elenco parte dal
numero 0.
In questo esempio immettiamo una massa di 800 kg nella posizione y=-3 m
e z = 1 m e un'altra di 1000 kg nel baricentro. Quando si preme “aggiungi
massa” nella finestra principale del programma, a fianco del pulsante “imposta
masse accessorie” viene aggiornato un indicatore che segnala il
numero delle masse introdotte fino a quel momento.
La finestra delle masse accessorie si presenta dunque come nella figura:

Ora si può chiudere la finestra delle masse accessorie; l'indicatore conserva il numero corretto, segnalando che il programma terrà conto delle masse introdotte.
Impostazioni del diagramma di stabilità:
Come già spiegato, il diagramma si ottiene imponendo un angolo di sbandamento e valutando la coppia raddrizzante con cui reagisce lo scafo; questo diagramma viene ricostruito per punti, dall'angolo 0 fino al valore massimo richiesto procedendo ad intervalli regolari. L'intervallo di valutazione è la differenza in gradi fra due angoli successivi per i quali si calcola la coppia raddrizzante. Il numero di punti stabilisce di quanti valori, a partire dallo 0 compreso, si comporrà il diagramma.
In questo esempio:
intervallo di valutazione [°]: 3
numero di punti: 8
In pratica il programma eseguirà il calcolo per otto volte, a
intervalli di 3°, e cioè per i seguenti angoli:
0, 3, 6, 9, 12, 15, 18, 21
Quando si spinge il calcolo ad angoli elevati, bisogna sapere che il programma fornisce risultati corretti fintanto che lo scafo interseca il piano di galleggiamento solo con la superficie esterna; qualora il bordo vada sotto acqua avviene una sovrastima del volume immerso. Si tratta di una limitazione che potrà essere corretta in futuro modellando anche la coperta.
Ora la colonna destra della schermata si presenta come nella figura:

Ora è possibile far partire il calcolo. Innanzitutto si salvano i dati introdotti, dal momento che potrebbe esser comodo riadoperarli in seguito, variando qualche parametro per vedere come cambiano le caratteristiche della nave. Si preme allora il pulsante “salva i dati”: il programma scrive un documento di testo, di nome “calcnav.dati”, contenente tutte le grandezze introdotte. Tale documento è fatto in modo da poter essere aperto ed eventualmente modificato a mano con qualunque programma di elaborazione di testi (un “blocco note” va benissimo) e si trova nella stessa cartella del programma: provate a cercarlo ed aprirlo.
Volendo, nella casella in basso “note del documento dati” è possibile inserire del testo a piacere, che viene riportato in calcnav.dati e può servire a ricordare informazioni o dettagli sullo scafo che si sta studiando.
Il pulsante “Carica i dati”, invece, serve ad aprire un documento “calcnav.dati” già presente e caricare tutti i dati in esso contenuti nel programma, in modo da poterli modificare e/o eseguire i calcoli.
Come si vede non sono disponibili procedure per aprire e salvare documenti di nome arbitrario (i classici "apri" e "salva con nome"): finora non si è presentata la necessità di affrontare le complicazioni relative. Si possono comunque archiviare più documenti di dati usando il sistema operativo per cambiarne il nome.
Si prema il pulsante “Solo disegno”: il programma scrive due documenti di dati, contenenti le coordinate dei punti della superficie esterna e della superficie interna. Essi si chiamano “sup_scafo_est” e “sup_scafo_int” e si trovano nella stessa cartella del programma. È ora possibile vedere lo scafo: i due documenti vanno copiati nella cartella di Blender. Insieme ad essi si copi (una volta per tutte) il documento “scafo3d.blend” fornito con il pacchetto calcnav. Esso contiene le istruzioni per Blender che gli permettono di importare i dati delle due superfici.
Si faccia partire Blender e si apra scafo3d.blend (nel modo consueto, menu File -> open, scegliere scafo3d.blend dalla cartella di Blender). La schermata del programma è divisa in due verticalmente, e nella metà di sinistra compare il testo dello script di importazione dei dati (si tratta di un piccolo programma scritto anch'esso in python). Si porti la freccia del mouse su quella metà (è sufficiente che la freccia stia sopra il testo, in un punto qualunque), si lasci il mouse e si premano sulla tastiera i pulsanti Alt P contemporaneamente.
Questa combinazione di pulsanti dà a Blender l'ordine di eseguire lo script, e dopo qualche istante nella metà destra della schermata compare il disegno delle due superfici, interna ed esterna. Portate la freccia del mouse nella metà destra, tenete premuto il tasto centrale e mouvete il mouse: osservate lo scafo in assonometria da diverse angolature. Senza toccare il mouse, i pulsanti 1 2 3 6 9 8 7 4 del tastierino numerico muovono analogamente la figura. Il 5 fa passare dall'assonometria alla prospettiva e viceversa.


Magari siete abituati a usare il vostro programma di disegno 3d preferito, e vorreste vedere il risultato con quello? Allora, tenendo il puntatore del mouse nel riquadro di Blender contenente il disegno, premete due volte il pulsante A della tastiera: in questo modo vengono selezionate entrambe le superfici disegnate (diventano entrambe colorate in viola); ora andate sul menu file e scegliete “esporta”: il formato dxf dovrebbe andar bene per la maggior parte dei programmi di disegno assistito; seguite le indicazioni (esporta tutto) e otterrete le due superfici dello scafo in formato dxf.
Ora vi siete fatti un'idea di massima dello scafo di cui avete stabilito i dati; naturalmente Blender può fare molto e molto di più nella rappresentazione, ma per ora queste immagini possono essere sufficienti.



Tornate allora alla schermata di calcnav. Se nel frattempo l'avevate chiuso, fatelo ripartire, quindi scegliete “carica i dati” per fargli aprire e leggere il documento calcnav.dati precedentemente salvato. Premete il pulsante “Calcolo”: poiché il tempo di calcolo può essere lungo (a seconda del numero di punti impostato, del numero di angoli richiesto e delle capacità del computer con cui si lavora in genere si va da qualche secondo a qualche minuto), è interessante tenere d'occhio la finestra accessoria (la shell), nella quale il programma scrive informazioni sullo stato di avanzamento del calcolo. Proprio in essa si può verificare facilmente se per caso l'approssimazione richiesta sul volume sia stata impostata ad un valore eccessivamente piccolo (come già spiegato in precedenza): si vedono infatti le iterazioni seguite dal programma nella ricerca del piano di galleggiamento, per ognuna delle quali viene fornito il volume immerso approssimato e la posizione del piano di galleggiamento corrispondente; tali valori devono cambiare oscillando in un intervallo sempre più piccolo fino a rientrare nell'intervallo di approssimazione richiesto. Se ciò non accade l'algoritmo non converge, e il programma stesso segnala la possibilità (non la certezza, per ragioni che vengono esposte nel paragrafo 4.4.1) che questa circostanza sia verificata scrivendo un avvertimento fra una riga e l'altra. Perciò, se si riscontrano i sintomi della non convergenza delle iterazioni (tempo di elaborazione eccessivamente lungo, reiterati avvertimenti del programma, e soprattutto ritorno a valori del volume già trovati in precedenza) occorre arrestare l'esecuzione e ritentare avendo cura di suddividere più finemente lo scafo e/o aumentare l'approssimazione sul volume richiesta.
Alla fine viene visualizzato il diagramma di stabilità, riportante in ascissa i gradi e in ordinata i bracci (in m) ed i momenti (in Nm)

Non esiste per ora un sistema per salvare automaticamente questa immagine: se
proprio serve la si può catturare dallo schermo con uno dei sistemi
consueti; questa mancanza non è così grave in quanto, contemporaneamente
al diagramma, viene prodotto un documento “dati.txt”, collocato
nella cartella del programma, che contiene tutti i risultati,
compresi i valori del diagramma di stabilità tabulati. Inoltre
è presente la posizione del piano di galleggiamento, definita
come valore di z per il quale il piano interseca l'asse z stesso. Chiamando
“q” tale valore e φ l'angolo di sbandamento
sull'asse di rollio, il piano di galleggiamento rispetto agli assi x,
y, z dello scafo si scrive come
z = tanφ*x + q
Il testo di "dati.txt" è il seguente:
Risultati del calcolo di stabilità Documento generato automaticamente da scafocalc2 La superficie dello scafo è approssimata da 4600 triangoli Lo scafo è approssimato da 13743 elementi tetraedrici Approssimazione tollerata sul volume immerso: 0.1%, pari a 0.00824600242444 m^3 A - Grandezze relative al solo scafo: Volume proprio (somma dei volumi dei tetraedri):0.880708223312 m^3 Area totale della sup. esterna: 110.74133634 m^2 Volume proprio approssimato (Atot*spessore): 0.885930690719 m^3 Massa: 6693.38249717 kg Coordinate del baricentro [m]: -0.00101083876105 -1.30727809961 0.907758683138 Momenti d'inerzia centrali: Ix (beccheggio)= 187602.561689 kg*m^2 Iy (rollio)= 13731.337748 kg*m^2 Iz (imbardata)= 196468.096573 kg*m^2 B - Grandezze relative allo scafo carico: Massa: 8493.38249717 kg Volume immerso: 8.24600242444 m^3 Coordinate del baricentro [m]: -0.000796612006224 -1.31279997746 0.809568635778 Momenti d'inerzia centrali: Ix (beccheggio)= 192352.470162 kg*m^2 Iy (rollio)= 14597.1477299 kg*m^2 Iz (imbardata)= 200469.061025 kg*m^2 Tabella di stabilità: angolo braccio[m] momento raddrizzante [N*m] piano di gall.[m](*) xC [m] yC [m] zC [m] 0.0° 0.000796612006224 66.3737779175 0.479791040577 3.35162789613e-18 -1.22250276446 0.315007041932 3.0° 0.101557932951 8461.81533139 0.477160374776 0.126626613285 -1.23299667527 0.318688845223 6.0° 0.200261075794 16685.7693161 0.468914125445 0.251126271432 -1.26442326281 0.328534607741 9.0° 0.296440863858 24699.4771729 0.454751088048 0.373027771033 -1.30315510055 0.344318726293 12.0° 0.388791730357 32394.1589699 0.435394581931 0.490883998824 -1.36572290581 0.366378168272 15.0° 0.477663276115 39798.9434763 0.409815250937 0.605119083676 -1.44060318278 0.393809653064 18.0° 0.558040276137 46495.9617329 0.378647931392 0.710884916394 -1.52208359145 0.425094379872 21.0° 0.632922138486 52735.1246664 0.340939802204 0.81120319101 -1.60528257014 0.460360554842 (*)Per il significato di questa grandezza si veda la guida Altezza metacentrica: - Valutazione 1: § momento d'inerzia dell'area: 20.0902774886 m^4 § I / V immerso= r =2.43636570238 m § zG - zC = a =0.494561593846 m § GM = r-a =1.94180410853 m - Valutazione 2: § GM = b/sen(phi) =1.94050018842 m § GM = interp.(b/sen(phi))=1.98999978589 m Periodo dell'oscillazione trasversale: 14.7389410405s
Come si vede, dopo il riassunto dei dati dell'approssimazione geometrica impiegata, vi si trova una prima sezione che riporta le grandezze relative al solo scafo, una seconda con le stesse grandezze, ma relative alla nave con le masse aggiuntive stabilite, quindi la tabella contenente i risultati del calcolo di stabilità. I dati di quest'ultima sono separati da tabulazioni per renderne più semplice l'eventuale trasporto in un foglio elettronico. Infine è riportato il calcolo dell'altezza metacentrica, eseguito
fondamentalmente in due modi diversi, che portano a tre risultati finali. Il primo, indicato con "Valutazione 1" si ottiene con la
formula
GM=momento d'inerzia centrale della sezione al galleggiamento / volume immerso - differenza di altezza fra baricentro e centro di spinta
generalmente scritta in letteratura come
GM=I/V-(zG-zC).
Il secondo sistema (valutazione 2) produce più semplicemente il braccio raddrizzante diviso per il seno dell'angolo di
sbandamento, calcolato estrapolandone il valore per l'angolo nullo. Poichè il programma ha già calcolato il valore del braccio
in corrispondenza di diversi angoli, è immediato (e interessante) eseguire l'estrapolazione partendo dal solo primo valore disponibile dopo 0°, o dai primi due, e questi due risultati vengono riportati. Come si vede, le tre valutazioni forniscono risultati molto vicini fra loro. Nel caso in cui ciò non accadesse, sarà opportuno ripetere il calcolo aumentando la definizione dello scafo
e/o infittendo i punti del diagramma di stabilità.
Naturalmente il programma riporta i numeri così come risultanti dal calcolo, ma le cifre significative vengono lasciate al buon senso dell'utilizzatore!
Nella stessa cartella il programma produce un documento “grafico.svg”
che contiene il disegno del diagramma in un formato di grafica
vettoriale: lo si può visualizzare con diversi programmi, ad
esempio batik (liberamente scaricabile da
http://xml.apache.org/batik).
Questo grafico è un retaggio delle prime versioni di Calcnav, funzionanti interamente da riga di comando senza
interfaccia grafica; pertanto i parametri che lo definiscono (dimensione della finestra, posizione dell'origine degli
assi sullo schermo, scala degli assi) si trovano all'inizio dello script scafocalc2; volendo è possibile modificarli
a mano: non se ne è automatizzata la modifica poiché si è preferito far rilasciare il grafico direttamente da Calcnav,
anche se non c'era ragione di eliminare la produzione di questo documento svg.
In alternativa, copiando la tabella di stabilità presente in
dati.txt in un foglio elettronico sarà immediato ottenere il
relativo grafico.
Ora che disponete dei risultati del calcolo potete decidere se la vostra
nave va bene o se è il caso di cambiarne la geometria o la
distribuzione dei pesi.
Potete anche cambiare i dati di approssimazione per verificare quanto essi
influiscano sul risultato: aumentando il numero di punti e riducendo l'approssimazione
sul volume (si ricordi che il secondo parametro non va ridotto troppo se non viene
contemporaneamente aumentato il primo), i risultati del calcolo saranno più
precisi, ma oltre un certo grado la precisione non aumenta sensibilmente, mentre
il tempo di calcolo sì!
C'è però ancora un quesito che può risultare molto importante per il progettista, e concerne la disposizione che la nave prenderà sull'asse di beccheggio, ovvero se i volumi di prua e poppa siano bilanciati e se rimangano tali a seguito degli sbandamenti. L'assetto sull'asse di beccheggio può diventare molto importante, specialmente per scafi particolari come quelli di certe barche a vela dalla prua molto svasata e dalla poppa larga e piatta, che, a seguito dello sbandamento in rollio, tendono ad immergere la prua e a far emergere la poppa, talvolta riducendo drasticamente la capacità di governo della pala del timone. In questo caso, calcnav dispone di un algoritmo di calcolo aggiuntivo, che, insieme alla ricerca della posizione del piano di galleggiamento, esegue la ricerca dell'angolo di beccheggio preso dalla nave, individuabile come l'angolo in corrispondenza del quale la coppia che produce tale angolo si annulla. Purtroppo l'algoritmo che governa questo calcolo non è efficiente come quello che serve alla stabilità trasversale, e può succedere, sebbene in casi molto sporadici, che la convergenza sia molto lenta e richieda numerosi passaggi e molto tempo.
In maniera del tutto analoga a quanto già esposto per la ricerca del piano di galleggiamento, anche qui occorre indicare al programma il valore minimo ritenuto accettabile di una grandezza correlata all'angolo di sbandamento: qui si è scelto il braccio di beccheggio. Si consideri l'asse definito come intersezione fra il piano di galleggiamento ed il piano mediano dello scafo: proiettando su tale asse la distanza fra centro di gravità della nave e baricentro del volume immerso si ottiene questo braccio, che non è altro che la lunghezza della “leva” con cui il peso della nave e la spinta di galleggiamento generano l'inclinazione della nave stessa sull'asse di beccheggio. Questo braccio deve risultare nullo una volta che si è individuato il valore corretto dell'angolo di beccheggio: come per il piano di galleggiamento, si deve stabilire il valore massimo accettabile per il braccio di beccheggio, sotto il quale la coppia può essere trascurata. Tale valore va indicato nella casellina apposita, come valore percentuale rispetto alla lunghezza fuori tutto dello scafo.
In questo caso assumiamo:
appross. sul braccio di beccheggio [%Lft]: 0.1
cioè indichiamo al programma di arrestare la ricerca una volta che avrà
individuato un angolo tale che il braccio di beccheggio risulti pari
allo 0,1% della lunghezza fuori tutto dello scafo. In questo caso,
essendo lo scafo di 20 m, si riterrà trascurabile una coppia
generata da un braccio al più di 2 cm.
Ora si può scegliere il pulsante “Calcolo beccheggio”. Il tempo di calcolo può risultare sensibilmente più lungo rispetto al calcolo normale: in questo caso è un'ottima idea verificare l'andamento delle operazioni nella finestra accessoria.
Al termine viene prodotto il consueto “dati.txt” che riporta, oltre alle normali informazioni, anche gli angoli sull'asse di beccheggio in corrispondenza degli angoli imposti sull'asse di rollio.
Infine, premendo il pulsante "esporta dati", si apre una finestrella che permette di salvare la modellazione dello scafo nei due formati "stl" ed "fbd". Premendo uno dei pulsanti verrà prodotto, nella stessa cartella di calcnav, il documento scafo.stl o scafo.fbd, adoperabili con programmi appositi. Per ulteriori dettagli su questi formati, e soprattutto a proposito dei parametri richiesti per produrre il documento "fbd", si veda il capitolo "Formati di esportazione" di questa guida.
Al termine dell'esposizione del modo di adoperare il programma, risulterà chiaro che i parametri che definiscono lo scafo possono essere stabiliti per approssimazioni successive, verificando di volta in volta il risultato delle modifiche nel disegno fino a raggiungere la forma più vicina a quella desiderata. Per questo è decisamente più comodo far sì che calcnav stesso copi i documenti delle superfici ogni volta che li produce. A questo scopo la casella in basso, "cartella per i disegni", contiene il nome della cartella in cui si desidera che tutti i disgeni prodotti vengano copiati (duplicati), in modo da poterli aprire rapidamente con il programma di disegno. Per modificare l'impostazione basta scrivere nella casella il nome della cartella desiderato e premere il vicino pulsante salva impostazione cartella; il programma trascrive il nome indicato nel documento allegato "impostazioni", in modo che rimanga sempre disponibile.
Ad esempio per un sistema Unix/Linux può essere:
/home/utente/blender-2.37a-linux-glibc2.2.5-i386-static/
per un sistema windows invece:
C:\programmi\blender-2.37a\
Naturalmente ognuno deve scrivere il percorso ed il nome della cartella come
si trovano nel suo computer. In questo modo calcnav copia nella cartella richiesta
i documenti prodotti: così si può tenere aperto Blender, cambiare il disegno con
calcnav e vedere le modifiche semplicemente andando nella schermata di Blender e
premendo "Alt P".
Naturalmente, se non si dà questa impostazione, il programma funziona ugualmente.
Da ultimo è bene avvertire che il programma genera numerosi documenti
provvisori che servono a trascrivere risultati parziali durante le varie
operazioni: essi si trovano nella cartella "temp" (prodotta automaticamente
alla partenza del programma), che alla fine dei calcoli può risultare
ingombrante (vari Mb), ma si può eliminare in blocco senza alcuna perdita di dati.
3 - ESEMPIO DI USO DEL PROGRAMMA IMPORTANDO UN DISEGNO PRODOTTO ESTERNAMENTE:
Si raccomanda di leggere la sezione precedente "esempio di uso con modellazione automatica" prima di
iniziare la presente, così da aver chiaro il funzionamento generale del programma ed alcune necessità derivanti
dai calcoli che vengono eseguiti.
Si suppone ora di voler eseguire il calcolo di stabilità di un galleggiante che non si potrebbe richiedere
al modellatore automatico: in questo caso una specie di tinozza! Usando un programma di disegno assistito (in questo
caso Blender), non è difficile ottenere un disegno come il seguente, cioè un tronco di cono.

Il disegno deve rappresentare la superficie esterna del galleggiante, cioè quella che nel corso della simulazione
(quindi in seguito allo sbandamento) potrebbe venir bagnata dall'acqua. Questo punto è importante, perché qualora
si rappresentasse anche la superficie interna (quella cioè che è divisa rispetto all'esterna dallo spessore delle pareti)
il programma considererebbe come volume galleggiante solo quello compreso fra le due pareti: in altri termini verrebbe
valutata la stabilità della tinozza o della barca piene d'acqua! Inoltre, dato il funzionamento del programma, verrebbe
sovrastimato in maniera inaccettabile il peso proprio dello scafo.
Una volta eseguito il disegno occorre esportarlo nel formato stl non compresso, che approssima la superficie
con triangoli, in modo da permettere a calcnav di importarlo.
Blender esporta i disegni in un formato stl "binario" non adoperabile direttamente; per ottenere l'stl "semplice" è possibile usare lo script "blend2stl.py" che è disponibile in questo sito alla pagina "vari script...". In genere altri programmi consentono di ottenere un stl tranquillamente adoperabile.
A partire dal disegno della superficie esterna in stl calcnav ricostruisce le caratteristiche dello scafo per adoperarle nel calcolo. È importante avere due avvertenze:
1) suddividere le superfici del galleggiante in triangoli sufficientemente piccoli, anche se si tratta di grandi superfici piane, che di per sé sarebbero adeguatamente rappresentabili con pochi triangoli; infatti calcnav usa questa discretizzazione per individuare la superficie immersa per ogni angolo di sbandamento, e dunque il risultato migliora se le particelle di superficie sono piccole, mentre con porzioni troppo grandi può succedere addirittura di non ottenere un risultato (cioè l'algoritmo può non convergere, come già spiegato a proposito dell'approssimazione sul volume immerso nella sezione precedente).
2) l'stl contiene la definizione del vettore normale ad ogni superficie triangolare che forma il disegno; tali normali devono essere rivolte esternamente alla superficie (cioè verso l'acqua); in questo modo calcnav valuta correttamente il volume immerso (anche in caso di rientranze o sporgenze inusuali), e inoltre ricostruisce (in via approssimata) lo spessore dello scafo dalla parte opposta alla superficie bagnata.
In genere i programmi di disegno consentono di assolvere molto facilmente a queste due condizioni. Nelle immagini successive, la tinozza suddivisa ed esportata in stl (24064 triangoli) con Blender, e la stessa con i vettori normali rappresentati da linee azzurre.


L'inconsueto galleggiante di questo esempio ha un diametro di due metri.
A questo punto conviene salvare il documento stl nella stessa cartella di calcnav. Si fa partire
quindi calcnav stesso e si introducono i dati relativi alla simulazione da effettuare, tenendo conto che la geometria
del galleggiante è già definita dal documento stl preparato. Si capisce quindi che si omettono tutti i dati della
finestra di sinistra (quella con il disegno dello scafo), mentre nella colonna di destra ne occorrono solo alcuni.
Perciò si inseriscono i seguenti:
spessore dello scafo [mm]: 10;
approssimazione sul volume [%]: 0,1
come già rilevato, e in maniera del tutto analoga a quanto spiegato nella sezione precedente relativamente a questo comando,
questo valore deve essere commisurato alla finezza con cui si è discretizzato l'oggetto; in questo caso dunque, più
sono i triangoli che compongono l'stl, più l'approssimazione tollerata può essere spinta a valori bassi.
densità materiale scafo [kg/m^3]: 600
la tinozza è fatta di legno!
densità fluido [kg/m^3]: 1000
imposta masse accessorie: come già spiegato nella sezione precedente si imposta una massa di 150 kg al centro della tinozza,
in questo caso all'altezza di 70 cm dal fondo.
intervallo di valutazione dello sbandamento [°]: 3
numero di punti del diagramma: 8
Come già chiarito, gli ultimi due dati stabiliscono che si otterranno le caratteristiche di stabilità in corrispondenza
degli angoli 0°, 3°, 6°, 9°, 12°, 15°, 18°, 21°.
Perciò ora la colonna di destra si presenta come nell'immagine seguente:

Si può premere ora il pulsante "importa dati": si apre una finestrella accessoria contenente:
- un campo in cui indicare il nome (e l'eventuale posizione) del file stl da aprire: è preimpostato il nome
"scafo.stl";
- un campo in cui indicare la scala con cui l'stl è rappresentato: calcnav infatti lavora in metri e, se il disegno
è predisposto in unità diverse, occorre segnalarlo al programma, altrimenti si lascia il valore "1" preimpostato.
La scala va indicata in metri/unità del disegno: ad esempio, se lo scafo è stato disegnato in millimetri, la scala
da impostare è 0,001, se è in piedi, la scala è 0,3048;
- il pulsante per far partire l'acquisizione dell'stl, che finalmente può avvenire;
- il pulsante per far partire solo il calcolo di stabilità (nel caso in cui l'acquisizione del documento stl sia già avvenuta in precedenza).

Premendo il pulsante "importa" il programma trova la superficie, legge l'stl e produce i due documenti "datiscafosup" e "datiscafovol"; quindi esegue il calcolo di stabilità: da qui in poi il funzionamento prosegue esattamente come descritto nella sezione precedente.
Invece, premendo il pulsante "calcola" il programma si limita ad eseguire il calcolo, ricercando i documenti
"datiscafosup" e "datiscafovol" che si suppone siano già stati prodotti in precedenza; in pratica questo pulsante esegue quanto fa il precedente, ad eccezione dell'operazione iniziale di importazione dell'stl: ciò risulta comodo nel caso in cui si vogliano eseguire più simulazioni sullo stesso scafo cambiando le masse, ma risparmiando il tempo dell'acquisizione iniziale che può diventare non trascurabile.
È risultato opportuno far generare un documento contenente la sequenza delle operazioni svolte durante tale fase, che può servire per risolvere eventuali disfunzioni che si verifichino nel corso dell'acquisizione dell'stl: si tratta del documento "stl2calc.log" che viene salvato (e sovrascritto ogni volta) nella sottocartella "temp" creata dal programma all'avvio nella propria cartella; esso può essere eliminato senza preoccupazioni.
Si ottengono quindi il diagramma di stabilità e il documento "dati.txt" che contiene tutti i dati relativi
al galleggiante. La posizione del piano di galleggiamento, naturalmente, è data nello stesso sistema di
riferimento in cui sono espressi i punti dell'stl.
Questo è il diagramma ottenuto:

Mentre il seguente è il testo del documento "dati.txt" prodotto:
Risultati del calcolo di stabilità Documento generato automaticamente da scafocalc2 La superficie dello scafo è approssimata da 24064 triangoli Lo scafo è approssimato da 72192 elementi tetraedrici Approssimazione tollerata sul volume immerso: 0.1%, pari a 0.0001862053799 m^3 A - Grandezze relative al solo scafo: Volume proprio (somma dei volumi dei tetraedri):0.0603422998337 m^3 Area totale della sup. esterna: 6.03422998338 m^2 Volume proprio approssimato (Atot*spessore): 0.0603422998338 m^3 Massa: 36.2053799002 kg Coordinate del baricentro [m]: 1.86287365217e-09 1.73320615207e-09 -0.301522010319 Momenti d'inerzia centrali: Ix (beccheggio)= 13.6489940604 kg*m^2 Iy (rollio)= 13.6479107636 kg*m^2 Iz (imbardata)= 20.7960961313 kg*m^2 B - Grandezze relative allo scafo carico: Massa: 186.2053799 kg Volume immerso: 0.1862053799 m^3 Coordinate del baricentro [m]: 3.62213209517e-10 3.37000935283e-10 -0.0650717983465 Momenti d'inerzia centrali: Ix (beccheggio)= 16.1617684079 kg*m^2 Iy (rollio)= 15.681706587 kg*m^2 Iz (imbardata)= 20.7960961313 kg*m^2 Tabella di stabilità: angolo braccio[m] momento raddrizzante [N*m] piano di gall.[m](*) xC [m] yC [m] zC [m] 0.0° 1.49536251636e-08 2.73154099083e-05 -0.555480462886 1.53158383731e-08 3.20380786968e-08 -0.628136792354 3.0° 0.0113187140671 20.6756094925 -0.554889121447 0.0407862639545 3.83526730333e-08 -0.627049747729 6.0° 0.0234035178916 42.7506158215 -0.556411283379 0.0822432261061 4.281431951e-08 -0.623667696833 9.0° 0.0363184302058 66.3419603907 -0.558375786602 0.124383948277 4.78956550269e-08 -0.618237271728 12.0° 0.04946220043 90.3513539316 -0.561419498698 0.166502592015 5.00130448744e-08 -0.610504860166 15.0° 0.0652896778723 119.263007756 -0.565457306389 0.210866552753 2.36783829513e-06 -0.599776541298 18.0° 0.0771655149922 140.956299877 -0.571903749507 0.250837214437 -5.3929673745e-06 -0.587356510583 21.0° 0.084276293266 153.945379193 -0.581153581035 0.286005654623 6.81957289644e-06 -0.574975062997 (*)Per il significato di questa grandezza si veda la guida Altezza metacentrica: - Valutazione 1: § momento d'inerzia dell'area: 0.152136124171 m^4 § I / V immerso= r =0.817033988237 m § zG - zC = a =0.563064994007 m § GM = r-a =0.25396899423 m - Valutazione 2: § GM = b/sen(phi) =0.216270321203 m § GM = interp.(b/sen(phi))=0.200955778002 m Periodo dell'oscillazione trasversale: 18.6106085118s
Come spiegato nella sezione "funzionamento del programma" il documento relativo ai volumi componenti lo scafo contiene un'approssimazione dello scafo con il suo spessore adatta a svolgere il calcolo di stabilità, ma non una vera modellazione solida generata dalla semplice superficie "stl" acquisita; pertanto non è possibile esportare questi dati in formato stl o fbd, come si può fare per gli scafi prodotti internamente dal modellatore automatico di calcnav.
4 - FUNZIONAMENTO DEL PROGRAMMA:
Le note seguenti, dal momento che illustrano i procedimenti seguiti dal programma durante la modellazione superficiale e solida e durante il calcolo, richiedono qualche nozione di geometria analitica e di fisica; il programma è utilizzabile anche senza la comprensione precisa di questa sezione.
Tutti gli script sono scritti in python; ciascuno esegue una funzione specifica. Il programma (o, meglio, lo script) principale "calcnav-x.y.z" è l'unico che debba essere usato direttamente dall'utilizzatore: esso genera l'interfaccia grafica e si preoccupa di richiamare gli altri script a seconda delle richieste dell'utilizzatore, fornendo loro i valori impostati dei parametri. La seguente tabella elenca le funzioni di ogni script del pacchetto.
| NOME | FUNZIONE |
| calcnav | genera l'interfaccia grafica; legge i valori dei parametri impostati dall'utilizzatore; richiama gli altri script a seconda delle operazioni richieste fornendo i parametri necessari |
| superfici | è il modellatore automatico: salva i punti delle superfici interna ed esterna nei documenti "sup_scafo_est" e "sup_scafo_int" |
| scafocalc | legge i dati prodotti da "superfici"; prepara i dati per i calcoli di stabilità: divide lo spessore dello scafo in tetraedri e salva i dati in "datiscafovol", divide la superficie esterna dello scafo in triangoli e salva i dati in "datiscafosup" |
| scafocalc2 | legge i dati prodotti da scafocalc; calcola massa, baricentro, momento d'inerzia dello scafo vuoto e carico; esegue il calcolo di stabilità trascurando il beccheggio |
| scafocalc2plus | esegue le stesse operazioni di scafocalc2, ma tiene conto dell'inclinazione assunta in beccheggio durante il calcolo di stabilità |
| algvett | è una libreria di funzioni ed oggetti che facilitano le operazioni vettoriali eseguite dagli script |
| 2stl | produce la modellazione superficiale dello scafo nel formato stl a partire dai documenti prodotti da "superfici" |
| 2cgx | produce la modellazione solida dello scafo nel formato fbd a partire dai documenti prodotti da "superfici" |
| stl2calc | legge un documento stl rappresentante la superficie esterna di un galleggiante e ne ricava i dati necessari ad eseguire il calcolo di stabilità: produce "datiscafosup" e "datiscafovol", quest'ultimo approssimato |
| scafo3d.blend | è un documento di Blender che include lo script "scafo3d" (quest'ultimo scritto in python), il quale istruisce Blender ad eseguire la resa delle superfici a partire dai dati prodotti da "superfici" |
| pres2pres.py | script accessorio, esterno a Calcnav, che facilita l'attribuzione dei valori di pressione idrostatica sulla superficie esterna nella preparazione del calcolo strutturale |
| q0.py | legge un documento "datiscafosup" contenente la superficie esterna di uno scafo approssimata da elementi triangolari e restituisce un valore di prima approssimazione del piano di galleggiamento, da passare a "scafocalc2"; si usa in seguito all'importazione di un "stl" esterno |
4.2.1 - Definizione delle superfici
Ogni mezza sezione trasversale dello scafo (ordinata) viene resa con due archi di parabola passanti per il punto A (intersezione con la chiglia) e per B (intersezione con il bordo), raccordati fra loro in un punto intermedio. Le due parabole sono soggette ai seguenti vincoli:
I arco – passaggio per A
I arco – tangente in A di valore assegnato
II arco – passaggio per B
II arco – tangente in B di valore assegnato
I e II arco – passaggio per un punto intermedio
I e II arco – tangente comune nel punto di raccordo
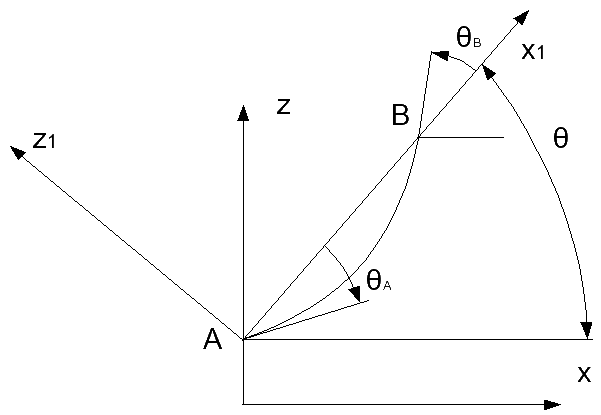
Prendendo un sistema di riferimento x1-z1 come in figura,
indicando con
y=a1x2+b1x+c1
y=a2x2+b2x+c2
le due parabole, i coefficienti si trovano in base al sistema

con
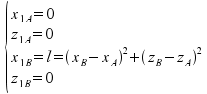
xr è il punto di raccordo fra i due archi, che può essere impostato in maniera automatica oppure manualmente; nel primo caso esso viene scelto dal programma, come indicato nelle figure, quale ascissa x1 in corrispondenza della quale i punti delle rette tangenti alla curva in A e in B hanno la stessa distanza dall'asse x1 stesso.
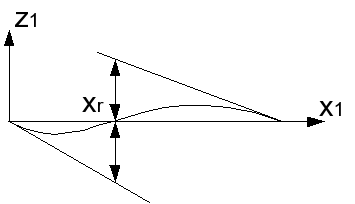
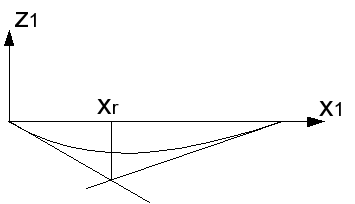
Nel secondo caso esso viene ricostruito per interpolazione parabolica in maniera
da rispettare i tre valori scelti manualmente in corrispondenza delle sezioni
di poppa, maestra e della base della ruota di prua.
Il programma vincola a scegliere un numero intero compreso fra 1 e 99: la risoluzione
ottenuta in questo modo appare più che accettabile, ed il campo risulta tale che la curva
ottenuta sia in ogni caso composta da due archi di parabole (ciò che evidentemente non
avverrebbe qualora il parametro valesse 0 o 100), così da soddisfare in ogni caso
le condizioni imposte su tangenza e punti di passaggio.
Gli archi vengono quindi ricostruiti per punti, dividendo il segmento da x1=0 a x1=l in n intervalli uguali (con n pari al numero di punti su ogni mezza sezione, impostato dall'utilizzatore), e calcolando la corrispondente z1. Naturalmente vale poi la relazione
che permette di risalire alle coordinate del punto.
I valori di zA, xB, zB e degli angoli in A e in B vengono fatti variare con opportune interpolazioni (in questo caso con polinomi di primo e secondo grado) fra i valori impostati nella schermata del programma dall'utilizzatore.
Curando di raccordare bene gli archi di curva (continuità della derivata prima) la superficie risulta liscia e ben modellata.
La ricerca della superficie interna dello scafo, necessaria a stabilirne la massa e la posizione del baricentro, si esegue tenendo conto che la superficie esterna si può scrivere in forma parametrica, in funzione di due parametri a e b, nel seguente modo:
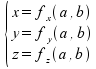
In questo caso a e b corrispondono alle coordinate indipendenti x1 e y, per cui l'espressione precedente si può riscrivere come
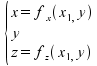
Pertanto è possibile trovare per ogni punto, definito dai parametri x1P e yP, due vettori tangenti alla superficie e indipendenti fra loro come
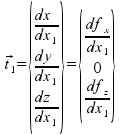
e

Si trova allora il versore normale alla superficie come
Pertanto, dato un punto P=(x,y,z) della superficie esterna, detto s lo spessore dello
scafo, il corrispondente punto della superficie interna è
Q=P+s n
4.2.2 - Distribuzione dei punti in zone particolari
In corrispondenza della chiglia, se lo scafo non è piatto, le sezioni presentano
una cuspide, che rende non più valido il sistema di calcolo del punto interno
corrispondente ad ogni punto esterno.
Lo script "superfici" in questo caso provvede a portare i punti della superficie
interna sul piano di mezzeria dello scafo, in modo da raccordare opportunamente
le due lastre che vi concorrono senza generare sovrapposizioni o vuoti e
mantenendo lo spessore richiesto.

L'immagine illustra la resa di una sezione affilata
Lo specchio di poppa viene chiuso da spicchi concorrenti nel punto di mezzeria del bordo superiore, rettilineo. La lunghezza media degli spicchi è pari a quella dei rettangoli che compongono la superficie esterna dello scafo (e dunque alla distanza fra due ordinate adiacenti). La lunghezza effettiva è attribuita secondo una progressione tale da ottenere superfici approssimativamente costanti per gli elementi costituenti lo specchio: considerando un segmento congiungente il centro dello specchio con uno dei punti lungo il bordo, assumendo un'ascissa "x" lungo di esso e lo zero nel centro dello specchio, chiamando "l" la lunghezza del segmento ed "n" il numero di porzioni in cui il segmento stesso deve restare suddiviso, l'ascissa del punto di divisione i-esimo si trova come

Gli elenchi dei punti delle due superfici vengono salvati nei due documenti “sup_scafo_est” e “sup_scafo_int”.
4.3.1 - Operazioni effettuate in seguito alla modellazione automatica
Considerando due punti adiacenti lungo una mezza sezione della superficie esterna, i due punti corrispondenti lungo la sezione successiva e i quattro punti omologhi sulle due sezioni adiacenti corrispondenti sulla superficie interna, si individua una porzione di solido (una “lastra” approssimativamente rettangolare) che approssima una parte dello scafo: nella figura, il tratto compreso fra i punti A,B,C,D,E,F,G,H segnati.

Tale solido, come illustrato nelle figure, può essere diviso in due prismi irregolari a base triangolare, ciascuno dei quali viene diviso in tre tetraedri (irregolari). Scegliendo opportunamente i piani di divisione fra i tetraedri è possibile fare in modo che tra un prisma e quelli adiacenti non rimangano vuoti.
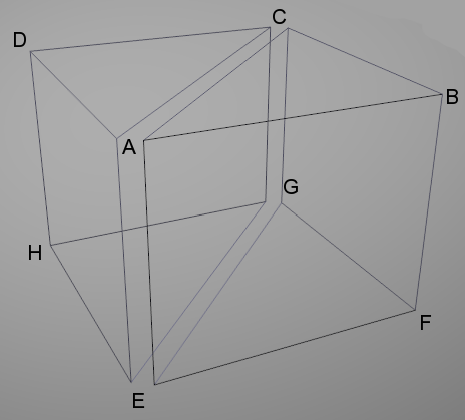
Con riferimento alla figura i due prismi ACDEGH e ABCEFG vengono divisi
rispettivamente nei tetraedri:
ACDH, EGHC, ACEH;
ABCE, EFGB, BCEG.
Nella zona prodiera le sezioni vengono approssimate con un numero di punti
decrescente verso l'estrema prua (rappresentata da un punto solo):
ciò dà luogo a gruppi di facce triangolari, a cui
corrispondono prismi non accoppiati. Essi vengono divisi come il
prisma ACDEGH testè menzionato.
La tetraedralizzazione così introdotta funziona anche nel caso di prismi degeneri in cui una base sia sostituita da un segmento o da un punto, cosa che avviene se due o più punti coincidono (come può accadere nelle zone adiacenti alla chiglia): essa risulta pertanto particolarmente efficace per il calcolo del volume proprio dello scafo (e dunque
della sua massa) nonché del centro di gravità. Infatti,
indicando con A, B, C, D i vettori che individuano i vertici di un
generico tetraedro, il suo baricentro si può scrivere come
G=(A+B+C+D)/4
dove la somma è la consueta somma vettoriale.
Il volume invece è dato dal prodotto misto fra i vettori corrispondenti a tre lati del
tetraedro che siano congiunti dallo stesso vertice: vale cioè
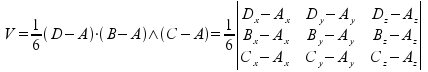
Pertanto il programma provvede a leggere i documenti contenenti gli elenchi di punti relativi alle superfici esterna ed interna, a rilasciare un ulteriore documento contenente l'elenco dei vertici dei tetraedri in cui rimane suddiviso lo scafo, quindi a calcolare la somma dei volumi dei tetraedri ed il baricentro comune secondo la consueta formula

Il volume complessivo viene poi ricalcolato per approssimazione come prodotto fra l'area della superficie esterna dello scafo per lo spessore: tale operazione, molto più banale, dà regolarmente un valore leggermente superiore alla somma dei volumi dei tetraedri: tale sovrastima è ovviamente dovuta al fatto che con quest'ultimo sistema i prismi componenti lo scafo vengono considerati retti, mentre la base giacente sulla superficie interna è di norma inferiore a quella esterna. Meno è accentuata la curvatura dello scafo e meno l'effetto risulta importante, mentre la vicinanza fra i due risultati conferma la bontà del calcolo.
Il programma funziona, per scelta progettuale, utilizzando gli elenchi di
coordinate salvati su disco fisso, in modo da non richiedere grandi quantità di memoria
allocata; ciò naturalmente aumenta i tempi di calcolo, ma consente di far funzionare
calcnav su calcolatori di capacità ridotte anche spingendo ad un grado molto elevato
la definizione dello scafo: normalmente piccoli calcolatori casalinghi possono eseguire
l'intero calcolo approssimando lo scafo con vari milioni di punti, a patto che vi sia
abbastanza spazio sul disco fisso per salvare i documenti provvisori (nella cartella "temp",
che di norma, operando con un numero di punti dell'ordine delle migliaia raggiunge
dimensioni di qualche megabyte).
Naturalmente non è detto che, una volta ottenuta una modellazione composta da milioni di punti
ed eseguiti i calcoli con calcnav, sia possibile usarla per visualizzare il risultato con Blender
o con altri programmi di disegno. In questo caso si possono produrre documenti diversi,
caratterizzati da un minor numero di punti, per la resa grafica.
4.3.1 - Operazioni effettuate in seguito all'importazione di una superficie "stl" prodotta esternamente
L'importazione di una superficie galleggiante ottenuta attraverso un programma esterno rende molto più flessibile
il programma e più interessante il suo uso, tanto più che è possibile modificare uno scafo ottenuto con calcnav stesso
(aggiunta di coperta, modifiche all'opera viva, introduzione di più scafi, ecc.). Naturalmente in questo caso risulta
molto più complesso ricavare una corretta modellazione solida del volume proprio dello scafo, dal momento che non
si dispone più delle curve analitiche da cui sono stati dedotti i punti approssimanti la superficie, ma solamente i
punti stessi, senza più alcuna indicazione, ad esempio, sul fatto che il diedro definito da due superfici
triangolari rappresenti effettivamente un diedro (cioè lo scafo presenti un qualche spigolo) o approssimi una
superficie curva.
Si è optato quindi per una soluzione approssimata, che fornisca risultati sufficientemente corretti senza introdurre
algoritmi di modellazione troppo sofisticati, la cui validità peraltro risulterebbe comunque sminuita dall'impossibilità
di ricostruire tutte le strutture fisse interne allo scafo (bagli, correnti, ordinate, ecc.), la cui presenza può essere
simulata solo da una modellazione totale che ne tenga conto (si spera che prossime versioni del programma siano in grado
di acquisire anche questo tipo informazioni).
Il programma che gestisce l'importazione dal formato stl, pertanto, genera per ogni triangolo della superficie un prisma
retto avente per base il triangolo stesso e per altezza lo spessore della scafo. La seconda base del prisma corrisponde alla
superficie interna dello scafo; ciò si ottiene sommando ad ogni vertice del triangolo di partenza un vettore avente modulo
pari allo spessore dello scafo, direzione parallela alla normale uscente dichiarata nell'stl e verso opposto.
È evidente che i vertici delle basi interne di prismi adiacenti non coincidono, per cui i prismi stessi risultano
parzialmente sovrapposti dove lo scafo è concavo, mentre si allontanano dove lo scafo è convesso. Complessivamente deriva
una sovrastima del volume e della massa propria dello scafo che mediamente è contenuta sotto lo 0,5%.
Ogni prisma viene diviso in tre tetraedri esattamente come illustrato nel paragrafo precedente: in questo modo si compone
un documento con i dati dei volumi che viene passato allo script di calcolo, il quale esegue le stesse operazioni viste
per ricavare volume proprio, massa e baricentro. Anche i momenti d'inerzia si ricavano dai tetraedri così prodotti, e
risultano dunque affetti da una leggera sovrastima.
4.4.1 - Sbandamento sull'asse di rollio (inclinazione in beccheggio vincolata)
Durante la fase di tetraedralizzazione del volume proprio dello scafo il programma
genera un ulteriore documento che contiene informazioni sui triangoli
che compongono la superficie esterna, e serve ad effettuare il calcolo
di stabilità. Tale documento viene prodotto in maniera del tutto analoga sia a partire
dalla modellazione automatica, sia a partire da una superficie prodotta esternamente ed importata
come "stl", per cui le spiegazioni seguenti sono valide in entrambi i casi.
Conoscendo la massa totale dello scafo (massa propria e masse aggiuntive), il
volume immerso è naturalmente pari a
Vimm=massa/densità dell'acqua
Per ogni angolo di sbandamento imposto allo scafo il programma esegue allora la ricerca
della posizione del piano di galleggiamento, definito come il piano inclinato
dell'angolo richiesto e tale da tagliare sullo scafo un volume pari a
quello immerso richiesto. Per ovvie ragioni di comodità e rapidità di
calcolo si assume il sistema di riferimento fisso rispetto all'oggetto più complesso
da descrivere, cioè lo scafo, e si fa muovere il più semplice, cioè
il piano, anche se nella realtà la superficie marina rimane ferma e lo scafo si sbanda!
Naturalmente occorre adattare la coppia raddrizzante, come verrà esposto poco oltre,
tenendo conto che le forze agiscono sempre perpendicolarmente alla superficie marina.
Rispetto agli assi x, y, z, fissi rispetto
allo scafo e presi come inizialmente descritto, il piano si scrive:
z = x tang(φ) + q
dove φ è l'angolo imposto.
Pertanto viene assunto un valore di primo tentativo di q, e con esso si valuta il
volume immerso: il programma scorre l'elenco dei triangoli componenti
la superficie esterna; quando il baricentro del triangolo risulta
sotto il piano di galleggiamento, il triangolo stesso fa parte della
superficie immersa. Perciò, se il vettore normale uscente dallo scafo è
rivolto verso il basso, la porzione di volume compresa fra il triangolo stesso e il piano
di galleggiamento è vuota e contribuisce al galleggiamento; in caso contrario la
porzione è piena d'acqua e non contribuisce al galleggiamento, come viene
schematizzato nella figura (bidimensionale per chiarezza): il caso a) è quello di un
normale scafo convesso in cui tutte le porzioni dello stesso chiudono il volume vuoto; nel
caso b) lo scafo presenta una concavità e il volume complessivo è dato dalla somma
delle porzioni vuote meno la somma di quelle piene.

Nel caso tridimensionale valutato dal programma la porzione di volume soprastante
ogni triangolo è un prisma ottenuto proiettando il triangolo stesso sul piano
di galleggiamento secondo la direzione z (verticale): se A è un vertice del triangolo, la sua proiezione
sul piano di galleggiamento è un punto D tale che:
Dx=Ax
Dy=Ay
Dz=Axtang(φ)+q
In questo modo il triangolo ABC e la sua proiezione DEF costituiscono
le basi di un prisma avente facce laterali piane (cioè i quattro
vertici di ogni faccia sono complanari). L'insieme di questi prismi discretizza il volume immerso
complessivo. Dividendo ogni prisma in tetraedri, come già
illustrato per il volume proprio dello scafo, si risale al valore del
volume immerso (effettivo); in questo caso la caratteristica dei prismi di avere
facce laterali piane permette di assumere una divisione di ogni prisma in tetraedri indipendente dalla divisione dei prismi adiacenti, pur con la certezza di non lasciare vuoti fra un prisma e l'altro. In pratica il prisma ABC-DEF (dove i punti D, E, F sono le proiezioni rispettivamente
di A, B, C) viene diviso nei tre tetraedri: A,B,C,F; D,E,F,A; A,B,E,F.
Sommando il volume dei tetraedri vuoti e sottraendo quello degli eventuali pieni si ottiene dunque il volume immerso effettivo dell'iterazione: esso viene confrontato con il volume immerso richiesto e, in base alla differenza fra i due, si corregge il parametro q
sommandogli la variazione:
Δq = (Volrichiesto-Voleffettivo)/Area di galleggiamento;
si tratta, in pratica, dell'altezza media (con segno) di un solido avente per volume la
differenza di volumi da colmare e per area di base l'area della superficie tagliata dal
piano di galleggiamento sullo scafo durante l'iterazione in corso.
Il procedimento converge piuttosto rapidamente e dopo
alcune iterazioni risale alla posizione corretta del piano di
galleggiamento. Ciò avviene, naturalmente, a patto che l'approssimazione
richiesta sul volume immerso non sia troppo piccola rispettto alle dimensioni dei triangoli
costitutenti lo scafo; in questo caso può non esistere un valore di q per cui la differenza
fra volume richiesto e volume effettivo sia abbastanza piccola, e dunque l'algoritmo non
è in grado di convergere.
Risulta evidentemente comodo che il programma stesso dia avviso di questa circostanza, ma
per far ciò occorre rilevare l'eventuale ripetizione, nel corso delle iterazioni,
di un valore del volume o della posizione "q" del piano di galleggiamento; purtroppo ciò
comporta l'allocazione di quantità di memoria abbastanza grandi per uno scopo di
importanza relativa nell'economia del funzionamento (soprattutto rispetto alla sobrietà
nell'uso di memoria che si è cercato di attribuire a calcnav, come già
spiegato), nonché tempi di elaborazione via via crescenti con il numero delle iterazioni. Si
è preferito quindi tralasciare questa possibilità limitandosi ad inserire un controllo
sulla grandezza del valore di "Δ q": qualora esso aumenti in valore assoluto fra due iterazioni
successive, il programma avvisa della possibilità che sia verificato l'ingresso in un ciclo
senza uscita, senza bloccare l'esecuzione. È perciò cura dell'utilizzatore verificare
che il calcolo si svolga regolarmente.
Una volta che si è trovata la posizione del piano di galleggiamento la suddivisione in prismi ed in
tetraedri viene ripetuta, tenendo conto del baricentro dei tetraedri,
dal quale si risale al baricentro del volume immerso.
Dato questo funzionamento si capisce come, qualora il bordo della superficie esterna si trovi sotto il pelo dell'acqua, venga inclusa nel volume immerso una porzione di volume che non dovrebbe far parte dello scafo in quanto si trova al di sopra della coperta. In questo caso, ovviamente, il volume immerso viene sovrastimato ed il suo baricentro si trova più lontano dal piano di mezzeria rispetto al vero: la coppia raddrizzante calcolata non è corretta e molto probabilmente viene sovrastimata. Il difetto del programma, che comunque si verifica per angoli molto elevati, potrebbe essere corretto modellando almeno la superficie esterna della coperta, anche se rimarrebbe il problema di quali porzioni di tale coperta considerare ermetiche, e ancora non si terrebbe conto di altri volumi, a cominciare da cabine sporgenti: questo è un tipico caso in cui la modellazione automatica va quantomeno integrata da interventi manuali; come già illustrato è possibile usare calcnav per svolgere la simulazione anche su un disegno eseguito o adattato esternamente.
Conoscendo la posizione del centro di gravità della nave e del baricentro
del volume immerso, si risale molto semplicemente al momento
raddrizzante: vale infatti
My=9,81 mtot b
dove, chiamando G il centro di gravità della nave e C il baricentro del volume
immerso, il braccio raddrizzante b si scrive
b = (xC-xG) cos(φ) + (zC-zG) sen(φ)
cioè proiettando la distanza fra G e C sulla retta giacente nel piano di galleggiamento e
ortogonale all'asse dello scafo.
Il calcolo del braccio e del conseguente momento raddrizzante viene ripetuto tante volte quante sono richieste impostando per ciascuna l'inclinazione relativa. In questo modo, alla fine del ciclo viene restituita la tabella che fornisce per ogni angolo il braccio, il momento, la posizione del piano di galleggiamento, le coordinate del baricentro.
Infine il programma calcola l'altezza metacentrica "GM". Si ricorda che il metacentro è
il punto d'intersezione fra la retta ortogonale al piano di galleggiamento passante per il centro di spinta e
l'asse verticale del galleggiante passante per il baricentro; in pratica l'intersezione fra la retta verticale
per il centro di spinta e l'asse per il baricentro che risulta verticale a nave non inclinata.
Per una nave non inclinata ed equilibrata le due rette coincidono, per cui il metacentro si individua
come limite di tale intersezione.
Come si può facilmente verificare con un disegno la distanza "GM" fra baricentro e metacentro
è pari al braccio raddrizzante diviso per il seno dell'angolo di inclinazione. Ciò fornisce un
primo sistema per eseguirne il calcolo: infatti, da quanto esposto, vale
GM = lim (φ -> 0) (b/sen(φ))
e dunque GM si può trovare come derivata del braccio rispetto all'angolo. Per approssimare
questo valore il programma pertanto esegue il rapporto fra il braccio relativo al primo angolo valutato
dopo gli 0° ed il seno dell'angolo stesso; quindi una migliore approssimazione si ottiene estrapolando il valore
del rapporto fra braccio e seno dell'angolo per i primi due valori oltre gli 0°. Ad esempio, si supponga che sia stato richiesto
il calcolo dei bracci ad intervalli di 3°. Se lo scafo è equilibrato, a 0° si trova un braccio praticamente nullo;
perciò un valore di prima approssimazione dell'altezza metacentrica è dato dal braccio a 3° diviso per
il seno di 3°. Ma un'approssimazione migliore si ottiene considerando anche il braccio a 6° diviso per il seno di 6°,
ed estrapolando linearmente il valore di braccio/seno a 0°.
Vengono così rilasciati entrambi i valori, in genere abbastanza vicini, purché gli intervalli angolari richiesti
siano di pochi gradi (naturalmente, più ampi sono gli intervalli, meno l'estrapolazione ha significato).
È poi interessante verificare la corrispondenza fra questi valori dell'altezza metacentrica e
quello trovato secondo una "classica" formula, in base alla quale
GM = I/Vimm - (zG-zC).
Qui "I" è il momento d'inerzia centrale dell'area di sezione della nave al piano di galleggiamento
(ovviamento rispetto all'asse di rollio); Vimm è il volume immerso; (zG-zC) rappresenta
la distanza in verticale del centro di gravità dal centro di spinta; tutte le grandezze si considerano
per uno sbadamento nullo.
Il programma dispone già del volume immerso e anche della differenza zG-zC. Esegue quindi il calcolo del
momento d'inerzia dell'area al piano di galleggiamento per 0°, usando la proiezione sul piano stesso dei triangoli
nei quali lo scafo è suddiviso. Il calcolo avviene secondo la formula:
I = Σi(Areai xi2),
dunque trascurando il momento d'inerzia proprio dei triangolini; viene contestualmente calcolato il baricentro della
superficie in modo da trovare il momento d'inerzia centrale con il teorema di Huygens-Steiner, anche per eventuali scafi non simmetrici.
I tre valori dell'altezza metacentrica rilasciati in questo modo in genere differiscono di pochissimi centimetri; naturalmente
approssimazioni eccessive nei dati di partenza possono falsare il risultato.
4.4.2 - Inclinazione sull'asse di beccheggio libera
Nel caso che venga richiesta la valutazione dell'assetto in beccheggio, il
programma esegue la ricerca del piano di galleggiamento in maniera del tutto analoga
a quella testè illustrata, solo introducendo un ulteriore parametro per la
definizione del piano; esso ora si scrive come:
z = x tang(φ) + y tang(θ) + q.
Come prima, lo sbandamento in rollio "φ" viene imposto, mentre q e lo
sbandamento in beccheggio "θ" vengono ricercati per iterazioni.
La correzione apportata a q ad ogni iterazione è già stata illustrata; la
correzione apportata a θ si basa sulla valutazione del braccio del
momento di beccheggio, dato dalla distanza fra centro di gravità della
nave e baricentro del volume immerso proiettata sulla retta risultante
dall'intersezione fra il piano di mezzeria dello scafo e il piano di galleggiamento.
Tale braccio si scrive:
bbeccheggio=(yC-yG) cos(θ) + (zC - zG) sen(θ)
l'inclinazione in beccheggio viene allora adeguata sommando all'angolo θ, ad ogni iterazione, la quantità:
Δθ = - K × bbeccheggio / Lunghezza scafo
dove K è un valore costante assunto in base all'esperienza, in maniera che la variazione
di θ non sia troppo grande da divergere, né troppo piccola da convergere con
eccessiva lentezza.
4.4.3 - Momenti d'inerzia e periodo delle piccole oscillazioni
Durante il calcolo il programma risale inoltre ai momenti d'inerzia centrali del solo scafo e della nave (scafo più masse aggiuntive); essi inizialmente vengono calcolati come

dove le somme vengono eseguite sui tetraedri componenti il volume proprio dello scafo. Non si tiene conto in questo modo dei momenti d'inerzia centrali dei tetraedri, per cui il calcolo è tanto più preciso quanto più fine è la discretizzazione dello scafo.
Una volta trovata la posizione del centro di gravità G=(xG,yG,zG), i momenti, inizialmente scritti rispetto all'origine degli assi, vengono riferiti al centro di gravità nel modo seguente
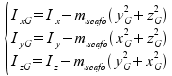
Analogamente si trovano i momenti centrali della nave carica, anch'essi riferiti al
nuovo centro di gravità.
Infine viene calcolato il periodo di oscillazione sull'asse di beccheggio secondo
la formula semplificata:
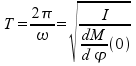
Ricordando che la nave oscilla intorno ad un asse d'istantanea rotazione
costituito da una retta giacente sul piano di galleggiamento e passante per
il baricentro dell'area intersecata su tale piano dallo scafo, il momento
d'inerzia usato in questo caso è quello rispetto alla retta
data dall'intersezione del piano y-z con quello di galleggiamento a
nave non inclinata, e si scrive
I=Iy + mnave [xG2 + (zG - q)2]
dove Iy è il momento d'inerzia centrale, xG
e zG le coordinate del baricentro, q la posizione sull'asse z del piano di
galleggiamento in corrispondenza dello sbandamento nullo.
La derivata del momento nell'origine, invece, viene sostituita dal rapporto
incrementale tra momenti e angoli per i primi due valori calcolati
nel diagramma.
Tenendo conto dei dati risultanti dal calcolo di stabilità già effettuato, sarebbe piuttosto semplice ricostruire in via approssimata il periodo di oscillazione per grandi angoli.
Si tratta della superficie dello scafo, racchiudente il suo volume proprio,
approssimata da triangoli, per ciascuno dei quali vengono forniti i vertici ed il versore
normale. Blender, come molti altri programmi, legge il formato stl.
Per ottenere il documento "scafo.stl" è sufficiente premere il pulsante
"esporta dati"; dalla finestrella che si apre scegliere il pulsante "genera stl".
Si ricordi che la modellazione viene eseguita a partire dai documenti già prodotti
da calcnav e salvati sul disco fisso: per ottenere nel documento stl qualunque modifica apportata
è necessario prima premere il pulsante "solo disegno" per generare le superfici.
Anche il documento "scafo.stl", come quelli delle superfici, viene salvato nella cartella stessa di calcnav,
ma copiato subito dopo in quella di Blender, in modo da consentirne immediatamente l'acquisizione
senza dover eseguire "manualmente" la copia. L'impostazione è la stessa adoperata per la
copia delle superfici, e si trova in "impostazioni.py".
Infine pare opportuno precisare che non è possibile esportare
in formato stl una modellazione importata da programmi esterni in calcnav attraverso il
formato stl: in questo caso, infatti, calcnav produce (come già spiegato) una superficie
interna approssimata, costituita da triangoli scollegati fra loro, e dunque l'stl in uscita da
calcnav non risulterebbe una superficie chiusa racchiudente un volume finito.

Immagine di uno scafo esportato come stl ed acquisito in Blender.

Dettaglio della prua dello stesso scafo: si osservi lo spessore del bordo.
Il secondo formato richiede alcune spiegazioni accurate, in quanto esso rappresenta
la modellazione solida dello scafo, direttamente adoperabile nel programma di calcolo
strutturale agli elementi finiti "Calculix". Tale programma è liberamente scaricabile
per ambienti unix da
www.calculix.de
mentre per altri sistemi operativi è possibile trovare in rete il programma compilato.
Le presenti spiegazioni illustrano solo il modo di importare in Calculix i dati in uscita da Calcnav, e non pretendono minimamente di servire alla comprensione del metodo di calcolo strutturale agli elementi finiti.
Perciò occorre scaricare e installare Calculix, che è costituito da due programmi: cgx,
il pre- e post-processore, e ccx, il solutore. Calculix viene fornito
completo di spiegazioni e con un ricco repertorio di esempi.
Nonostante ccx sia in grado di effettuare calcoli su elementi di
molti tipi diversi, il preprocessore può meshare oggetti tridimensionali solo in elementi
del tipo esaedro (prismi irregolari a base quadrangolare), ad 8 o a 20 nodi, e solo a partire
da geometrie piuttosto semplici (prismi con facce di base aventi da tre a cinque lati).
Perciò, volendo usare cgx come preprocessore, oggetti dalla geometria più complessa devono
essere preliminarmente suddivisi in solidi semplici. Ciò costituisce naturalmente una
complicazione nella fase di modellazione, anche se il risultato è una mesh strutturata
molto precisa.
Calcnav esporta lo scafo già suddiviso in prismi a base rettangolare o triangolare e pronto
per essere meshato senza difficoltà, o per essere completato usando gli strumenti del
cgx. Si è scelto di esportare il volume dello scafo in questo modo anziché già meshato in
tetraedri (come sarebbe stato più naturale, dal momento che calcnav esegue già la tetraedralizzazione
per il calcolo di stabilità): così infatti è possibile usare cgx per introdurre nuovi elementi
che abbiano importanza dal punto di vista strutturale.
D'altra parte gli elementi cubici a 20 nodi forniscono un ottimo risultato, nonostante non abbiano la
flessibilità geometrica dei più consueti tetraedri.
Disponendo di preprocessori più potenti, in grado di meshare in tetraedri
(ad esempio, fra quelli di libero utilizzo, gmsh),
sarà invece possibile usare il documento stl fornito da Calcnav.
Per seguire le indicazioni di questo capitolo, dunque, si scarichi ed installi Calculix (non disponete di un sistema operativo Unix/Linux? Magari questa è l'occasione per provarlo!)
Il documento scafo.fbd esportato da Calcnav contiene la sequenza di istruzioni per far eseguire
al preprocessore cgx la modellazione solida: ne risulta lo scafo diviso in prismi a base rettangolare
o triangolare (gli stessi prismi illustrati nel paragrafo "Calcolo del volume proprio e del baricentro
dello scafo"). Ciascuno di essi verrà suddiviso in elementi al momento della meshatura. Dalla finestra
di esportazione di Calcnav è possibile scegliere quale dei due tipi di elementi disponibili in cgx
adoperare:
- he8: esaedri a otto nodi, cioè elementi a forma di cubi irregolari con un nodo ad ogni vertice;
- he20: esaedri a venti nodi, elementi a forma di cubi irregolari con un nodo ad ogni vertice e un nodo
a metà di ogni spigolo;
tale impostazione verrà tradotta nel comando "elty all he8" oppure "elty all he20", salvato alla fine
del documento fbd.
Il numero di elementi in cui ogni prisma viene suddiviso dipende dal parametro "ld", che stabilisce
in quanti segmenti debba essere suddiviso ogni spigolo del prisma: ogni segmento è individuato da due
nodi contigui. Ogni lato di un elemento he8 consta di un solo segmento (nodi nei soli vertici), mentre
ogni lato di un elemento he20 consta di due segmenti (nodi anche al centro dei lati). Perciò, se si impiegano
elementi he20, occorrerà impostare valori pari (multipli di due) per i parametri ld, altrimenti cgx
non sarà in grado di effettuare la meshatura.
Calcnav consente di impostare valori di ld diversi per i diversi tipi di linee costituenti gli spigoli
dei prismi: la finestrella di esportazione distingue fra tre tipi di linee:
- LO: linee orizzontali, incluse nella superficie dello scafo (collegano punti omologhi di due sezioni adiacenti);
- LV: linee verticali, incluse nella superficie dello scafo (collegano punti adiacenti della stessa sezione);
- LIE: linee interno-esterno, collegano la superficie esterna a quella interna attraversando il volume
proprio dello scafo (collegano il punto esterno ed il suo omologo interno della stessa sezione).
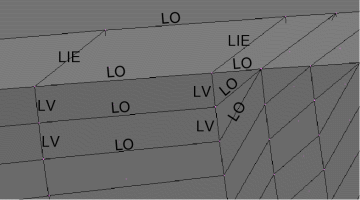
Naturalmente non è molto sensato infittire la griglia a partire da prismi di grandi dimensioni, poiché
la prima discretizzazione sulla geometria dello scafo viene introdotta da Calcnav e un successivo infittimento
degli elementi in cui i prismi vengono suddivisi non migliora l'approssimazione della geometria effettiva;
pertanto è logico aspettarsi che l'utilizzatore, se lo desidera, stabilisca un numero elevato di punti di approssimazione dello scafo (cioè infittisca i prismi in partenza), ma mantenga bassi i valori di ld. Al
più può essere interessante alzare il valore di ld per le linee interno-esterno LIE, in quanto ciò
aumenta il numero di "strati" di elementi lungo lo spessore dello scafo.
Una volta stabilite queste opzioni, premendo il pulsante "genera fbd", viene chiamato lo script "2cgx"
che scrive il documento "scafo.fbd".
Tale script adegua i punti della superficie interna in corrispondenza della chiglia, in modo da
conservare la forma corretta, senza vuoti né sovrapposizioni, ma anche eliminando i punti doppi,
così che i due mezzi scafi siano vincolati fra loro; inoltre i prismi generati hanno sempre basi
con tre o quattro lati e facce laterali con quattro.

Una sezione affilata vista nel cgx.
Attenzione: il documento "scafo.fbd" può diventare facilmente molto ingombrante, e non è detto che un
normale calcolatore casalingo sia poi in grado di gestirne il calcolo strutturale; ciò anche se lo
stesso calcolatore è in grado di far funzionare Calcnav sullo stesso scafo con la stessa
approssimazione! (Questo accade per la diversa gestione della memoria da parte dei due programmi,
come già precisato in precedenza).
Perciò, se si vuole comunque divertirsi ad usare il programma con un calcolatore di modesta
potenza, si abbassi la definizione della geometria, impostando un numero di punti basso in
Calcnav (pochi prismi), valori bassi per i parametri ld (pochi elementi per ogni prisma),
elementi he8 anziché he20.
Naturalmente il calcolo strutturale richiede l'imposizione dei carichi agenti: nel caso di una nave si tratta di valori di pressione distribuita e variabile lungo lo scafo, che non è agevole scrivere. A questo scopo, e limitatamente al caso di pressione idrostatica, con il pacchetto Calcnav viene fornito lo script "pres2pres" che rende abbastanza rapida questa operazione, sfruttando un "trucco" descritto nel seguito. La versione attuale funziona solo con elementi del tipo he8. Lo script non è integrato in Calcnav in quanto va utilizzato dopo il preprocessore cgx, e va dunque richiamato da console al momento opportuno. Poiché Calculix è disponibile solo per piattaforme unix si può immaginare che l'utilizzatore sia in grado di lanciare uno script da console senza troppi traumi! :-)
Per i passi successivi è molto opportuno leggere il manuale di Calculix.
Le indicazioni fornite qui servono come appunti sommari:
Trasferire "scafo.fbd" in una cartella appositamente creata.
Aprire una console ed entrare nella cartella ($ cd [nome cartella]).
Aprire "scafo.fbd" con cgx ("-b" significa che il programma viene usato come preprocessore):
$ cgx -b scafo.fbd
si apre la schermata del programma che contiene una colonna bianca a sinistra ed un riquadro a destra,
a sua volta contenente il disegno dello scafo. Usando il mouse si cambia il punto di vista dello scafo:
pulsante sinistro: cambia l'angolazione;
pulsante centrale: l'immagine viene zoomata;
pulsante destro: l'immagine viene traslata.
Quando si dà un qualunque comando da tastiera la
freccia del mouse va lasciata all'interno del riquadro di destra. Così, dopo aver
portato la freccia nel riquadro contenente il disegno dello scafo, lasciare il mouse e digitare da tastiera
i seguenti comandi per vedere gli oggetti di cui lo scafo stesso è composto:
plot p all [Invio] (si vedono solo i punti dello scafo)
plus l all [Invio] (si aggiungono le linee che collegano i punti)
plus ld all [Invio] (in corrispondenza di ogni linea compare il parametro ld impostato attraverso Calcnav)
minus ld all [Invio] (si nascondono i valori di ld)
plus s all [Invio] (si vedono le superfici appoggiate sui percorsi di linee chiusi)
plus b all [Invio] (si vedono i corpi compresi fra le superfici)
I comandi precedenti sono stati dati solo a titolo d'esempio e possono essere saltati durante l'uso normale; è invece indispensabile eseguire la meshatura, che permette di definire i nodi e gli elementi, cioè le entità adoperate durante il calcolo. Perciò, sempre lasciando la freccia del mouse nel riquadro,
mesh all [Invio] (esegue la meshatura)
Se si vogliono aggiungere elementi che avranno importanza dal punto di vista strutturale (ponte, bagli, ordinate),
sarà possibile farlo in seguito, e collegare la nuova modellazione
alla mesh già presente (si veda il manuale di cgx alla voce "mesh"), ma anche aggiungere
elementi alla modellazione direttamente a partire da "scafo.fbd".
In questo esempio si prosegue senza aggiungere elementi strutturali allo scafo (che risulta sicuramente
debole, ma questo, si ripete, è solo un esempio di base e non una simulazione per progettare una vera
nave!). Sempre per semplicità si assume che i carichi a cui lo scafo è soggetto (gli stessi che, si
ricorda, insieme al suo peso proprio, determinano la posizione del piano di galleggiamento definita
da q e phi) siano applicati al bordo superiore, come se lo scafo fosse chiuso da una coperta
su cui i carichi sono appoggiati: il bordo perciò viene considerato la porzione attraverso
cui lo scafo scarica le sollecitazioni risultanti dalla pressione e dal suo peso proprio, e viene
dunque vincolato.
Per definire gruppi di entità (nodi, punti, linee, superfici, corpi, elementi) da usare per applicare
vincoli o carichi o comunque da trattare in comune, Calculix definisce dei "set" (si leggano in proposito
le voci "seta" e "qadd" del manuale di cgx). In questo caso si selezionano tutti i nodi costituenti
il bordo superiore dello scafo e si salvano nel set "bordo":
(sempre lasciando la freccia del mouse nel riquadro del disegno)
plot n all [Invio] (si vedono solo i nodi colorati in rosso)
qadd bordo [Invio] (prepara il set bordo e si dispone ad includervi entità)
a (includerà nel set tutte le entità che verranno selezionate)
ora si definisce un rettangolo che si muoverà insieme alla freccia del mouse e servirà per selezionare tutti i nodi che cadono al suo interno: il rettangolo va immaginato sulla finestra del disegno, delle dimensioni che interessano, quindi si porta la freccia del mouse al vertice in alto a sinistra e si preme "r", poi al vertice in basso a destra e si preme ancora "r". Il rettangolo diventa visibile e accompagna la freccia del mouse.
Si gira lo scafo nel senso più opportuno; può andar bene scegliere dal menu di cgx (freccia del mouse nella finestra di cgx, colonna sinistra, cioè fuori del riquadro contenente il disegno, pulsante sinistro del mouse): orientation -> +y, lo scafo si vede da prua. Si ingrandisce (pulsante centrale del mouse) e si trasla (pulsante destro) fino a che si possono selezionare comodamente i soli nodi del bordo superiore.
Si inquadra un gruppo di tali nodi nel rettangolo e si preme "n" da tastiera;
quest'ultima operazione va ripetuta, eventualmente traslando lo scafo, fino a che tutti i nodi del bordo
superiore sono stati selezionati. Non ha importanza se alcuni nodi vengono selezionati più volte,
piuttosto si eviti di lasciarne fuori alcuni o di includerne altri che non c'entrino.
Alla fine premere "q" da tastiera per uscire dalla modalità di selezione.
Il documento scafo.fbd contiene un altro "set", già definito automaticamente da Calcnav, e rappresentante la superficie esterna: esso si chiama "supest" e va adoperato per imporre la pressione idrostatica come viene chiarito nel seguito
Ora, sempre lasciando ferma la freccia del mouse nel riquadro del disegno, si danno da tastiera i comandi necessari ad esportare i diversi documenti da assemblare per effettuare il calcolo con ccx (Si veda a questo proposito la voce "send" del manuale di cgx):
send all abq [Invio](salva la mesh nel file all.msh)
send bordo abq names [Invio](salva il set bordo nel file bordo.nam)
send bordo abq spc 123 [Invio](salva il vincolo sui gradi di libertà 1, 2 e 3 (traslazioni) per i nodi del set "bordo": genera "bordo.spc")
send supest abq pres 1 [Invio](impone un valore di pressione, scelto arbitrariamente, sulla superficie esterna: genera "supest.pres")
L'ultimo comando ha generato un file che definisce un carico di pressione imposta sulla superficie esterna dello
scafo, ma uniforme e pari ad un valore arbitrario (1 nell'esempio). A questo punto, adoperando lo script
pres2pres.py presente nel pacchetto, è possibile ottenere un nuovo documento contenente i corretti valori
di pressione da attribuire alla porzione immersa di superficie esterna (l'"opera viva"). Perciò si chiuda pure cgx,
si copi pres2pres.py nella cartella contenente i documenti prodotti da cgx (devono essere presenti il file della mesh "all.msh" e quello
della pressione fittizia "supest.pres"); si ricordi di attribuirgli eventualmente il permesso di esecuzione (chmod a+x pres2pres.py).
Ora si lancia lo script
$ pres2pres.py [Invio]
e si seguono le indicazioni. Occorre precisare la posizione del piano di galleggiamento, che dovrebbe essere
stata rilasciata in precedenza da Calcnav: se non la si ricorda più basta aprire il documento "dati.txt"
e leggere il valore del piano di galleggiamento in corrispondenza di 0°. Nell'esempio riportato in questa
guida esso vale circa 0,4886 m. Lo script legge il file delle pressioni fittizie, legge il file della mesh, e
risale alla posizione dei nodi delle facce costituenti la superficie esterna; per ogni faccia trova la profondità
del suo baricentro e, se essa risulta positiva (cioè la faccia stessa è sotto il pelo dell'acqua),
scrive la pressione corretta secondo la "solita" relazione
p = 9810 × profondità
e infine trascrive tale informazione nel nuovo file "scafo.pres", che si può finalmente adoperare per il calcolo.
Si può finalmente assemblare il documento "inp" che può essere passato al solutore: si tratta di un file di testo contenente la mesh,
i vincoli, i carichi, le caratteristiche del materiale costituente lo scafo, il campo in cui eseguire il calcolo (in questo esempio si considera il campo elastico). Questo si ottiene copiando e incollando in un unico file
il contenuto dei vari "all.msh", "scafo.pres", "bordo.spc" e aggiungendo per ciascuno l'intestazione della sezione rispettiva,
nonché i dati relativi al materiale. Per questa parte è necessario riferirsi con attenzione al manuale
ed agli esempi proposti.
In questo caso si è ottenuto "scafo.inp": esso è costituito da diverse sezioni, ciascuna individuata
da un titolo in carattere maiuscolo e preceduto da "*", contenenti tutti i dati necessari al
solutore (geometria, vincoli, carichi, materiali, impostazioni del calcolo).
Alla fine dei valori di pressione va aggiunta la forza di
gravità applicata a tutti gli elementi costituenti lo scafo:
Eall,GRAV,9.810,0.0,0.0,-1.0
può giovare ricordare che questa riga significa che a tutti gli elementi (set predefinito Eall) viene applicata
una forza per unità di volume di intensità 9,81 e diretta secondo il vettore (0,0,-1), cioè verso il basso.
Il contenuto di "scafo.inp" è il seguente:
*HEADING SCAFO PRODOTTO CON CALCNAV
*NODE, NSET=Nall
1, -8.99507e-01, -1.05000e+01, 1.85371e+00
2, -9.09373e-01, -1.05000e+01, 1.92685e+00
3, -6.06194e-01, -1.05000e+01, 1.95121e+00
4, -4.49754e-01, -1.05000e+01, 1.92685e+00
5, -8.96779e-01, -1.04955e+01, 1.85422e+00
6, -9.06623e-01, -1.04955e+01, 1.92723e+00
[...]
6912, 3.29028e-02, 9.41109e+00, 2.39561e+00
6913, 3.46319e-02, 9.41388e+00, 2.39499e+00
6914, 3.69320e-02, 9.38891e+00, 2.37646e+00
6915, 3.63611e-02, 9.41667e+00, 2.39437e+00
*ELEMENT, TYPE=C3D8, ELSET=Eall
1, 1, 2, 3, 4, 5, 6, 7, 8
2, 4, 3, 9, 10, 8, 7, 11, 12
3, 3, 2, 13, 9, 7, 6, 14, 11
4, 5, 6, 7, 8, 15, 16, 17, 18
5, 8, 7, 11, 12, 18, 17, 19, 20
6, 7, 6, 14, 11, 17, 16, 21, 19
[...]
4483, 6867, 6906, 6910, 6877, 6863, 6907, 6911, 6871
4484, 6877, 6910, 6912, 6879, 6871, 6911, 6913, 6875
4485, 6906, 6892, 6912, 6910, 6907, 6893, 6913, 6911
4486, 6863, 6907, 6911, 6871, 6862, 6909, 6914, 6870
4487, 6871, 6911, 6913, 6875, 6870, 6914, 6915, 6874
4488, 6907, 6893, 6913, 6911, 6909, 6897, 6915, 6914
*ORIENTATION, NAME=SO, SYSTEM=RECTANGULAR
1.000000,0.000000,0.000000,0.000000,1.000000,0.000000
*MATERIAL, NAME=ACCIAIO
*ELASTIC, TYPE=ISO
2.068000e+11, 3.300000e-01, 300.000000
*DENSITY
7.693000e+03,300.000000
*SOLID SECTION, ELSET=Eall, MATERIAL=ACCIAIO,ORIENTATION=SO
*STEP, INC=100
*STATIC,SOLVER=SPOOLES
1.000000, 1.000000, 1.000000e-05, 1.000000e+30
*BOUNDARY
1898, 3
1899, 3
1908, 3
2158, 3
[...]
4316, 3
4317, 3
4322, 3
*DLOAD
734, P3, 88.83936
736, P3, 244.362195
742, P3, 348.0416325
744, P3, 399.88503
750, P3, 399.88503
752, P3, 348.0416325
[...]
3384, P3, 146.5614
3389, P3, 733.6138725
3390, P3, 146.5614
Eall,GRAV,9.810,0.0,0.0,-1.0
*NODE FILE
U
*EL FILE
S,E
*NODE PRINT, NSET=Nall
U
*EL PRINT, ELSET=Eall
S,E
*END STEP
Naturalmente i puntini "[...]" sostituiscono i lunghi elenchi di punti ed elementi che costituiscono la mesh, e quelli dei vincoli (sezione "BOUNDARY) e carichi (sezione "DLOAD", cioè "distributed load", ovvero carichi distribuiti), tutti rilasciati automaticamente da cgx, come spiegato in precedenza.
A questo punto "scafo.inp" viene passato al solutore:
$ ccx scafo
Dopo un po' di tempo (a seconda delle caratteristiche del calcolatore e del dettaglio introdotto nella simulazione) si ottiene in uscita "scafo.frd", che contiene i risultati, visualizzabili ancora una volta con cgx, usato in modalità di postprocessore (parametro "-v").
$ cgx -v scafo.frd
Premendo con il pulsante sinistro del mouse nella finestra di cgx, fuori del riquadro del disegno,
si accede al menu da cui scegliere quali risultati vedere e in che modo. Fondamentalmente si scelgono
i tre "dataset" di spostamenti, tensioni e deformazioni, per ciascuno dei quali sono disponibili
diverse voci (si veda il manuale di cgx in proposito).
Nella figura, la distribuzione della tensione equivalente secondo Von Mises lungo lo scafo

Naturalmente questo stesso calcolo andrebbe eseguito in maniera più efficiente su mezzo scafo, introducendo opportuni vincoli sui nodi del piano di mezzeria per rispettare la simmetria.