SECTION PREMIÈRE

DE LA RÉSOLUTION DES ÉQUATIONS DU TROISIÈME  DEGRÉ

1. Comme la résolution des équations du second degré est très-facile, et n’est d’ailleurs remarquable que par son extrême simplicité, j’entrerai d’abord en matière par les équations du troisième degré, lesquelles demandent pour être résolues des artifices particuliers qui ne se présent pas naturellement.

Soit donc l’équation générale du troisième degré

et comme on sait qu’on peut toujours faire disparaître le second terme de toute équation en augmentant ses racines du coefficient du second terme divisé par l’exposant du premier, on pourra supposer d’abord, pour plus de simplicité, m = 0, ce qui réduira la proposée  à la forme

.

C’est dans cet état que les équations du troisième degré ont été d’abord traitées par Scipio Ferreo et par Tartalea, à qui l’on doit leur résolution ; mais on ignore le chemin qui les y a conduits. La méthode la plus naturelle pour y parvenir me paraît celle que Hudde a imaginée, et qui consiste à représenter la racine par la somme de deux indéterminées qui permettent de partager l’équation en deux parties propres à faire en sorte que les deux indéterminées ne dépendent que d’une équation résoluble à la manière de celle du second degré.

Suivant cette méthode on fera donc  x = y + z, ce qui étant substitué dans la proposée la réduira à celle-ci

qu’on peut mettre sous cette forme plus simple

Qu’on fasse maintenant ces deux équations séparées

on aura

,

et, substituant dans la première,

,

c’est-à-dire

.

Cette équation est à la vérité du sixième degré, mais comme elle ne renferme que deux  différentes puissances de l’inconnue, dont l’une a un exposant double de celui de l’autre, il est clair qu’elle peut se résoudre comme celles du second degré. En effet, on aura d’abord

,

et de là

.

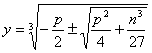Ainsi l’on connaîtra y e z, et de là on aura

.

2. Il se présente remarques à faire sur cette solution. D’abord il est clair que la quantité y doit avoir six valeurs, puisqu’elle dépend d’une équation du sixième degré ; de sorte que la quantité x aura aussi six valeurs ; mais comme x è racine d’une équation du troisième degré, on sait qu’elle ne peut avoir que trois valeurs différentes ; donc il faudra que les six valeurs dont il s’agit se réduisent à trois, dont chacune soit double. C’est aussi de quoi on peut se convaincre par le calcul, en éliminant  y des deux équations

[……………….]

De là il s’ensuit que la résolution d’une équation du troisième degré est, à proprement parler, la résolution d’une équation du sixième degré, inconvénient qui n’a pas lieu dans le second degré, dont la résolution est tout à fait propre à ce degré, mais qui devient encore plus considérable pour les équations des degrés supérieurs, comme on verra plus bas.

SEZIONE PRIMA

SULLA RISOLUZIONE DELLE EQUAZIONI DI TERZO GRADO

1. Poiché la risoluzione delle equazioni di secondo grado è molto facile, e non è d’altronde notevole che per la sua estrema semplicità, entrerò dapprima in argomento con le equazioni di terzo grado, le quali richiedono per essere risolte degli artifici particolari che non si presentano naturalmente.

Sia data quindi l’equazione generale di terzo grado

e siccome si sa che si può sempre far scomparire il secondo termine da ogni equazione aumentando le sue radici del coefficiente del secondo termine diviso per l’esponente del primo,  si potrà supporre inizialmente, per maggior semplicità,  m = 0, e ciò ridurrà l’equazione proposta alla forma       .

E’ in questa forma che le equazioni di terzo grado sono state inizialmente trattate da Scipione dal  Ferro e da Tartaglia, ai quali si deve la loro risoluzione; ma non si conosce il cammino che hanno seguito. Il metodo più naturale per risolverle mi sembra quello che ha immaginato Huddle e che consiste nel rappresentare la radice mediante la somma di due indeterminate che permettono di suddividere l’equazione in due parti adatte a fare in  modo che le due indeterminate non dipendano che da un’equazione risolubile alla stessa maniera di quelle di secondo grado.

Seguendo questo metodo si porrà dunque x = y + z, che essendo sostituita nell’equazione proposta la ridurrà a questa

che si può scrivere nella forma più semplice

Considerando ora queste due equazioni

si avrà

e, sostituendo nella prima,

,

cioè

Questa equazione è in verità di sesto grado, ma poiché contiene solo due differenti potenze dell’incognita , di cui una ha l’esponente doppio dell’altra, è chiaro che si può risolvere come quella di secondo grado. In effetti si avrà dapprima

e di qui

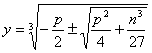
Così si conosceranno y e z, e da questo si avrà

.

2. Ci sono osservazioni da fare su questa soluzione. Innanzitutto è chiaro che la quantità y deve avere sei valori, poiché dipende da un’equazione di sesto grado; di modo che la quantità x avrà anch’essa sei valori;  ma poiché x è radice di una equazione di terzo grado, si sa che non può avere più di tre valori differenti; quindi è necessario che i sei valori di cui si tratta si riducano a tre, quindi ciascuno sia doppio. Di questo ci si può anche convincere mediante i calcoli, eliminando y dalle due equazioni

[……………….]

Da questo consegue  che la risoluzione di un’equazione di terzo grado è, a dirla schietta, la risoluzione di un’equazione di sesto grado, inconveniente che non ha luogo per il secondo grado, la cui risoluzione può essere fatta a questo stesso grado, ma che diventa ancora più considerevole per le equazioni di grado superiore, come si vedrà più avanti.