CARTESIO E LA NASCITA DELLA GEOMETRIA ANALITICA
Cartesio viene considerato il “padre” della geometria analitica. Tutti gli studenti delle superiori conoscono i termini ‘assi cartesiani’, ‘equazione cartesiana’. In particolare, il libro La Géométrie, pubblicato nel 1637 come appendice al Discours sur la méthode pour bien conduir sa raison et chercher la vérité dans les sciences, viene considerato il primo testo di geometria analitica. Tuttavia, se si cerca di approfondire la questione esaminando il testo, ci si accorge facilmente che in esso non vengono utilizzati esplicitamente gli assi, le coordinate dei punti, le equazioni delle curve… anche se è abbastanza facile riconoscere implicitamente l’uso di tali concetti. L’altro elemento importante che è molto evidente è il desiderio dell’autore di integrare l’algebra e la geometria.
Proviamo ad esaminare il primo brano de La Géométrie (libro secondo) in compaiono tali caratteristiche.
Je pourrois
mettre ici plusieurs autres moyens pour tracer et concevoir des lignes courbes
qui seroient de plus en plus composées par degrés à l’infini; mais pour
comprendre ensemble toutes celles qui sont en la nature, et les distinguer par ordre en certains
genres, je ne sache rien de meilleur que de dire que tous les points de celle
qu’on peut nommer géométriques, c’est-à-dire qui tombent sous quelque mesure
précise et exacte, ont nécessairement quelque rapport à tous les points d’une
ligne droite, qui peut être exprimée par quelque équation, en tous par une
même; et que,lorsque cette équation ne monte jusqu’au rectangle de deux
quantités indéterminées, ou bien au carré d’une même, la ligne courbe est du
premier et plus simple genre, dans leque il n’y a que le cercle, la parabole,
l’hyperbole et l’ellipse qui soient comprises; mais que lorsque l’équation
monte juaqu’à la troisième on quatrième dimension des deux, ou de l’une des deux quantités indéterminées
(car il en faut deux pour expliquer ici le rapport d’un point à un autre), elle
est du second; et que lorsque l’équation monte jusqu’à la cinquième ou sixième
dimension, elle est du troisìème; et ainsi des autres à l’infini.
Per ‘descrivere’ e classificare una curva (che può essere tracciata attraverso delle macchine), l’autore ritiene utile porre in relazione i punti della curva con i punti di una retta (vedere esempio successivo) e individuare l’equazione che lega tutti i punti della curva. Se questa equazione non ha termini di grado maggiore del secondo nelle due quantità incognite (noi diciamo le coordinate del generico punto) la curva è di I genere, cioè è una circonferenza, una parabola, un’iperbole o un’ellisse.
|
|
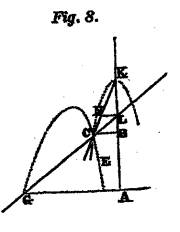
Comme si je veux savoir de quel genre est la ligne EC (fig.8), que j’imagine être décrite par l’intersection de la règle GL et du plan rectiligne CNKL, dont le coté KN est indéfiniment prolongé vers C, et qui, étant mu sur le plan de dessous en ligne droite, c’est-à-dire en telle sorte que son diamètre KL se trouve toujours appliqué sur quelque endroit de la ligne BA pro1ongée de part et d’autre, fait mouvoir circulairement cette règle GL autour du point G, à cause quelle lui est tellement jointe qu’elle passe toujours par le point L. |
Comincia la trattazione del I esempio. Usando dei termini un po’ più vicini al linguaggio matematico che utilizziamo oggi, possiamo “leggere” la definizione della curva in questo modo. La curva è il luogo geometrico dei punti C (Cartesio la indica con il termine “curva EC”). Gli elementi fissi della costruzione sono il punto G, attorno al quale ruota la retta GL, e il triangolo NKL, rettangolo in L, che trasla lungo la retta AB. La retta e il triangolo hanno in comune il punto L, quindi la traslazione del triangolo provoca la rotazione della retta GL.
Ciò premesso, C è definito come il punto d’intersezione fra la retta GL e la semiretta KN. Fino a qui, niente geometria analitica.
Je choisis une ligne droite comme AB, pour rapporter à ses divers points tous ceux de cette ligne courbe EC; et en cette ligne AB je choisis un point comme A, pour commencer per lui ce calcul. Je dis que je choisis et l’un et l’autre, à cause qu’il est libre de les prendre tels qu’on veut; car encore qu’il y ait beancoup de choix pour rendre l’équation plus courte et plus aisée, toutefois en quelle façon qu’on les prenne, on peut toujours faire que la ligne paroisse de même genre, ainsi qu’il est aisé à démontrer. Après cela prenant un point à discrétion dans la courbe, comme C, sur lequel je suppose que l’instrument qui sort à la décrire est appliqué, je tire de ce point C la ligne GB parallèle à GA, et pourceque CB et BA sont deux quantités indéterminées et inconnues, je la nomme l’une y e l’autre x; mais afin de trouver le rapport de l’une à l’autre, je considère aussi les quantités connues qui déterminent la description de cette ligne courbe, comme GA, que je nomme a, KL que je nomme b, et NL, parallèle à GA, que je nomme c;
Questa è la parte in cui Cartesio applica il nuovo metodo. L’autore scrive: “Scelgo una retta AB, per riferire ai suoi punti quelli della curva EC; e su questa retta scelgo un punto A, per iniziare da esso tale calcolo. Posso scegliere liberamente sia la retta che il punto perché, anche se ci sono molti modi per sceglierli in modo da rendere l’equazione della curva più breve e più facile, qualunque scelta si faccia, si può fare in modo che la curva sia sempre dello stesso genere, come si può facilmente dimostrare. Dopo di che, prendendo un punto C a piacere sulla curva, […], traccio da C la retta GB parallela a GA, e poiché CB e BA sono due quantità indeterminate e incognite, chiamo la prima y e la seconda x; per trovare la relazione fra queste quantità, prendo in considerazione anche le quantità note che determinano la definizione della curva, come GA che chiamo a, KL che chiamo b, e NL, parallelo a GA, che chiamo c.”
Detto con il nostro linguaggio, AB è l’asse x, A è l’origine dell’asse, e, dal contesto, è ovvio che AG è il “nostro” asse y. Naturalmente non è previsto che C(x,y) abbia coordinate negative: Cartesio non accetta numeri negativi (vedere algebra).
Come dati vengono assunti, coerentemente con la descrizione iniziale della curva, il centro di rotazione della retta GA( GA = a, quindi G(0;a)), e i cateti del triangolo NKL.
puis je
dis, comme NL est à LK, ou c à b, ainsi CB ou y est à BK, qui est par
conséquent ![]() : et BL est
: et BL est ![]() , et AL est
, et AL est ![]() . De plus, comme CB est à LB, ou y à
. De plus, comme CB est à LB, ou y à ![]() , ainsi GA ou a est à LA ou
, ainsi GA ou a est à LA ou ![]() ; de façon que, multipliant la seconde per la troisième,
; de façon que, multipliant la seconde per la troisième,
orn
produit ![]() qui est égale à
qui est égale à ![]() , qui se produit en
multipliant la première par la dernière: et ainsi l’équation qu’il falloit
trouver est
, qui se produit en
multipliant la première par la dernière: et ainsi l’équation qu’il falloit
trouver est
![]()
de
laquelle on connoit que la ligne EC est du premier genre, comme en effet elle
n’est autre qu’une hyperbole.
Dopo aver fissato le variabili e i dati, Cartesio cerca l’equazione della curva, sfruttando la similitudine fra i triangoli NKL e CBK e la similitudine fra i triangoli CLB e GLA:
NL : LK = CB : BK
quindi c : b = y : BK e di conseguenza ![]()
BL = ![]() , AL =
, AL =![]()
CB : LB = GA : LA quindi y : ![]() = a :
= a : ![]()
Applicando la proprietà fondamentale delle
proporzioni , si ottiene l’equazione della curva: ![]()
Cartesio riconosce che è un’iperbole.
Può essere interessante da un punto di vista didattico ritrovare l’equazione della curva con i metodi “nostri”, prendendo come parametro LA = t e/o “costruire” il luogo con qualche “macchina” moderna (p.es. utilizzare Cabri).