Questi sono appunti di una lezione svolta con una 4^ liceo scientifico-tecnologico. La seconda parte era relativa alla nascita della geometria analitica con Cartesio, in cui è stato esaminato (tradotto) il brano tratto da La Géometrié riportato in questo sito.

L’Algebra dai Greci a Cartesio

· I più antichi testi che riportano esempi di risoluzione algebrica di un’equazione completa di secondo grado sono del periodo babilonese antico e risalgono a circa 4000 anni fa.

· I Greci affrontarono le equazioni di I e II grado soltanto in modo esclusivamente geometrico. Per esempio l’equazione veniva impostata con la seguente formulazione “ Dato un segmento a e un’area b determinare quale altezza x deve avere un rettangolo di base a+x affinché la sua area sia uguale a b”. L’incognita x veniva poi trovata con una costruzione geometrica. [N.B. I termini letterali non erano usati dai Greci. Quello precedente è un esempio “tradotto” in termini moderni]. Lo sviluppo dell’algebra in Grecia fu molto inferiore a quello della geometria. I Greci utilizzarono unicamente i numeri razionali.

· Lo sviluppo dell’algebra riprese con gli Indiani e gli Arabi. La parola algebra deriva dal nome di un libro “Al-jabr wa’l muqabalah” scritto verso l’830 dal matematico Al-Khuwarismi, dal nome del quale deriva a sua volta il termine algoritmo. Nella sua opera egli introduce i principi di equivalenza delle equazioni e mostra i metodi risolutivi delle equazioni di I e di II grado. Agli Indiani e agli Arabi si deve l’introduzione dello zero, dei numeri negativi e della scrittura posizionale dei numeri.

· I risultati ottenuti dagli Arabi arrivarono in Europa attraverso le Crociate e gli scambi commerciali. Venne affrontata anche la risoluzione di equazioni di grado superiore al secondo. I problemi e le risoluzioni erano espressi senza simboli, unicamente a parole (algebra retorica). Non venivano accettate le soluzioni negative.

1° esempio. Riconoscete l’equazione e la formula risolutiva riportate nel testo seguente? [N.B. censo: quadrato dell’incognita, radice: l’incognita, numero: termine noto]

Quando vorrai trovare il valore del censo che con le radici assegnate sia uguale al numero dato, fai così: prendi il quadrato della metà delle radici e aggiungi il numero, come sopra dato, e di ciò che otterrai prendi la radice dalla quale togli il numero della metà delle radici e ciò che resterà sarà la radice del censo richiesto. [Leonardo Fibonacci, Liber abaci, 1202]

2° esempio. Provate a tradurre in linguaggio attuale l’equazione e la formula risolutiva riportate nel testo seguente. [N.B. cosa: incognita, cubi: cubo dell’incognita, numero: termine noto]

Il Capitolo di cose e cubo uguale al numero:

Quando le cose e li cubi si eguagliano al numero, ridurrai l’equazione a 1 cubo partendo per la quantità delli cubi, poi cuba la terza parte delle cose, poi quadra metà dil numero e questo suma con il detto cubato, et la radice di detta summa più la metà del numero fa un binomio et la radice cuba di tal binomio, men la radice cuba del suo residuo val la cosa. [Pompeo Bolognetti, Regole pricipali dell’Arte maggiore, 1554-1558]

· Furono scoperte le formule risolutive delle equazioni di terzo e quarto grado. Tali formule portarono però alla necessità di utilizzare nei calcoli intermedi numeri negativi e radici quadrate di numeri negativi, cioè dei numeri immaginari (introdotti dal bolognese Raffaele Bombelli nel 1572). Tali numeri non venivano tuttavia accettati come veri numeri, ma solo come ripiego per completare i calcoli e giungere così alle soluzioni positive.

1° esempio. Scritta con notazioni moderne la formula risolutiva dell’equazione di terzo grado è 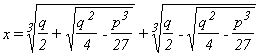. Se si applica questa formula all’equazio-ne , si ottiene (quindi radici di numeri negativi ....) e solo dopo calcoli inventati fatti con numeri che non esistono si arriva alla soluzione accettabile x = 4.

2° esempio. Per molto tempo i matematici non accettarono, se non come artificio di calcolo, i numeri che non fossero razionali positivi.

Per i numeri reali. Poiché, nel dimostrare le figure geometriche, quando i numeri razionali non ci bastano i numeri irrazionali prendono il loro posto e dimostrano esattamente quelle cose che i numeri razionali non potrebbero dimostrare [...] noi siamo spinti e costretti ad affermare che essi sono veramente numeri; siamo infatti costretti dai risultati che seguono dal loro impiego, risultati che percepiamo come reali, certi e costanti. D’altro canto, altre considerazioni ci costringono a negare che i numeri irrazionali siano affatto numeri. Infatti quando cerchiamo di assoggettarli alla numerazione [forma decimale] scopriamo che essi sempre si dileguano, cosicché non uno di loro può essere precisamente appreso in se stesso. [...] Ora, non può chiamarsi un vero numero ciò che per sua natura manca di precisione. [...] Perciò, come un numero infinito non è un numero, così un numero irrazionale non è un vero numero, ma qualcosa di nascosto in una specie di nuvola d’infinito. [ Michael Stifel, Arithmetica integra, 1544]

A proposito di radici negative. Per quanto sono in grado di giudicare, esse servono solo a confondere tutta la teoria delle equazioni e a rendere oscure e misteriose cose che per loro natura sono fin troppo chiare e semplici.[...] Le radici negative, perciò, non avrebbero mai dovuto essere ammesse in algebra, e bisogna sperare che ne vengano escluse: se ciò accadesse vi sono buone ragioni per immaginare che le obiezioni che molte persone dotate di ingegno muovono alle computazioni algebriche, affermando che esse sono oscure o complicate da concetti quasi inintelleggibili, verrebbero a cadere. [Francis Masères, Dissertation on the Use of the Negative Sign in Algebra, 1759]

A proposito di numeri complessi. Vediamo dunque che le radici quadrate dei numeri negativi non sono né maggiori né minori di zero. Né si può dire che siano zero [...] E’ chiaro che non si può neppure includere la radice quadrata di un numero negativo fra i numeri possibili, e bisogna dunque dire che è una quantità impossibile. E’ in questo modo che siamo condotti all’idea di numeri che per loro natura sono impossibili. Di solito questi numeri sono chiamati numeri immaginari, numeri non raffigurabili, perché esistono esclusivamente nell’immaginazione. [Euler, Algebra, 1770]

· Nella prima metà del XVII viene introdotta [finalmente!] l’algebra simbolica, nella quale vengono utilizzati dei simboli accettati e riconosciuti da tutti i matematici. La Géometrie (1637) di Cartesio è il più antico testo matematico che può essere letto ancora oggi senza incontrare difficoltà nel linguaggio e nel simbolismo.

· Solo nella prima metà del XVIII secolo i matematici accettarono il concetto di numero negativo.

Esempio . Ma delle Quantità altre sono positive, cioè maggiori del nulla, altre minori del nulla, e però negative. Per cagione d’esempio: I Beni che si posseggono, sono positivi, ma quelli, che ad altri si debbono, sono negativi, perché dai positivi s’hanno a sottrarre, e ne diminuiscono la somma, e però siccome sono quantità positive i Capitali, che uno abbia, così sono quantità negative i debiti. Similmente se un Mobile diretto verso uno scopo, o meta del suo viaggio descriva uno spazio positivo; ma se si porterà dalla parte opposta, descriverà uno spazio, che relativamente alla meta, verso cui doveva andare, sarà negativo. Quindi in Geometria se una linea condotta da una parte si assuma per positiva (il che è arbitrario) sarà negativa la linea condotta dalla parte opposta. [Maria Gaetana Agnesi, Istituzioni analitiche, 1748] .

INDIETRO