Serie di Fourier
Di Massimo Fantin 2001
Uso del programma di simulazione
Lo sviluppo in serie di Fourier permette di eseguire l'interpolazione trigonometrica ovvero consente di approssimare una funzione periodica di periodo T mediante la somma di una costante e le f unzioni trigonometriche di periodo multiplo di T.
Se la funzione f(x) data ha periodo 2p , potrà essere scritta :
f (x) = a0+a1 cos (x) + b1 sin (x) + a2 cos (2 x) + b2 sin (2 x) + a3 cos (3 x) + b3 sin(3 x) + .....
Per determinare i coefficienti si usano le seguenti formule:
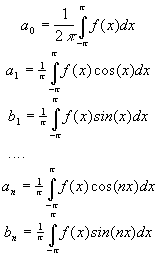
Ad ogni funzione f(x) integrabile tra -p e p corrisponde una determinata serie trigonometrica. Se la serie trigonometrica converge uniformemente essa è la serie di Fourier , la somma coincide con la f(x) quasi dappertutto, se poi la f(x) è continua la convergenza avviene in tutto l'intervallo [-p , p ].
Se la serie è di soli coseni la funzione è pari, viceversa se e di soli seni la funzione è dispari.
Esempi di sviluppi in serie di Fourier
Dente di sega
Y = x / 2 = sin x - sin(2x)/2 + sin(3x)/3 - sin(4x)/4+.....
Onda quadra
Y = p sgn x /4 = sin x +sin(3 x) /3 + sin(5 x) /5 + ..... ( dove sgn indica il segno sgn(x) = 1 se x >0 sgn (x) = -1 se x <0 sgn(0) = 0 )
Onda triangolare
Y=p /4 *(p /2 - x) = cos(x) + cos (3 x) /32 + cos(5 x)/52+..........
Uso del programma di simulazione
La funzione di cui si vuole scrivere e rappresentare lo sviluppo si scrive in alto secondo le stesse regole delle funzioni del programma specifico.
Il significato dei tasti in basso sono :
i tasti zoom per modificare le dimensioni dell'immagine
il tasto sviluppo per attivare o disattivare sia la rappresentazione grafica delle funzioni componenti in blu che la loro espressione analitica.
I tasti su e giu che spostano la scrittura della rappresentazione trigonometrica della funzione.
I tasti o+ e o- che modificano l'ordine di approssimazione, fermando la rappresentazione della curva approssimata in verde all'ordine richiesto.
I tasti n+ ed n- che modificano il numero dei punti nei quali viene calcolata la funzione data, viene rappresentata assieme alle approssimazioni. Il numero n è multiplo di 2 il valore massimo è 1024, naturalmente, più è basso il numero n più è veloce ma è anche meno preciso.
Il tasto parametro che permette di modificare il valore del parametro k che può figurare nell'espressione della funzione.
La rappresentazione della funzione data è rossa, dell'approssimazione è verde e delle componenti è blu.
Il grafico può essere trascinato con il mouse.
La rappresentazione delle funzione indicata si considera periodica di periodo [-p , p ]
Le tre funzioni degli esempi dati nella parte teorica diamo la rappresentazione:
Sin 2x =1-2Sin2 x
Se scriviamo 1-2*(sx)^2 vediamo, calcolando lo sviluppo che si tratta della funzione sin(2x)
Per esempio
Se vogliamo trasformare l'espressione :
sen 4x * cos 3x + cos 3x - 5 cos 2x
si può digitare
s(4*x)*c(3*x)+(cx)^3-5*c(2*x)
e aumentare l'ordine di approssimazione fino a quando il grafico rosso della funzione risulta invisibile perché ad esso è sovrapposto dalla sua approssimazione leggiamo che tale funzione è uguale a
3/4 cos x + 1/2 sen x - 5 cos 2x + 1/4 cos 3x + 1/2 sen 7x
la verifica a mano può essere eseguita con un po' di pazienza.