
di Massimo Fantin 2005
Home
Il problema dei tre corpi consiste nello studio del moto di tre masse che si attirano secondo la legge di gravitazione di Newton. Non è possibile risolverlo in modo esatto, si può studiare in modo numerico. Lo scopo di questo lavoro è quello di risolvere il problema semplificato nel piano, supponendo cioè che i tre corpi si muovano sullo stesso piano nel piano. Per fare questo occorre impostare un sistema di equazioni differenziali nelle incognite le funzioni che rappresentano per ciascuna massa: le due coordinate spaziali x, y e le due velocità nelle direzione degli assi v, w. in tutto quindi dodici equazioni differenziali.
Supponendo per semplicità di scegliere unitario il valore della costante di gravitazione universale il sistema è il seguente:

dove gli indici i,j,k assumono in successione i valori 1,2,3 2,3,1 3,1,2.
Per risolvere tale sistema in 12equazioni differenziali si utilizza il metodo di Runge Kutta del quarto ordine. L'incognita è il vettore dodicidimensionale X = ( x1,y1,v1,w1,x2,y2,v2.w2,x3,y3,v3,w3) e la funzione di trasformazione F( x1,y1,v1,w1,x2,y2,v2.w2,x3,y3,v3,w3) è data dalle dodici funzioni espresse dai secondi membri del sistema scritto precedentemente.
Il sistema, vettorialmente si scrive
X' = F(X)
alla quale dobbiamo aggiungere la condizione iniziale X0 che contiene in sé le posizioni e le velocità iniziali delle tre masse.
L'algoritmo di risoluzione consiste nei seguenti passaggi: si parte da uno stato iniziale Xo e
per via ricorsiva si passa dal vettore Xn al vettore successivo Xn+1 mediante i seguenti passaggi che fanno riferimento all'intervallo di tempo dt tra due stati successivi del sistema e i vettori K1,K2,K3,K4
K1=dt*F(Xn)
K2=dt*F(Xn+K1/2)
K3=dt*F(Xn+K2/2)
K4=dt*F(Xn+K3)
Xn+1=Xn+K1/6+K2/3+K3/3+K4/6
Il metodo usato è particolarmente efficace nello studiare un fenomeno come questo infatti è possibile seguire il movimento dei corpi celesti nelle loro orbite.
Per poter osservare in modo efficace le soluzioni del problema dei tre corpi ho supposto che il centro di massa fosse fisso nell'origine , questo significa che le condizioni iniziali del sistema si riducono di quattro valori, che nel caso particolare erano le coordinate x,y,v,w del corpo di massa maggiore.
Ho voluto studiare alcuni casi particolari:
Quando i tre corpi celesti sono simili a Sole Terra Luna, La massa del Sole è enormemente maggiore di quella della Terra e la massa della Terra è diverse volte più grande di quella della Luna.
Interessante è lo studio dei punti lagrangiani nel caso semplificato in cui una delle tre masse sia trascurabile rispetto alle altre due che si muovono di moto circolare intorno al loro baricentro.
I punti lagrangiani sono cinque, tre di essi L1, L2 L3 si trovano sull' asse del sistema, ovvero sulla retta che congiunge le masse maggiori dette primarie, L1 si trova tra tra le masse, L2 esternamente, dalla parte della massa minore e L3 è esternamente dalla parte della messa maggiore.
I punti lagrangiani sono punti nei quali le forze gravitazionali dovute ai corpi maggiori producono in una massa secondaria posta in essi l'accelerazione centripeta necessaria affinché detto terzo corpo si muova di moto circolare uniforme solidale con il moto delle masse primarie.
Per calcolare posizione dei punti lagrangiani L2 ed L3 si impone quanto detto sopra:
Siano rA, ed rB i raggi delle orbite delle masse mA ed mB.
Sia w la velocità angolare del sistema dei corpi primari, dalle equazioni di Newton uguagliando la forza centripeta al'attrazione gravitazionale prodotta dall'altro corpo primario si ha:
mB w2 rB = G mA mB / (rA+rB)2
mB w2 rA = G mB mA / (rA+rB)2
da cui si ricava il valore della velocità angolare
w2 = G mA / ( rB (rA+rB)2 ) = G mB / ( rA (rA+rB)2 )
Dalla costanza del centro di massa nell'origine segue che la masse sono inversamente proporzionali ai raggi : mA/mB = rA/rB
Ponendo x il raggio di rotazione della massa secondaria, imponendo la condizione secondo la quale l'accelerazione dovuta alla forza gravitazionale dei due corpi primari sia uguale all'accelerazione centripeta si ottiene:
G mA / ( x + rA)2 + G mB / ( x - rB)2 = x w2 = x G mA/ ( rB( rA+ rB )2 )
Semplificando, eliminando la massa mB e supponendo per semplicità che la distanza delle masse primarie sia unitaria, ovvero ponendo
b = rB / (rA + rB )
si ottiene la seguente equazione di quinto grado nel parametro b che rappresenta la distanza relativa di uno dei due pianeti primari dal centro di massa e la x rappresenta il raggio di rotazione del punto lagrangiano.
b(x-y)2+(1-b)(x+1-b)2-x(x+1-b)2(x-b)2 = 0 (L23)
Questa equazione può essere usata per determinare sia L2 che L3 a seconda che 0.5< b<1 0< b <0.5.
In modo analogo si può calcolare il punto L1, modificando semplicemente l'equazione, si ottiene:
b(x-y)2 - (1-b)(x+1-b)2-x(x+1-b)2(x-b)2 = 0 (L1)
Entrambe le equazioni trovate L12, L1 , nel caso 0 < b < 1, ammettono una sola soluzione che può essere trovata con il metodo di Newton partendo da 1 per L23 e partendo da 0 per L1.
I punti lagrangiani quarto e quinto L4, L5 non si trovano sull'asse di rotazione ma nel terzo vertice di un triangolo equilatero di base le masse primarie.
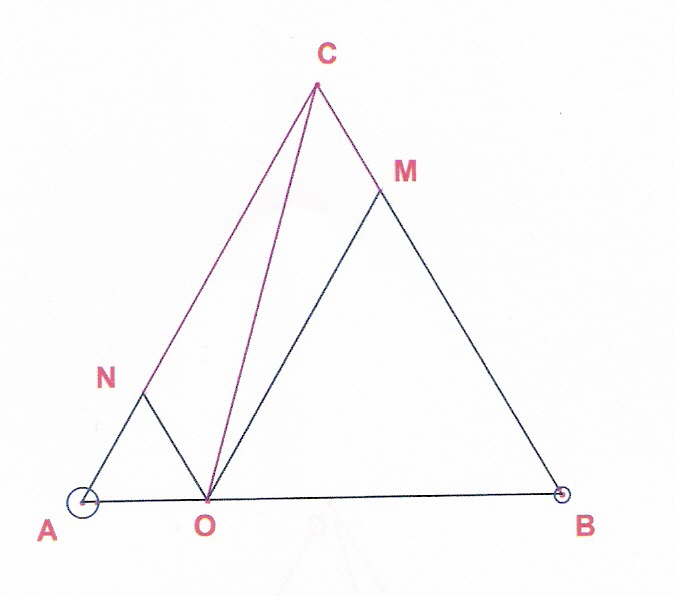
Il grafico rappresenta in A e B le sue masse primarie, nel punto O il centro di gravità
il vettore AO rappresenta l'accelerazione che la massa in
B esercita su A,
il vettore BO rappresenta l'accelerazione che la massa in A esercita
su B.
analogamente i vettori CN e CM rappresentano le accelerazioni che che le masse
in A e B esercitano sulla massa C, da notare che le accelerazioni prodotte, a
differenza delle forze non dipendono dalla massa che viene accelerata ma solo
dalla massa accelerante, inoltre le distanze delle tre masse sono uguali.
la somma di dette accelerazioni è data da CO. che rappresenta il raggio
vettore della massa secondariA.
Si calcola infine la distanza di C dal centro di gravità r = rA2 + rB2 + rArB mentre la velocità angolare è la stessa dei punti A e B.