RITORNA

Vogliamo trovare una dimostrazione geometrica, usando il piano di Minkowski delle formule dell'effetto Doppler relativistico.

Supponiamo l'emettitore in moto con velocità v verso il rispetto al ricevente, sia T₀ (rispetto al suo sistema di riferimento)

Il tempo tra un'emissione e l'altra o il periodo del segnale trasmesso, per il ricevente il tempo tra la ricezione di un segnale e l'altro sarà T=T₀/ Ö (1-v²) dove come al solito si è considerata unitaria la velocità della luce c=1 e si suppone che la velocità della trasmissione sia uguale a quella della luce c.

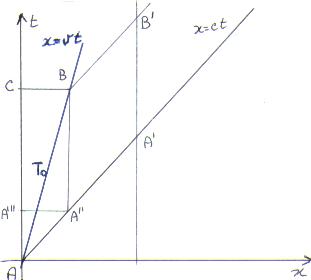
Possiamo rappresentare i moti nel seguente diagramma:

Esaminando il diagramma poniamo T₀ =AB il periodo dell'onda trasmessa nel sistema di riferimento in moto. Il periodo dell'onda ricevuta A' B', se tracciamo un segmento ad esso parallelo A"B, otteniamo il trapezio ACBA" nel quale la base minore rappresenta il periodo dell'onda ricevuta dal ricevente la base maggiore AC= T₀/ Ö(1-v²) e la diagonale AB=T_0.

Si ha che CB= v T₀/ Ö (1-v²) , ricordiamo infatti che v=tg(BAC) ,

Ma CB=A" A"' da cui, osservando che A"A è la bisettrice degli assi , si avrà che anche AA"' =CB, pertanto il periodo del ricevente sarà:

T = A"B=AC-AA"'= T₀/ Ö (1-v²)-v T₀/ Ö (1-v²) = T₀ (1-v)/ Ö (1-v²) = T₀ Ö ((1-v)/(1+v)).

Se poi vogliamo togliere la clausola c=1 basterà sostituire v con v/c ottenendola solita formula dell'effetto doppler relativistico, che si trova sui libri:

T = T₀ Ö ((c-v)/(c+v)).

Se supponiamo che la sorgente sia in allontanamento si può fare una costruzione analoga seguendo lo schema:

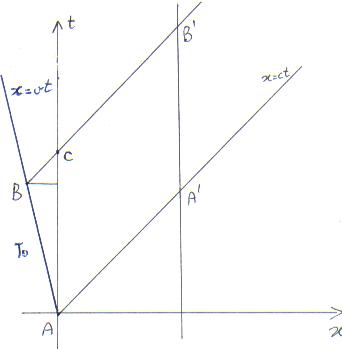
E si otterrà:

T=T₀/Ö (1-v²) + v T₀/Ö (1-v²) = T₀ Ö ((1+v)/(1-v)).

E analogamente, nel caso in cui c non sia 1

T = T_{0 Ö} ((c+v)/(c-v)).

Si può fare una costruzioni analoga per studiare il caso in cui la velocità di propagazione del segnale sia inferiore quello della luce, in tal caso sia v la velocità della sorgente e V la velocità di propagazione dei segnali, si dovrà tracciare

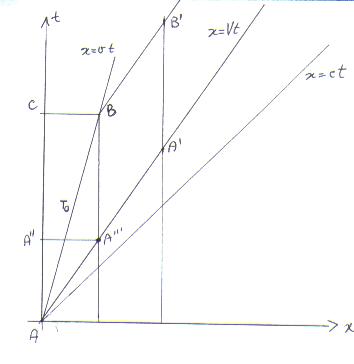
AC=T=T₀/Ö (1-v²), analogamente a come fatto sopra BC = v AC, mentre AA"= A"A"'/V

B'A'=BA"'=AC-AA"=AC-A"A"'/V da cui

T= T₀/Ö (1-v²)-v/V*T₀/Ö (1-v²) = T₀(1-v/V) /Ö (1-v²).

Nel caso in cui c non si consideri unitaria la formula diventa:

T= T₀(1-v/V) /Ö (1-v²/c²).

Si osserva che, nel caso v sia molto piccola rispetto alla velocità della luce c diventa:

T=T₀(1-v/V) ovvero si ritrova la formula classica.

RITORNA