Lezione 8a
*Il principio di conservazione del quadrimomento*
Consideriamo una rezione in cui due particelle A e B collidono producendo le particelle C e D (chiaramente C e D possono coincidere con A e B, ma possono anche essere diverse)
La precedente reazione viene scritta tramite l'espressione
In relatività l'unico principio di conservazione che assumiamo è:
(1)
ovvero: Le 4 componenti del quadrimomento del sistema sono conservate
Ovviamente il principio di conservazione del quadrimomento comprende il principio di conservazione dell'energia (m=0) e il principo di conservazione della quantità di moto (m=1,2,3).
Alcune applicazioni del principio di conservazione del quadrimomento
______________
Consideriamo due particelle A e B entrambe di massa a riposo m, le quali si muovono lungo la direzione x con velocità +v e -v (a<1). Ammettiamo che queste particelle collidano frontalmente e diano origine ad una particella C di massa M secondo la reazione
 |
(1) |
Cosa possiamo dedurre dalla conservazione del quadrimomento?
Il quadrimomento delle particelle A e B è rispettivamente
, 
Mentre il quadrimomento della particella C deve essere del tipo
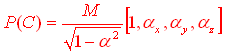
La relazione (1) si traduce scrivendo le 4 condizioni
, ay=0,
az=0
Da cui si ricava in maniera elementare
a = 0
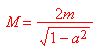
Quindi nell'urto frontale di due particelle identiche la massa della particella nel canale d'uscita è in quiete e la sua massa è superiore alla somma delle masse iniziali.
_________________________
Consideriamo ora una particelladi massa M inizialmente a riposo; questa decade in due particelle di massa identica m secondo la reazione:
Cosa ci dice il principio di conservazione del quadrimomento?
La parte che indica la conservazione del quadrimomento permette di ricavare in maniere quasi elementare v(A) = -v(B), ovvero le particelle A e B si allontanano con velocità opposta di modulo |v|
Il principio di conservazione dell'energia ci permette invece di scrivere
Da cui si ricava, sapendo che a=0
v = (1-(2m/M)2)1/2
Ovviamente la precedente equazione ha senso se la massa della particella a riposo è superiore alla somma delle masse delle particelle nel canale d'uscita. In caso contrario la reazione non può aver luogo.
Indice Lezioni - Lezione Precedente - Lezione Seguente