|
Ci soffermiamo un momento a parlare di energia (potenziale e cinetica) dal punto di vista fisico. Quindi vedremo come questa entra in gioco nel volo di un aereo di carta o di un aereo comunque senza motore. Considerazioni in questo senso possono anche influire sul progetto, in base al tipo di volo che si vuole ottenere. Campo di forze e Potenziale - Energia Potenziale Si è visto che nei pressi della Terra esiste un campo gravitazionale, per il quale, in ogni punto dello spazio, sulla massa unitaria agisce una forza inversamente proporzionale al quadrato della distanza del punto dal baricentro della terra. In realtà questa forza risente anche della rotazione terrestre. Nei problemi pratici che ci interessano e nell'ambiente che ci interessa si può considerare questa forza come costante e pari (su massa unitaria di 1 kg) a 9,81 N/kg. Si è visto come questo numero corrisponda anche alla accelerazione di gravità (9,81 m/s²). Se un punto di massa M si sposta nel campo, le forze del campo eseguono un lavoro. Se questo lavoro dipende solo dai punti iniziale e finale dello spostamento, allora il campo si dice "conservativo". Senza starlo a dimostrare, il campo gravitazionale è conservativo. In un campo conservativo può essere definita in ogni punto una funzione Potenziale V(x, y, z). Vediamo come, senza addentrarci in ragionamenti "per addetti ai lavori".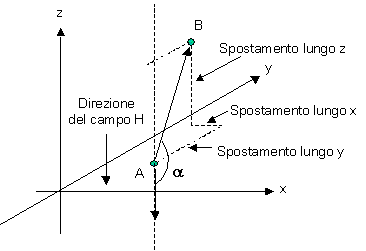 
Sappiamo che una forza compie un lavoro quando il punto materiale a cui è applicata si sposta nella direzione della forza, o comunque faccia uno spostamento che abbia una componente non nulla nella direzione della forza. Il lavoro fatto è appunto il prodotto della forza per questa componente dello spostamento (matematicamente si dice che il lavoro è il prodotto "scalare" della forza per lo spostamento).Abbiamo appena finito di dire che il campo gravitazionale è conservativo, e quindi il lavoro delle forze del campo non dipendono dal percorso fatto, ma solo dai punti iniziale e finale. Allora consideriamo la figura in cui sono rappresentati due punti A e B nel campo suddetto e vediamo quale è il lavoro delle forze del campo per spostare una massa unitaria da A a B. Potendo scegliere un percorso qualsiasi, ci spostiamo secono le tre componenti del tratto A-B. Nei tratti Dx e Dy le forze del campo non compiono lavoro in quanto sono perpendicolari a questi spostamenti. Nel tratto Dz invece la forza e lo spostamento sono paralleli e quindi si ha il lavoro (ci si riferisce sempre alla massa unitaria) L = H Dz. Questo lavoro è negativo in quanto la forza si oppone allo spostamento (il campo H è diretto in senso contrario allo spostamento). Se indichiamo con Dr lo spostamento complessivo rappresentato dal segmento A-B si ha anche che Dz = r ·cos a dove a è l'angolo tra spostamento e campo (ecco il prodotto scalare L = H x Dr). Se ora da B torniamo in A, il lavoro fatto sarà ancora lo stesso, ma questa volta con segno positivo, perchè le forze del campo sono concordi con lo spostamento Dz. Il lavoro totale diventa allora L - L = 0 ed infatti il lavoro totale per andare da A ad A è nullo in quanto il lavoro "speso" nella prima parte è "restituito" nella seconda. Si definisce allora Potenziale del campo una funzione V (x, y, z), definita in ogni punto del campo, tale che per una massa unitaria che si muove da A a B si abbia L = Va - Vb = - DV. Si è visto come, nell'ambito di nostro interesse, gli spostamenti orizzontali non facciano lavoro e quindi non cambino il valore del potenziale, il quale viene a dipendere solo dall'altezza. Superfici orizzontali sono allora dette superfici "equipotenziali". Abbiamo anche visto come calcolare il valore del lavoro passando da una all'altra di queste superfici. Abbiamo in realtà definito una "Differenza di Potenziale" che è quanto ci interessa, in quanto gli spostamenti che ci riguardano avvengono sempre tra due superfici equipotenziali. Se prendiamo come riferimento la superfice su cui ci troviamo (prato, pavimento, etc.) e che limita il nostro spazio verso il basso, possiamo definire un potenziale rispetto a questa superfice, che varia solo con l'altezza h sulla superfice stessa (coordinata z del riferimento precedente). Ora vediamo quanto vale questo potenziale: Sollevando una massa qualunque M di una altezza h [metri], la forza applicata g·M [Newton] compie un lavoro L = -g·M·h [Newton per metri] . Se dividiamo questo valore per la massa (consideriamo quindi l'azione su massa unitaria) otteniamo il potenziale del punto raggiunto, rispetto al potenziale del punto di partenza che vale allora V = -L = g·h [N m / kg]. Possiamo scrivere in questo modo se assumiamo come zero il potenziale del piano di riferimento. In questo modo, dicendo "potenziale V di un punto", in realtà sottointendiamo "differenza di potenziale tra un punto ed il nostro riferimento". Se una massa generica M si trova ad una altezza h nel campo gravitazionale, è sulla superficie di potenziale g h. Il campo applica la forza g M. Se la massa è libera di cadere fino alla superfice di riferimento, il lavoro fatto è L = g M h. La capacità di compiere lavoro che ha una massa M che si trova ad un potenziale V è quindi data da Ep = V M e si chiama Energia Potenziale della massa M e si misura in [N m] = [Joule]. Anche in questo caso occorre fare attenzione a descrizioni che considerano come unità di misura delle forze il kilogrammo-peso. Energia Cinetica Nel paragrafo precedente si è visto (e si è detto esplicitamente) come l'energia sia posseduta (o associata) da una massa e corrisponda a capacità di compiere lavoro. Se tiriamo una pietra dentro un vetro, questa compie un lavoro (e un bel lavoro, ... vandali!..), che non è associato alla sua altezza, ma alla sua velocità. Questa energia è associata ad un "campo di forze"? La domanda non ci tocca e procediamo in modo più semplice. Supponiamo che una massa M sul piano di riferimento di cui sopra abbia una velocità iniziale verso l'alto pari a v0 e che non vi siano altre forze che qulle del campo gravitazionale. Fin dove sale la massa? Il che significa: che lavoro viene fatto in conseguenza della velocità iniziale? Sappiamo che sulla massa agisce l'accelerazione di gravità -g (diretta verso il basso). La cinematica ci dice che la velocità, in questo caso, varia in funzione del tempo secondo l'espressione v = v0 + a t = -g t ed il lavoro che cerchiamo termina quando v diventa zero (massima altezza raggiunta). Sappiamo anche che lo spazio percorso nel tempo t in questo caso è h = v0 t + (1/2) a t² = v0 t - (1/2) g t².  Qui a lato viene riportata la determinazione di quanta energia potenziale viene acquistata dalla massa M come conseguenza della sua velocità iniziale v0, ciò significa che si determinai il lavoro fatto contro le forze del campo utilizzando questa velocità, in altre parole l'energia Ec associata a questa velocità, la cui espressione è riportata, e che si chiama Energia Cinetica, denominazione che significa appunto "energia di movimento". Si può affermare che l'energia cinetica iniziale della massa si è trasformata in energia potenziale. Quando la massa si ferma, la sua energia cinetica si è azzerata e l'energia potenziale ha raggiunto il suo massimo. Se la massa ricade, succede evidentemente il processo contrario e l'energia potenziale si trasforma in energia cinetica. In ogni punto ed in ogni istante del moto della massa, la sua energia totale rimane costante (si suppone che non vi siano forze parassite) ed è la somma Et = Ep + Ec che corrisponde alla velocità ed altezza in quel punto ed in quell'istante. Situazione energetica iniziale del volo (Lancio del velivolo) Una premessa iniziale, che ci complica le cose, è che in questo discorso non si può trascurare la resitenza dell'aria, che è essenziale nel determinare la durata e la velocità del volo. Esiste quindi una quota di energia che viene trasferita continuamente dal velivolo all'aria circostante che viene messa in moto dal velivolo stesso che vi passa attraverso. Del resto è su questo che si basano le azioni aerodinamiche. Supponiamo che il volo si svolga in aria ferma e facciamo l'ipotesi che l'assetto del velivolo al momento del lancio sia quello di equilibrio. Le variabili del lancio sono allora: 1) - L'altezza h da terra (potenziale di riferimento) a cui il velivolo è lanciato. 2) - La velocità v0 iniziale impressa al velivolo dal lanciatore. 3) - L'angolo l che questa velocità forma con l'orizzontale. Una opportuna combinazione dei valori di questi tre fattori produce un determinato "tipo di lancio". Normalmente il lancio viene effettuato "a mano", ma non si escludono altri metodi, come ad esempio un lancio "fiondato" ad elastico. In ogni caso ci riferiamo ad un "punto di lancio" intendendo il punto in cui cessa sul velivolo l'azione del "dispositivo" di lancio ed il velivolo stesso inizia il suo volo libero. Il velivolo ha una massa Mv ed una velocità v0. Inoltre si trova ad una altezza h. La sua energia totale è quindi Et = g Mv h + (1/2) Mv v0² e questo indipendentemente dall'angolo a cui viene lanciato. La resistenza aerodinamica di un velivolo viene qui indicata con R v², dove R rappresenta il fattore, che viene assunto costante, che moltiplicato per il quadrato della velocità produce la effettiva forza che si oppone al moto. Specifichiamo ancora due termini che ci sono utili e cioè ve che è la velocità di planata in equilibrio come visto alla pagina precedente e vor che è la velocità richiesta dal modello in assetto di equilibrio per volare orizzontale, cioè con la portanza che compensa esattamente il peso. A titolo di esempio consideriamo l'aereo progettato nella precedente pagina e supponiamo che la sua velocità sia di 6 m/s, anzichè quella di equilibrio di 3,5 m/s, e che sia lanciato orizzontalmente (angolo di lancio l = 0). Inizialmente non vi è alcuna forza di trazione, e la resistenza aerodinamica, alla velocità di lancio, è di circa R v² = 18 mN. La massa del velivolo è Mv = 5,122 [g]. Questo significa che al velivolo è applicata una decelerazione iniziale di circa a = -3,5 m/s². Questo non significa che in un secondo la sua velocità si riduca di 3,5 m/s, poiché appena la velocità diminuisce, anche la resistenza e quindi la decelerazione diminuiscono. Riprenderemo in seguito questo esempio. Esaminiamo alcuni casi di lancio con alcuni tipi di velivolo. Il discorso sarà piuttosto qualitativo, in quanto il problema della resistenza funzione del quadrato della velocità non è facilmente trattabile analiticamente. È possibile comunque realizzare un programma di simulazione per descrivere questo tipo di volo, non particolarmente complicato se ci si limita a considerare un volo che si svolge in un piano verticale. Il programma non è comunque stato realizzato. e se ne utilizza solo al tecnica per dare qualche indicazione delle grandezze in gioco. Dopo il lancio Planata semplice Si ottiene lanciando un velivolo, da una altezza h, con l'angolo di planata di equilibrio e la velocità di equilibrio ve corrispondente. Si ottiene un volo discendente rettilineo come visto a proposito della planata. L'energia iniziale è data come sempre da Et = g Mv h + (1/2) Mv v0² e si è visto che durante il volo l'energia cinetica Ec non varia in quanto la velocità non varia. L'energia potenziale Ep diminuisce di g Mv v sin(l) ogni secondo. Questa è la quantità di energia al secondo (Potenza) che il velivolo dissipa nell'aria, che la assorbe mettendosi in moto. Lancio orizzontale con velocità ve = vor Al punto di lancio il velivolo è in equilibrio su di una traiettoria orizzontale, ma non ha forza di trazione. Nel primo intervallino elementare dt dopo il tempo T0 del lancio, la sua velocità si è ridotta di -a dt dove a = Forza / Massa = R v0² / Mv . A questo punto la portanza P v² (con P definito analogamente ad R) non è più sufficiente a sostenere l'aereo in volo orizzontale e la differenza tra la forza peso e la portanza G - P v², agendo sulla massa dell'aereo provoca una accelerazione verso il basso ed una conseguente componente verticale vv della velocità v. Questo determina un aumento dell'assetto del velivolo rispetto al flusso e quindi l'intervento del momento totale Mt che aumenta verso il basso l'angolo l della traiettoria. A questo punto nasce una trazione G sin(l) che inizia ad opporsi alla resistenza. Questo meccanismo, in teoria, prosegue fino a quando non si raggiungono l'angolo e la velocità di equilibrio, per poi proseguire come nel caso precedente. Se e come angolo e velocità sono raggiunti dipende comunque da altre caratteristiche del velivolo. Infatti: 1) - La differenza tra peso e portanza, applicata alla massa del velivolo provoca una accelerazione verso il basso che, comunque, è contrastata da una resistenza dell'aria, funzione della velocità al quadrato, che dipende dalla sagoma del velivolo. Questa accelerazione provoca la componente verticale della velocità. 2) - Il Momento che tende a far ri-orientare l'aereo, applicato al Momento di Inerzia secondo l'asse trasversale, provoca una accelerazione angolare che a sua volta genera una velocità angolare (che parte da 0) che a sua volta provoca la variazione dell'angolo di assetto. Il velivolo può tendere più o meno rapidamente alla situazione di equilibrio, oppure più raggiungera, superarla ed oscillarvi intorno in diversi modi. (stabilità dinamica). Tipi di velivolo In quanto segue distinguiamo due tipi di aerei, "pesanti" e "leggeri", anche se poi non è facile assegnare uno specifico modello ad una delle due categorie. Una delle differenze è la quantità di energia cinetica di cui l'aereo può disporre al momento del lancio, poichè il lancio a mano suppone una velocità iniziale comunque limitata. Facciamo anche un'altra distinzione in tipi "veloci" e tipi "lenti", intendendo i primi come aerei che hanno una planata piu "picchiata" dei secondi in quanto, a differenza di questi, richiedono una più alta velocità per volare. I primi sfruttano meglio l'energia cinetica, i secondi l'energia potenziale. Lancio in caduta verticale 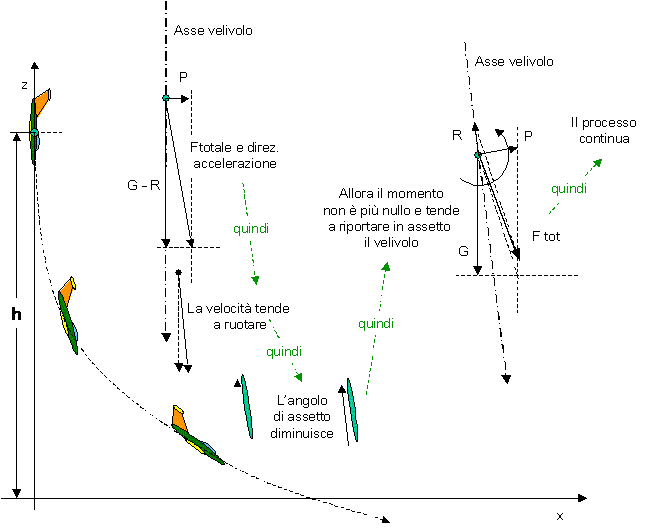 È una prova interessante per classificare tentativamente il tipo di aereo. Si suppone di avere a disposizione una altezza h sufficente (per ora non limitata). Il velivolo viene tenuto nell'assetto di equilibrio rispetto ad un ipotetico flusso verticale dal basso (a muso in giù) e lo si lascia cadere con velocità v0 = 0. La sua accelerazione iniziale è -g = -9,81 [m/s²], ma appena inizia il movimento si sviluppa la resistenza e l'accelerazione decresce. In questa posizione la portanza non è compensata dal peso, che invece si oppone alla resistenza e la vince largamente. Appena si sviluppa la portanza, il baricentro del modello inizia a deviare dalla verticale. Questo provoca una componente della velocità (piccola) diretta orizzontalmente e quindi la velocità del flusso, opposta a quella del velivolo, ruota nel senso di diminuire l'angolo di assetto. A questo punto interviene il momento totale del velivolo che tende a riportare l'aereo in assetto e ne devia l'asse dalla verticale. Questo è rappresentato in figura. Il processo cintinua fino a quando la somma totale delle forze agenti (Peso, Portanza, Resistenza) non si annulla. A questo punto si annulla anche il momento e l'aereo raggiunge l'assetto stabile di planata come visto nella pagina precedente. Ovviamente valgono anche in questo caso le considerazioni di stabilità dinamica fatte precedentemente. La posizione di equilibrio si raggiunge normalmente dopo una caduta piuttosto lunga (alcuni metri), ma già nella prima fase la curvatura della traiettoria è più o meno accentuata. Tentativamente si può dire che aerei che cadono "a picco" vanno bene per lanci veloci (sfruttano meglio l'energia cinetica) mentre aerei che tendono rapidamente a sollevarsi vanno meglio per lanci "in planata" (sfruttano meglio l'energia potenziale). Lancio con l positivo e v0 >> vor  È il tipo di lancio più interessante. L'energia totale Et dell'aereo è tale da potergli fare iniziare la planata da un punto più alto di quello del lancio. L'aereo ha la possibilità di sfruttare la sua energia cinetica per salire, ma è necessario che non si venga a trovare in stallo una volta raggiunta la sua altezza massima. La cosa infatti provocherebbe una forte perdita di quota in caduta prima di avere la possibilità di riprendere la planata. Sempre tentativamente, si dice che si sfrutta al massimo questo tipo di lancio quando si imprime al velivolo la velocità che corrisponde a quella di equilibrio sulla traiettoria avente inclinazione pari all'angolo l di lancio. Ovviamente non è facile ottenere in pratica questa velocità (non esistono "tachimetri da braccio"). Si può comunque dire che, data la massima velocità di lancio di cui è capace il braccio di un lanciatore e dato un determinato tipo di aereo, esiste un angolo di lancio per il quale la distanza percorsa dal velivolo è massima. A questo punto si nota che, se la massa del velivolo è alta, a parità di sagoma e quindi di resistenza, data una certa velocità iniziale, il velivolo rallenta nell'aria meno di un velivolo con massa piccola, in quanto la resistenza è applicata ad una massa maggiore e quindi produce una decelerazione minore. Il tratto percorso con eccesso di energia (nel senso precedente) è più lungo. Di conseguenza, però, sembra ragionevole che si accorci il tratto percorso in planata, in quanto questa ha una velocità di equilibrio superiore, il che fa supporre un angolo superiore. In realtà questo è da verificare, in quanto un peso maggiore richiede sì una portanza maggiore, ma a parità di angolo provoca anche una forza di trazione maggiore, in grado di opporsi ad una resistenza maggiore (e abbiamo supposto che la sagoma sia ancora la stessa, quindi la resistenza maggiore deriva dalla velocità maggiore). |
Via Pietro Micca a Torino. 
