|
Ora ci si occupa di aerei senza motore, capaci solo di sfruttare l'energia del lancio, la quota a cui si trovano e l'atmosfera stessa con i suoi fenomeni per poter volare. Nel caso poi di aerei di carta, l'altezza da terra e l'energia del lancio sono le uniche risorse che possono essere sfruttate. Gli alianti veri, ed anche i modelli "grossi" da gara hanno ancora la possibilità di sfruttare le correnti d'aria ascensionali o termiche che si sviluppano nell'atmosfera in determinate condizioni. Essenziale comunque è sapere come un aereo senza motore può planare (essenziale si fa per dire, c'è chi vive benisimo anche senza saperlo). I termini usati Giusto per non fare confusioni e non ripetere ogni volta lunghe e contorte frasi di spiegazione, che servono di solito a confondere le idee anziché chiarirle, precisiamo il significato dei termini che vengono usati nel seguito, ed i relativi simboli. Questi possono essere diversi da quelli usati finora, nella foga del discorso. Angolo di planata r Angolo tra l'orizzontale e la traiettoria del baricentro del velivolo. Lo contiamo come negativo quando l'aereo scende. Angolo di assetto a Angolo tra la direzione del flusso d'aria e l'asse longitudinale del velivolo. Positivo se l'aria incide sul ventre del velivolo. Angolo di montaggio alarem Angolo tra l'asse longitudinale e la corda alare. Positivo se il bordo di attacco è più alto. Angolo di incidenza alare y Angolo tra il flusso d'aria e la corda alare, positivo se il flusso investe l'intradosso. Angolo di montaggio stabilizzatore s Angolo tra l'asse longitudinale e la corda stabilizzatore. Positivo se il bordo di attacco è più alto. Angolo di incidenza stabilizzatore t Angolo tra il flusso d'aria e la corda stabilizzatore, positivo se il flusso investe l'intradosso. Angolo di calettamento k Differenza tra gli angoli di montaggio. Positivo se l'ala ha angolo maggiore dello stabilizzatore Le forze in gioco sono indicate con una lettera maiuscola quando sono intese come totali o risultanti. La stessa lettera maiuscola seguita dalla lettera minuscola v indica la componente verticale positiva se diretta verso l'alto. La maiuscola seguita dalla lettera minuscola o indica la componente orizzontale, positiva se nella direzione della componente orizzontale del moto. La maiuscola seguita dalla lettera minuscola t indica la componente nella direzione della traiettoria, positiva se nel verso del moto. La maiuscola seguita dalla lettera minuscola n indica la componente normale alla traiettoria, positiva se nella direzione verso l'alto. Eventuali altre componenti vengono definite al bisogno. G è il peso del velivolo P è la portanza totale R è la resistenza totale I momenti eventualmente usati vengono definiti in dettaglio al bisogno. L'assetto 
Per lo studio della planata è utile accompagnare la descrizione teorica ad un esempio. Lo studio è condotto in modo grafico secondo una idea che dovrebbe funzionare (essendo "logica" in senso matematico). Supponiamo quindi di disporre dei dati relativi ai profili usati per ali e stabilizzatori e di disporre delle caratteristiche costruttive del velivolo. Nella figura a fianco sono riportate le curve caratteristiche approssimate dei profili Clark Y (piano-convesso) e Naca 0009 (biconvesso simmetrico), ricavate da qualche vecchia rivista e trovate tra i miei appunti di progettazione (mi pare di ricordare che erano stati misurati a bassi numeri di Reynolds (per i nostri scopi vanno bene in ogni caso).Nel seguito supponiamo le caratteristiche costruttive di un aereo di carta e quindi i dati di profilo sono giusto teorici, per illustrare il metodo di studio. La precisione ottenibile con la carta, alle dimensioni considerate, esclude la possibilità di calcoli più o meno precisi (senza parlare del numero di Reynold). Il metodo è comunque applicabile ad aerei più grossi e precisi. Dati costruttivi dell'aereo considerato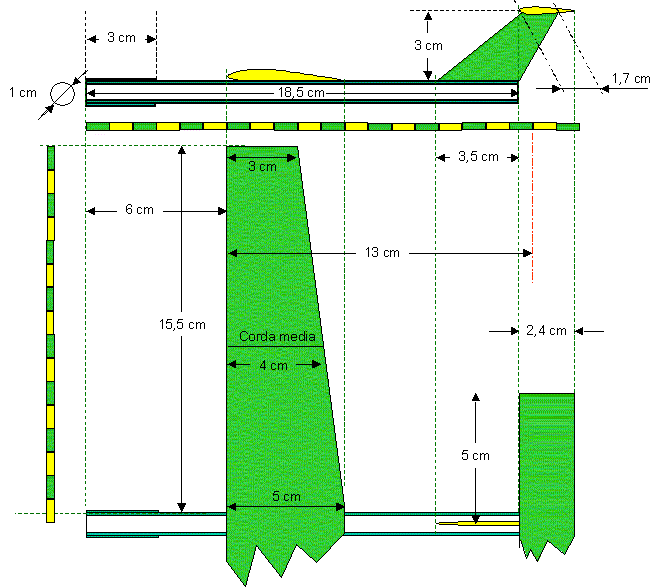 
La figura riporta la geometria dell'aereo. La carta di cui si suppone fatto è del tipo 80 gr/m², che corrisponde ad 8 mg per centimetro quadrato. La fusoliera è costituita da un tubo di carta a due strati a spirale del diametro di 1 cm ed è lunga 18,5 cm. La superfice di carta usata è quindi 116,18 cm² con una massa di 930 mg, a cui si aggiungono circa 10 mg di colla (quando asciutta), per un totale di 940 mg ed una forza peso di 9,221 mN applicati a 9,25 cm dal muso.Sulla parte anteriore del tubo troverà posto una striscia di carta larga 3 cm, che avrà la lunghezza necessaria ad equilibrare l'aereo, che verrà successivamente calcolata. La superfice Sa utile dell'ala per i calcoli aerodinamici è di 0,0124 m²;, mentre la superficie di carta per fabbricarla, tenuto conto che l'estradosso è più lungo di 1,5 mm e che sul bordo di uscita vi è una linguetta di 2 mm, risulta di 260 cm² che corrispondono ad una massa di 2,08 g e con la colla in totale 2,1 g. Quindi la forza è di 20,6 mN, ed il baricentro, la cui costruzione grafica non è riportata, si trova a 8 cm dal muso. Il timone di direzione ha baricentro a 18 cm dal muso e superficie di 2 x 7,8 cm², più 2 cm² di linguette di fissaggio. La sua massa totale è di 164,8 mg ed il suo peso di 1,8 mN considerando anche gli incollaggi. Infine il piano di coda ha baricentro a 20,6 cm dal muso, una superficie aerodinamica sc di 0,0024 m², superficie carta di 51 cm²; e massa totale, colla compresa, di 420 mg e peso di 4,12 mN. La forza peso totale del modello non centrato risulta di 35,74 mN, mentre il suo baricentro si trova a 10,3 cm dal muso. La posizione è, al momento, sicuramente troppo arretrata. Per prima cosa occorre scegliere un angolo di calettamento ed una incidenza alare di lavoro, tali che sia possibile ottenere condizioni di stabilità, cioè che vi sia un segmento in cui possa cadere il baricentro. Come primo tentativo si considerano tutti gli angoli a 0 gradi. In queste ipotesi si prova a disegnare il diagramma di Crocco.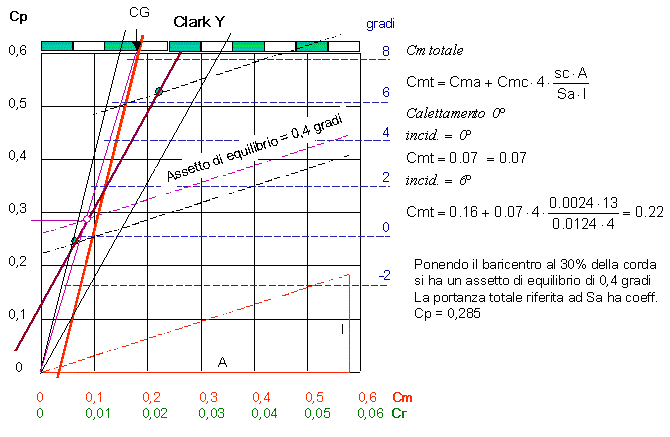 
Dal diagramma risulta che il calettamento scelto può andare bene. Si fissa la posizione del baricentro CG al 30% della corda media. In questo modo l'assetto di equilibrio risulta di +0,4 gradi, al quale corrisponde una portanza riferita all'ala di coefficiente Cp = 0,285. Ovviamente questi valori sono soggetti alla precisione con cui il disegno può essere fatto, alla precisione con cui vengono determinati i punti di incrocio delle linee, e così via.Occorre allora, innanzitutto, portare il baricentro del velivolo nella posizione decisa. Questo viene fatto avvolgendo una striscia di carta, sempre dello stesso tipo, larga 3 cm e lunga quanto basta (vedi calcolo successivo) sul muso del modello, come indicato nella figura che riporta il disegno costruttivo. Quanto deve essere lunga la striscia? Sappiamo che: Il baricentro deve cadere a 7,33 cm dal muso. Al momento una forza 35,74 mN è applicata a 10,3 cm dal muso. Il baricentro della striscia verrà a trovarsi a 1,5 cm dal muso. La forza peso totale G, data dai 35,74 mN e dal peso della striscia, si deve trovare a 7,33 cm dal muso. Questo significa: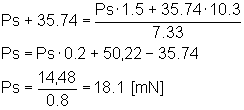 
Ma 18,1 mN corrispondono ad una massa di 1,85 g e quindi ad una superficie della nostra carta pari a 231,25 cm². Essendo la striscia larga 3 cm, la lunghezza risultante sarebbe pari a 77 cm circa. Un avvolgimento di questo tipo costituirebbe una notevole sezione frontale, con aumento di resistenza aerodinamica molto alto, nonché un pessimo effetto estetico.Conviene allora modificare la struttura, facendo un avvolgimento di larghezza 4 cm, messo a sbalzo sui due primi centimetri di fusoliera. Si ricalcolano le distanze dei baricentri trovati dal nuovo muso, che risulta avanzato di 2 cm rispetto al precedente. I 35,74 mN risltano allora applicati a 12,3 cm dal muso ed il baricentro della stiscia è a 2 cm, mentre il baricentro totale deve cadere a 9,33 cm dal nuovo muso. Quindi: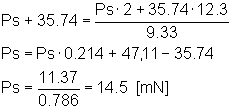 
La massa di carta da aggiungere si riduce ad 1,48 g. Tenendo conto anche della colla, occorrono 1,4 grammi di carta corrispondenti a 175 cm². Con la srtiscia di 4 cm la lunghezza corrispondente risulta di circa 44 cm. Non si può dire che il problema sia ben risolto, ma va già meglio. La forza peso totale G del velivolo risulta di 50,25 mN.Ora occorre stabilire la resistenza totale del velivolo nell'assetto calcolato. Questo lo facciamo nelle ipotesi semplificate viste in precedenza e relative alla resistenza di fusoliera. Inoltre, per non complicare troppo le cose, supponiamo che i dati dei profili siano stati ottenuti con l'allungamento utilizzato dal modello (nessuna necessità di correzione). Per l'aria consideriamo la densità r = 1,2. Per la fusoliera scegliamo il coefficiente di resistenza 0,12 riferito alla sezione maestra (dovrebbe essere ragionevole) e lo consideriamo costante, ottenendo una resistenza Rfus = 0,00015 v² [N] = 0,15 v² [mN] (approssimando la sezione maestra ad 1 cm²). Per il timone di direzione (superfice 0,00078 m² ad incidenza 0 gradi) la resistenza è Rtim = 0,0000084 v² [N] = 0,0084 v² [mN]. L'ala, ad incidenza 0,5 gradi ha resistenza Rala = 0,00028 v² [N] = 0,28 v² [mN] Infine lo stabilizzatore, anch'esso a 0,5 gradi di incidenza ha resistenza Rstb = 0,000056 v² [N] = 0,056 v² [mN] La resistenza totale diventa allora R = 0,0004944 v²[N] = 0,4944 v² [mN] Si è visto che la portanza totale ha coefficiente 0,285 e questo porta ad una portanza totale P = 0,00424 v² [N] = 4,24 v² [mN]. La planata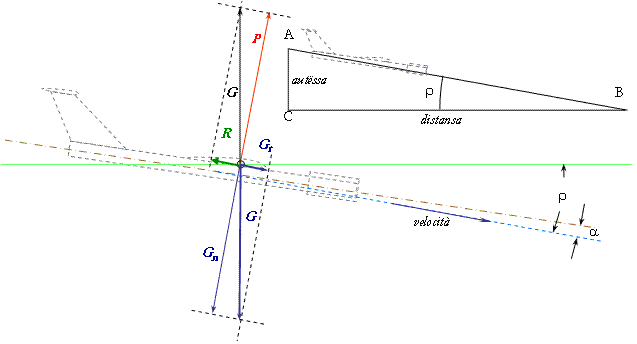 
La figura rappresenta le forze, e loro componenti, che agiscono sul velivolo nella traiettoria di planata, che in equilibrio supponiamo rettilinea.La forza peso G si scompone in due componenti. Una, Gt, è parallela alla traiettoria e una, Gn, è normale alla traiettoria. La portanza totale P calcolata, si riferisce alla direzione normale alla traiettoria. mentre la resistenza R calcolata è parallela alla traiettoria. In equilibrio, la componente Gt del peso compensa la resistenza R che ha segno contrario, e pertanto avremo che Gt + R = 0, altrimenti il velivolo accelererebbe o rallenterebbe. Anche la componente Gn, che è negativa, è compensata dalla portanza P, in modo che Gn + P = 0, altrimenti l'angolo di planata aumenterebbe o diminuirebbe. Si vede subito dalla figura che il triangolo fatto adi lati G, P, R ed il triangolo ABC sono simili (hanno tre angoli uguali) e dunque l'angolo r vale r = arctan (R / P) . Il rapporto R / P è la pendenza della traiettoria, e vale anche AC / CB cioé (altezza / distanza) , che è l'inverso dell'efficenza E. Nel nostro esempio possiamo dire che 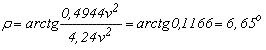 . In questo modo possiamo trovare, per esempio, la componente del peso Gn che deve essere compensata dalla portante P. Abbiamo:
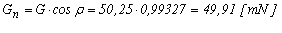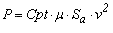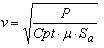 e questa deve essere la portanza.Ma la portanza, come abbiamo visto, ha espressione  e dunque l'espressione della velocità sarà  Nel caso del nostro esempio si ottiene 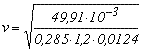 dove sono state usate le unità di misura del sistema S.I. Facendo i conti si ottiene, per il modello, una velocià v = 3,43 [m/s].sviluppando questo discorso, e tenendo anche conto dell'uguaglianza Gt + R = 0, senza fare tutti i passagi, possiamo trovare una espressione per la componente verticale della velocità (quota perduta al secondo), che, con qualche semplificazione, risuta essere 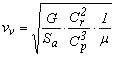 Il primo fattore sotto radice é quello che si chiama "carico alare" (rapporto tra peso e superfice alare, dunque peso per unità di superfice). Il secondo fattore si rende utile per stabilire quale deve essere l'assetto (che dipende dalla posizione del baricentro), notando che l'assetto più favorevole è quello che rende minima l'espressione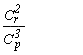 
|
Piazza Solferino a Torino.. 
