|
Si richiamano qui solo alcuni concetti, che nel corso della trattazione successiva sarebbe poi difficile richiamare. Servono anche per partire con le idee chiare. Il Sistema MKS - Massa e Peso È un sistema di misura (atto a descrivere le grandezze fisiche della meccanica), che utilizza tre unità di misura fondamentali: Il Metro per le lunghezze Il Kilogrammo per le masse Il Secondo per il tempo Tutte le altre grandezze meccaniche sono derivate da queste fondamentali (ad esempio la velocità verrà espressa in metri su secondi - m/s -). Il metro misura le lunghezze e viene definito in vari modi, sempre più precisi, con misure ripetibili in modo sempre più uguale ed esatto. A noi basta sapere che qualunque "metro" è capace di misurare una lunghezza, ed un buon righello millimetrato sarà sufficiente ai nostri scopi. Non vi sono ambiguità, tra la gente comune, sulla sua definizione (tutti sanno cos'é). Grosso modo corrisponde alla quarantamilionesima parte dell'equatore terrestre (adesso sì che mi faccio una idea "chiara" di quanto è lungo!). Il secondo misura il tempo e viene anche lui definito in vari modi, come per il metro. Anche in questo caso ci basta l'idea intuitiva che abbiamo. Grosso modo corrisponde alla ottantaseimilaquattrocentesima parte del giorno medio, ma per averene una idea più precisa basta guardare la lancetta dei secondi di un orologio (purché non sia fermo). Il kilogrammo, invece, si presta a molti equivoci che derivano dalla esperienza giornaliera e che possono fare sbagliare vistosamente i calcoli. Abituati a considerarla una misura di peso, è invece una misura di massa. L'equivoco nasce anche dall'esistenza di un sistema cosidetto "pratico", che effettivamente usa come unità fondamentale non la massa ma la forza-peso. Io sono un fisico e quindi non uso questo sistema, ma molte tabelle di manuali (in particolare se vecchi) danno i dati in queste unità pratiche ed occorre fare attenzione a come si usano. La massa di un oggetto materiale è la quantità di materia che lo costituisce e non cambia in funzione del luogo e dalla situazione in cui l'oggetto si trova (in Fisica Classica). Il peso, invece, cambia, ed è la forza che il campo gravitazionale applica alla massa dell'oggetto, sommata alle altre forze che l'ambiente può applicare (ad esempio la spinta di Archimede del fluido (aria, acqua) in cui l'oggetto è immerso. Si assume come unità di massa "pratica" quella di un decimetro cubo di acqua distillata a 15 gradi centigradi (un kilogrammo). La massa si "rende nota" allo sperimentatore attraverso due differenti caratteristiche, che fanno definire due "aspetti" della massa stessa: la massa gravitazionale e la massa inerziale. Il primo aspetto è legato al fatto che due masse si attraggono. La forza con cui si attraggono è direttamente proporzionale a ciascuna delle due masse ed inversamente proporzionale al quadrato della loro distanza (o meglio, della distanza dei loro baricentri). Si può quindi pensare che una massa, nello spazio, generi un "campo di forze" (definito in ogni punto come la forza che agisce sull'unità di massa) che agisce su ogni altra massa attirandola con la forza detta. Il nostro ambiente di esperienza comune è molto vicino ad una massa enorme (rispetto alle masse da noi conosciute per esperienza), che è il pianeta Terra. Sperimentiamo che ogni massa è attratta verso il centro della terra con una data forza. Poichè siamo comunque molto lontani dal centro della terra, nei pochi metri dei nostri esperimenti non possiamo notare che la forza varia, in quanto la distanza dal centro della terra varia di troppo poco per misurarne gli effetti con strumenti usuali. Per i problemi pratici non si commettono errori avvertibili se si considera questo campo come costante. L'aspetto inerziale della massa, invece, è legato alla nostra esperienza che quando la forza totale che agisce su una massa è diversa da zero, allora la massa varia la sua velocità. Questa variazione di velocità (o accelerazione), è proporzionale alla forza ed inversamente proporzionale alla massa. Questo permette di definire l'unità di misura della forza, che si chiama Newton e si indica con [N]. Un newton è la forza che applicata alla massa unitaria [1 kg] provoca una variazione di velocità costante di un metro al secondo ogni secondo. Per avere il valore di accelerazione occorre considerare la variazione complessiva della velocità e dividerla per i secondi in cui è avvenuta (differenza tra velocità finale meno velocità iniziale, divisa per il tempo in cui è avvenuta). La grandezza che viene misurata è allora espressa in [m / s2], unità di misura della accelerazione. A sua volta il Newton, espresso in unità fondamentali, è [kg · m/s²]. Ritorniamo adesso al campo gravitazionale terrestre. Ogni massa presente nel nostro ambiente subisce una attrazione verso il centro della terra, una forza che tende a farlo cadere e che, se è libera di agire, dà alla massa una accalerazione. Questa forza è quello che si chiama il peso della massa. 
Se sosteniamo un oggetto con la mano, avvertiamo questa forza sulla mano stessa, appunto come peso dell'oggetto, il quale sta fermo poiché la nostra mano applica, a spese dei nostri muscoli, una forza uguale e contraria che azzera la forza totale. Se togliamo la mano ed abbandoniamo il peso (supponendo di poter trascurare la resistenza dell'aria), osserviamo il peso cadere aumentando la sua velocità, quindi a causa di una accelerazione. Se misuriamo questa accelerazione otteniamo circa 9,81 [m / s2], qualunque sia l'oggetto che cade (in un tubo verticale dove si sia tolta l'aria, una piuma cade allo stesso modo di una pallina di piombo). Ma l'accelerazione (espressa in metri su secondo al quadrato) che una massa subisce non è altro che il rapporto tra la forza che agisce (espressa in Newton) e la massa (espressa in kilogrammi). Allora su di una massa di un kg agisce una forza peso di 9,81 N.Questa è anche la definizione del campo gravitazionale terrestre (forza su unità di massa), che coincide con l'accelerazione di gravità, indicata di solito con g. La figura completa ed illustra quanto detto. In conclusione, quando diciamo che un dato oggetto pesa un kilo, in realtà intendiamo che l'oggetto in questione ha massa tale da subire una attrazione di forza 9,81 N e che quindi ha massa di un kilo. L'oggetto in realtà quindi "pesa" 9,81 Newton. Questo modo pratico di parlare di peso vale solo dove e quando l'accelerazione di gravità può essere considerata costante e pari a 9,81 m / s². La Pressione Quando una forza agisce in modo "distribuito" su di una superficie, si definisce "Pressione" la forza che agisce sulla unità di superficie. La pressione si misura quindi in [N / m²]. Tra i vari tipi di pressione, quella che qui interessa è la pressione esercitata dall'aria atmosferica su una superficie. Si sa che l'aria è un miscuglio di gas (noi semplifichiamo dicendo che è un gas). I gas tendono ad occupare tutto lo spazio che hanno a disposizione, perchè allora l'aria rimane intorno alla terra e non si disperde nello spazio? Anche l'aria ha la sua massa che, quindi, viene attratta dalla massa della terra. Perchè allora l'aria non si deposita molto più densa sulla superficie della terra? I gas sono comprimibili se una qualche forza li costringe in uno spazio più piccolo. Ma il gas compresso contrasta questa forza esercitando una pressione sulle superfici del volume in cui viene compresso. Il risultato della nostra atmosfera è l'equilibrio tra la forza applicata dalla gravità che tende a comprimere l'aria sulla superficie terrestre e la pressione dell'aria stessa, che tende ad espanderla verso lo spazio. La pressione dell'aria (come la pressione di ogni fluido) si esercita in ogni direzione ed è sempre perpendicolare alla superficie su cui si esercita. Il peso che l'atmosfera applica ad un metro quadrato di superficie (pressione) è dato dal peso della colonna d'aria che sovrasta quel metro quadrato (supposto orizzontale). Al livello del mare si tratta di ben 101363 [N/m²]. Più alta è la pressione, più massa d'aria è "compressa" nell'unità di volume e quindi più l'aria "pesa". Salendo in quota la pressione quindi diminuisce in modo non lineare. Inoltre i gas che compongono l'aria hanno peso diverso, e quindi varia anche la loro presenza percentuale. Quanto detto si riferisce alla pressione statica dell'aria, ma qui interessano di più i fenomeni dinamici che provocano variazioni locali di pressione rispetto a quanto visto. Punto di partenza è una semplificazione del celebre teorema di Bernoulli. Le considerazioni fatte qui partono da principi generali e sempre validi, ma sono condotte in modo semplificato e le conclusioni valgono quando le velocità in gioco sono molto inferiori alla velocità del suono. Ma perchè proprio la velocità del suono? Supponiamo di avere un cilindro a tenuta con uno stantuffo e di cambiare istantaneamente la posizione dello stantuffo. Nelle nostre considerazioni semplificate supponiamo che istantaneamente la pressione nel cilindro cambi di conseguenza. Questo in realtà non è vero. Si forma, nelle vicinanze del pistone, un picco di pressione che si propaga come un'onda nel cilindro e lo stato di equilibrio si raggiunge dopo un certo tempo. Ma che cosa è il suono? Nient'altro che una serie di picchi di pressione intervallati da picchi di depressione (onda) che si propagano nel fluido, ad una velocità che, guarda caso, è quella del suono (la sua). Se le onde di pressione si propagano a velocità inferiori alle velocità in oggetto, le conclusioni dei ragionamenti (molto più complessi) sono decisamente diverse. Per velocità che siano decisamente inferiori a quelle del suono, le conclusioni semplificate sono molto bene approssimate e possono essere ritenute esatte.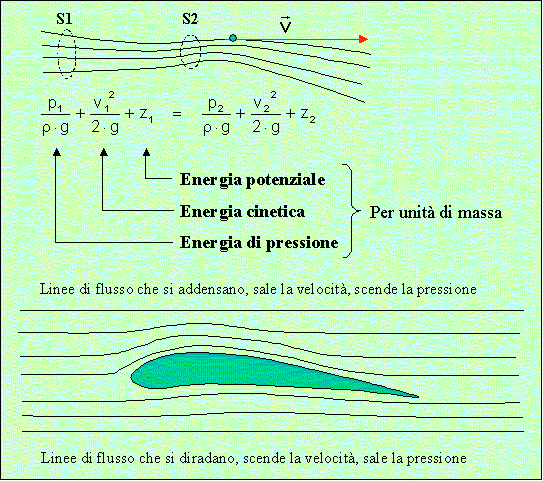 
Il teorema di Bernoulli è una delle forme in cui si esprime il principio generale di conservazione dell'energia. La figura riporta le espressioni matematiche di quanto viene detto, senza darde dimostrazione (piuttosto complessa). Il risultato che cerchiamo, infatti è una giustificazione "logica" alle espressioni che saranno usate nel seguito, le quali saranno supportate dal metodo sperimentale. Consideriamo il moto "stazionario" di un fluido, cioè il moto in cui in ogni punto la velocità del fluido non cambia nel tempo. In ogni punto dello spazio interessato è allora definito un vettore di velocità tangente alla linea percorsa da una particella fluida. Una sezione S normale al flusso individua un insieme di linee di flusso che costituiscono un "tubo di flusso"m all'interno del quale il fluido si comporta come in un vero tubo. Questo tubo non ha in generale sezione costante (ad esempio a causa di presenza di ostacoli). Scrivendo la relazione di conservazione dell'energia per una massa unitaria di flusso che corre lungo il tubo, si dice che la sua energia di pressione sommata a quella cinetica, sommata a quella potenziale (energia totale) deve rimanere costante per ogni sezione del tubo. Se la sezione si restringe, poiché la portata del tubo è costante, la sua velocità deve aumentare, cosa evidente dall'infittirsi delle linee di flusso (come per tutti i campi, il campo velocità è più intenso laddove le linee di campo sono più fitte). Allora, se l'energia potenziale non cambia (moto orizzontale) deve diminuire la pressione. Viceversa succede se le linee di campo si diradano a causa di un allargamento della sezione del tubo di flusso. Il disegno mostra le linee di flusso quando il fluido investe un ostacolo (che, guarda la combinazione, nel nostro caso ha il profilo di un'ala). Le linee fitte superiori indicano una diminuzione di pressione, quelle rade inferiori un aumento di pressione. Sulle due facce del profilo, allora vi è una differenza di pressione, quindi una differenza tra le forze applicate dalla pressione stessa alle superfici dell'ala. In questo caso la forza è diretta verso l'alto, che è il risultato che si vuole ottenere con un'ala. Il Numero di Reynold Questo numero è un importante fattore in aerodinamica. L'aspetto di questo numero che ci interessa è enunciato qui di seguito, considerando comunque che esso ha anche altri significati. Innanzitutto diciamo che il moto di un fluido ha due regimi fondamentali. Il primo, analogo a quello descritto sopra, è il moto laminare, nel quale le particelle di fluido seguono linee di flusso come quelle descritte, come se si trattasse di "lamine" di flusso che si mantengono individuabili e separate, sebbene a contatto. Il secondo è il moto turbolento, nel quale le particelle seguno traiettorie vorticose e non possono essere individuate lamine che si mantengono separate, in quanto queste si spezzano e si mescolano. Lo stabilirsi di uno dei due regimi dipende dalla natura del fluido, dalla sua velocità e dalle dimensioni degli oggetti con i quali il fluido interagisce. Una opportuna combinazione di questi fattori porta a stabilire un numero, detto di Reynold. Ad ogni situazione corrisponde quindi un valore di questo numero, mentre situazioni diverse possono avere numeri di Reynold simili o uguali. Per quanto ci riguarda e ci servirà dopo, l'importanza di questo numero è che si dimostra che nelle situazioni sperimentali in cui vengono misurati gli effetti aerodinamici, i risultati che si ottengono sono applicabili a tutte le situazioni analoge purché ad esse corrispondano numeri di Reynol uguali o vicini a quelli delle situazioni di misura. Questo fa sì che misure effettuate su un dato profilo alare con un modello di qualche metro quadrato e velocità del fluido di alcune centinaia di metri al secondo, non siano a priori valide per lo stesso profilo utilizzato su un modello di pochi decimetri quadrati e velocità di un paio di decine di metri al secondo. Occorre prima calcolare i due numeri di Reynold e quindi misurare la variabilità dei risultati al variare di questo numero, prima di stabilire se, e con quale approssimazione, i risultati delle misure sono applicabili. La densità Un rapido richiamo resta da fare alla densità. Qui interessa soprattutto la densità rdell'aria, che ha un ruolo fondamentale nelle forze aerodinamiche. Di per sè la densità viene definita come la quantità di massa contenuta nell'unità di volume, ed ha dimensioni [kg / m³] . È facilmente immaginabile che quanto più l'aria è compressa, tanta più ce ne stà in un metro cubo. La densità dell'aria atmosferica varia quindi in funzione dell'altezza sul livello del mare. Anche in questo caso si trovano tabelle derivate dal sistema pratico che possono provocare confusione, in quanto i valori riportati sono più piccoli di un fattore 9,81. Le formule che li utilizzano, formalmente simili, danno infatti le forze non in Newton ma in kg-peso. A questo occorre fare attenzione.
La tabella riporta i valori di densià dell'aria in funzione della quota sul livello del mare. Si tratta ovviamente di densità media, in quanto i valori sono influenzati dalle condizioni metereologiche, e quindi continuamente variabili. |
Ingresso e cortile di palazzo Lascaris a Torino.
