
Possiamo ora analizzare il programma del DSP, scritto per la realizzazione del sensore solare fine. Le richieste fondamentali che deve soddisfare il processore sono :
a) la comunicazione con i due MACs per l’acquisizione dei dati
b) il calcolo del loro rapporto
c) il filtraggio di tale risultato (FIR passa-basso)
d) l’immediata comunicazione seriale con il PC.Nella figura 1 si può vedere il diagramma di flusso del programma, mentre nell'appendice B.3 ne è riportato il corrispondente codice assembler.

Fig 1 – Diagramma di flusso del programma assemler realizzato per il sensore fine. Per una migliore visione della figura si consiglia di scaricare qui il file .zip + .doc di 17Kb e di stamparlo.
La struttura del programma si basa essenzialmente sulle due routines GET e DSPSERI. La prima viene eseguita quando dalla PAL1 giunge un interrupt e si articola in tre parti, impiegate rispettivamente per la realizzazione dei punti a), b), c). L’ultima istruzione della routine GET si occupa del ricampionamento dei dati, come già spiegato nell’appendice A.1, mandando sulla seriale un quoziente ogni 40 campioni processati.
La routine DSPSERI si occupa della formattazione dei dati e del loro successivo invio alla porta seriale del DSP, tramite il blocco di istruzioni contenuto nella sottoroutine SERIAL, che viene eseguita sotto l’azione dell’interrupt interno XINT, generato dal buffer della seriale (vedi appendice A.4). L’ultima istruzione fa si che i bit uscenti dalla seriale, siano a gruppi di 10, come richiesto dal protocollo della RS-232, ossia uno start bit, gli 8 bit della codifica ascii e lo stop bit.
L’esecuzione di SERIAL è molto più lenta della prima routine, per cui la si è resa interrompibile, per rendere possibile lo svolgimento delle varie operazioni di GET e per evitare quindi la perdita di campioni, indispensabili per un giusto filtraggio. Risulta di fondamentale importanza, alla luce di quanto appena detto, che la routine GET sia eseguita prima dell’arrivo di un altro interrupt esterno o si perderanno uno o più dati.
Quindi si è dovuto trovare l’algoritmo più adatto per eseguire la divisione nel minor tempo possibile e l’implementazione del FIR è stata condotta con il giusto compromesso tra il minor numero di coefficienti e la bontà del filtro.
I coefficienti del FIR, si sono ottenuti con l’ausilio di un opportuno programma (FDAS). Dopo varie prove, la scelta ideale è risultata essere quella ottenuta con una finestratura di tipo Hanning con 201 coefficienti; infatti gli altri tipi di finestratura (rettangolare, triangolare ecc.) a parità di coefficienti non davano un buon risultato.
La tecnica della finestratura, si usa per prendere in considerazione solo una porzione, nel dominio temporale, della risposta impulsiva del filtro. Lo spettro in frequenza del segnale sarà modulato da quello della finestra, per cui la scelta migliore sarebbe quella di una finestra con lo spettro dotato di uno stretto lobo centrale e di bassi lobi laterali (idealmente una d di Dirac), affinché la risposta in frequenza del filtro sia riprodotta il più fedelmente possibile.
La teoria c’insegna [18], per quanto riguarda la finestra rettangolare, che tanto più il lobo centrale è stretto e pronunciato tanto più i lobi laterali saranno alti, per cui una ragionevole scelta sembra essere quella offerta della finestra di Hanning (vedi fig. 4).
Si riporta qui di seguito la risposta in frequenza del filtro utilizzato e le forme delle varie finestre con i loro spettri in frequenza.Fig 2 – Profilo del filtro a 201 coefficienti con frequenza di taglio a 20 Hz, ottenuto con il programma FDAS.
Fig 3 – Forma delle finestre: Hanning (Han), Hamming (Ham), Blackman (Bl), rettangolare (R) e triangolare (T).
Tab 1 – Descrizione matematica delle finestre illustrate nella fig. 2.

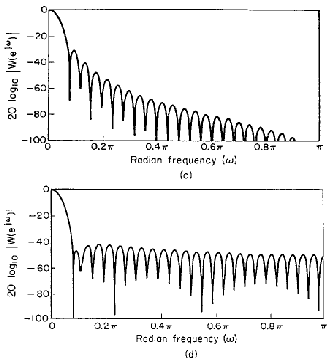
Fig 4 – Spettri in frequenza dei vari tipi di finestre; rettangolare (a), triangolare (b), Hanning (c), Hamming (d), Blackman (e).
Nella prima parte del programma, vengono configurati i vari registri impiegati successivamente nella gestione della seriale e nell’implementazione del FIR; inoltre si creano due buffer in memoria per la costruzione della tabella dei codici ascii e per l’immagazzinamento dei dati già codificati e pronti per essere inviati, al momento opportuno alla porta seriale. Nella figura 5 viene illustrato il metodo della codifica: il dato a 32 bit, acquisito dall’esterno è suddiviso in 8 word da 4 bit (w7-w0), il cui valore numerico (#w) sommato alla locazione di memoria relativa all’inizio del buffer della codifica, punterà al corrispondente valore ascii.
Nella figura ad esempio w4 vale 0010 (210), per cui il suo codice ascii si troverà nella locazione loc_ini+2.
Successivamente il numero codificato verrà scritto nel secondo buffer per poi essere trasferito alla seriale. Applicando il procedimento a tutte le word (w7-w0), si riesce ad inviare alla seriale un numero che il PC interpreterà come il corrispondente a 8 caratteri esadecimali, del dato a 32 bit precedentemente acquisito.
Il buffer dei codici è statico, nel senso che viene riempito una sola volta durante il boot del processore e le sue caselle di memoria non verranno più modificate, ma solo lette, mentre l’altro buffer è dinamico, dal momento che viene aggiornato ogni volta con il valore del nuovo dato acquisito.Fig 5 – Metodo per la codifica ASCII di un dato prodotto.
Per quanto riguarda l’algoritmo della divisione, si è fatto uso di una particolare istruzione, dedicata alla risoluzione di tale operazione. Il comando assembler impiegato è SUBC (Subtrac Intger Conditionally), il quale opera nel modo seguente: consideriamo il caso di un dividendo positivo a 32 bit con i bit significativi e un divisore positivo a 32 bit con j bit significativi; la ripetizione del comando SUBC i-j+1 volte produce un risultato a 32 bit nel quale gli i-j+1 bit meno significativi esprimono il quoziente, mentre i 31-i+j bit più significativi rappresentano il resto. Il divisore (si assume che sia più piccolo del dividendo) viene shiftato a sinistra di i-j posizioni affinché sia allineato con il dividendo; quindi tramite l’istruzione SUBC il divisore shiftato viene sottratto al dividendo e per ogni sottrazione che non produce un risultato negativo, quest’ultimo è sostituito con la differenza, per poi essere shiftata a sinistra di una posizione con l’aggiunta di un 1. Al contrario, se la differenza è negativa, il dividendo è semplicemente shiftato a sinistra di un posto. Tali operazioni, ripetute i-j+1 volte, producono il risultato desiderato. L’algoritmo in questione si applica con la condizione che il divisore sia più piccolo del dividendo, ma continua ad essere valido anche nel caso contrario con delle opportune modifiche; infatti, se vogliamo k numeri significativi dopo la virgola, bisognerà shiftare il dividendo di k posizioni a sinistra, prima di poter applicare la normale procedura con i sostituito da i+k. Chiaramente dovrà risultare: i+k<32. Nel caso in questione, l’algoritmo esposto poc’anzi è stato applicato per ricavare la parte intera del quoziente, mentre per quella frazionaria (una cifra significativa in base 16 dopo la virgola) non è stato applicabile dal momento che la disuguaglianza i+k<32 poteva essere non soddisfatta; in sua sostituzione è stata scritta una routine che shifta di un posto a sinistra il resto e calcola quante volte vi è contenuto il dividendo. Nel riquadro alla pagina seguente viene illustrata l’azione del comando SUBC.
Home | Precedente | Successivo