

Il filtro di ingresso
Come abbiamo visto, se un segnale viene campionato rispettando la condizione di Nyquist si è certi che il contenuto informativo ditale segnale non viene perso. Occorre però che sia rispettata anche la condizione relativa alla limitazione della banda del segnale da campionare. In genere i segnali non presentano una banda limitata (anche se le armoniche di frequenza superiore a un valore, proprio di ciascun segnale, possono essere trascurate) e ciò impone il filtraggio a una fMAX opportunamente valutata caso per caso. Inoltre è sempre necessario assicurarsi che lo spettro del segnale da campionare non contenga armoniche (o che a tale spettro non si sovrappongano armoniche spurie, per esempio dovute a rumori ad alta frequenza) aventi frequenze superiori alla frequenza desiderata. Per queste ragioni il segnale da campionare viene normalmente filtrato mediante un filtro passa-basso che garantisca: Da quanto detto si comprende che l'ingresso del blocco di campionamento è costituito da un filtro passa-basso.
L’effettiva limitazione della banda del segnale al valore coretto di fMAX.
L’eliminazione di armoniche di frequenza superiore a fMAX.
Per esempio durante la fase di registrazione prima della sua conversione in forma digitale e successiva incisione su Compact Disk, il segnale audio viene filtrato mediante una sezione passa basso di ordine opportuno e con frequenza di taglio inferiore a 20 kHz.
Da quanto detto si comprende che l’ingresso del blocco di campionamento è costituito da un filtro passa basso.
Per comprendere correttamente le problematiche relative al campionamento (comunque senza la pretesa di considerarne la trattazione matematica) è necessario, però, anticipare il problema della ricostruzione del segnale campionato. Tale problema, infatti, è strettamente connesso a quello del campionamento. Il teorema del campionamento, formulato secondo l'espressione fC³2fMAX , è comprensibile e definibile considerando proprio l'aspetto della ricostruzione del segnale.
La ricostruzione del segnale
Normalmente un segnale viene campionato non solo allo scopo di essere convertito in forma digitale, e come tale elaborato, ma anche al fine di poter essere successivamente riportato in forma analogica e in questa forma utilizzato. Si pensi ancora al segnale audio inciso digitalmente su CD. L'elaborazione digitale del segnale audio consente non solo l'eliminazione dei disturbi tipici della registrazione analogica ma anche la sovrapposizione al segnale originale di "effetti" particolari, quali il riverbero, l'eco, la compressione e altri ancora (rendendo possibile anche la correzione di situazioni imbarazzanti che in un’esecuzione "dal vivo" non sarebbero tollerabili: per esempio, una voce mediocre o un percussionista con difficoltà a "tenere il tempo" che può essere comodamente sostituito da suoni percussivi generati digitalmente e perfettamente temporizzati). Il segnale così elaborato deve poi essere riascoltato. Il lettore di CD svolge questa operazione: convertire in forma analogica il segnale digitale. L'operazione che consente di ottenere da un segnale in forma digitale il corrispondente segnale analogico viene chiamata ricostruzione del segnale.

Fig. 5 a) Spettro V(f) del segnale V a banda limitata b) Spettro Vc(f) del segnale Vc campionato
Per comprendere come sia possibile realizzare questa operazione consideriamo la figura 5. Tale figura riporta un possibile andamento dello spettro V(f) di un segnale analogico in tensione v e il corrispondente andamento in frequenza dello spettro VC(f) del segnale campionato vC. Il segnale v presenta una banda limitata di larghezza fMAX Campionando un segnale a banda limitata si ottiene il segnale campionato vC il cui spettro presenta particolari proprietà. Tali proprietà sono tipiche di ogni segnale campionato (a parte ovviamente lo specifico andamento in frequenza che dipende da quello del segnale analogico v e che nel caso in esame è triangolare).
Lo spettro di ogni segnale campionato ottenuto da un segnale a banda limitata è sempre costituito da:
Lo spettro del segnale analogico sorgente (di larghezza fMAX ).
Altri spettri laterali di larghezza 2 fMAX centrate intorno a frequenze multiple della frequenza di campionamento fC (2fC, 3fC così via).
La figura 5 illustra le suddette caratteristiche riferite alla tensione analogica v e al corrispondente segnale campionato vc
Da quanto detto si deduce che il segnale campionato, il cui andamento temporale ricordiamolo deve essere come quello di figura 2b, è costituito da uno spettro decisamente diverso da quello del segnale sorgente e quindi, come è evidente, anche il suo andamento temporale è differente da quello del segnale sorgente. La caratteristica struttura spettrale di VC(f), però, consente di riottenere (cioè di ricostruire) il segnale analogico sorgente intervenendo sullo spettro del segnale campionato. È sufficiente, infatti, filtrare il segnale campionato mediante un passa basso (chiamato filtro di ricostruzione) la cui risposta in frequenza presenti le seguenti caratteristiche:
L'andamento del modulo sia costante (piatto) fino a fMAX e poi decada con pendenza adeguata in modo da annullarsi in corrispondenza di una frequenza fN minore o uguale a (fC- fMAX), cioè fN £ fC - fMAX
L'andamento della fase sia lineare in modo da non introdurre distorsioni di fase nel segnale ricostruito.
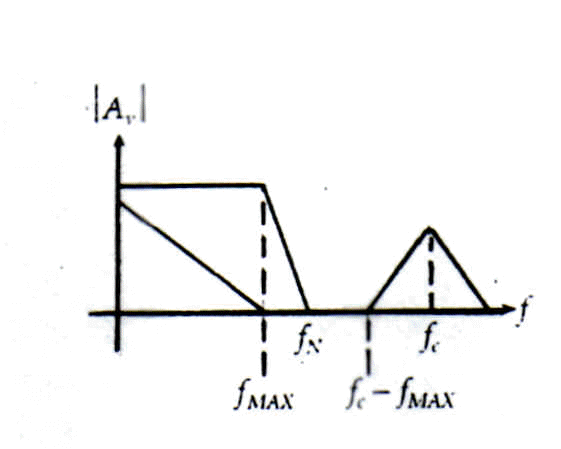
Fig. 6 Caratteristica del modulo passa basso necessaria per la ricostruzione del segnale
La figura 6 illustra in colore l'andamento che il modulo del passa basso deve assumere per garantire la ricostruzione del segnale. Tale andamento è sovrapposto a quello dello spettro del segnale campionato. Un passa basso la cui risposta in frequenza del modulo abbia l'andamento indicato elimina alla sua uscita gli spettri del segnale campionato centrati intorno ai multipli di fC, consentendo di apparire in uscita solo allo spettro del segnale sorgente. L'uscita del filtro, pertanto, è il segnale analogico originale.
Supponendo che il filtro sia ideale (cioè che il suo roll - off sia infinito) la. frequenza fN coincide con fMAX e quindi, considerando quanto sopra stabilito, deve risultare:
fC - fMAX ³ fMAX
da cui si ricava:
fC ³ 2fMAX
Questa relazione è esattamente l'equazione di Shannon e ciò spiega la relazione esistente tra il campionamento di un segnale analogico e il problema della sua ricostruzione. Considerando ancora la figura 6 si osserva che la condizione fC=2fMAX è puramente teorica, perché essa darebbe origine a un segnale campionato avente uno spettro come quello di figura 7.
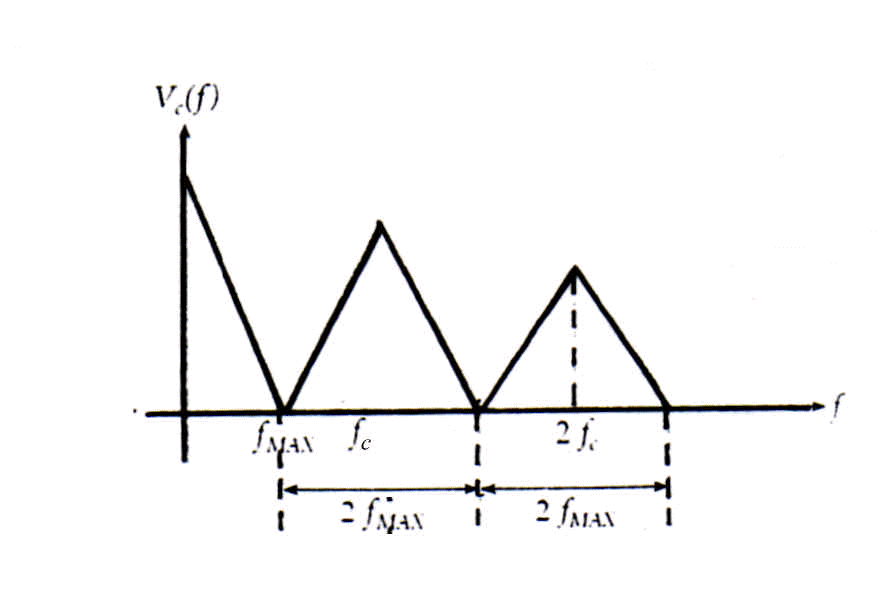
Fig. 7 Spettro armonico di un segnale campionato con fC=2fMAX
Per ricostruire da tale spettro l'originale segnale analogico occorrerebbe un filtro con roll-off infinito, cioè un filtro ideale impossibile da realizzare. Nelle applicazioni reali, quindi, la condizione di Shannon viene applicata imponendo che fC sia maggiore di 2fMAX. Ciò garantisce l'esistenza di un intervallo tra fMAX e (fC - fMAX) che consente di realizzare un passa basso con pendenza non infinita la cui risposta in ampiezza può effettivamente annullarsi alla frequenza fN£ fC -fMAX
Il fenomeno dell'aliasing
Se il campionamento viene effettuato in disaccordo con l'equazione Shannon, vale a dire se fC³2fMAX allora tale campionamento è scorretto e lo spettro del segnale campionato si modifica in modo tale che gli spettri laterali si sovrappongono l'uno con l'altro e in particolare con quello del segnale sorgente. La figura 8 descrive un possibile esempio ditale sovrapposizione (per chiarezza la figura illustra il caso in cui solo il primo spettro laterale si sovrappone a quello del segnale sorgente). Nello spettro del segnale sorgente, quindi, risulta incluso un insieme di armoniche che in realtà non appartengono al suddetto segnale sorgente. Lo spettro di tale segnale, pertanto, risulta alterato e ciò provoca la distorsione del segnale stesso (il cui andamento temporale può risultare anche fortemente diverso da quello originale). Questa interferenza spettrale che distorce il segnale sorgente viene chiamata aliasing. Il fenomeno dell'aliasing impedisce la corretta ricostruzione del segnale sorgente qualunque sia il roll off del filtro di ricostruzione.
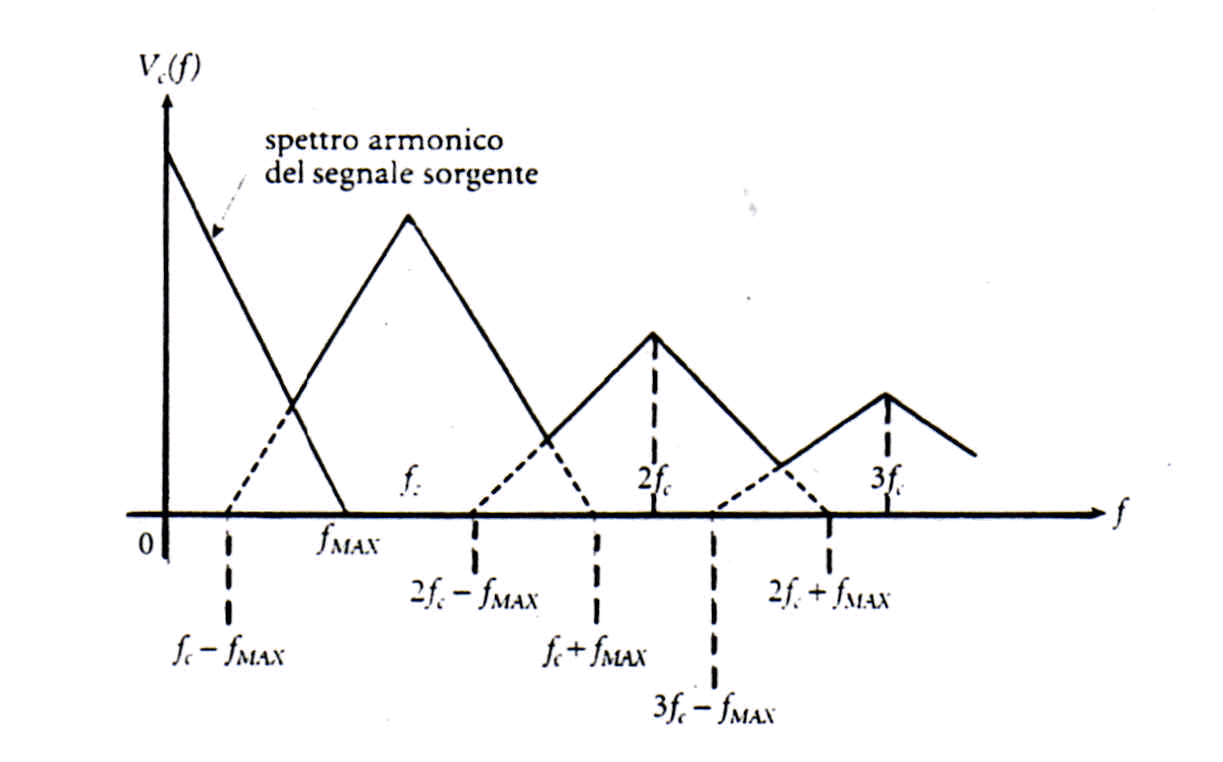
Fig. 8 Esempio di spettro con aliasing
In termini più completi occorre riconoscere che l'aliasing si verifica ogni qualvolta lo spettro armonico del segnale sorgente viene modificato dalla presenza di armoniche estranee allo spettro stesso le quali, per cause diversificate, vengono riportate (folded back) all'interno dello spettro del segnale sorgente. Per esempio, l'insorgenza dell'aliasing, oltre che dalla sovrapposizione spettrale generata da una insufficiente frequenza di campionamento fC, è provocata anche da altre cause, quali le caratteristiche funzionali del modulo campionatore e del DAC. In ogni caso l'aliasing deve essere evitato. Il principale criterio utile a questo scopo è la scelta della corretta frequenza di campionamento in relazione alle caratteristiche del segnale da campionare, cioè il rispetto della condizione di Shannon.
Considerazioni sul filtro d’ingresso
Ripensando al fenomeno dell'aliasing è opportuno formulare, seppur brevemente, alcune considerazioni sul filtro di ingresso. Questo filtro, infatti, viene spesso chiamato filtro anti aliasing. Affinché il filtro d’ingresso garantisca l'effettiva limitazione a fMAX della larghezza di banda del segnale di ingresso, così da rendere possibile la corretta valutazione di fC in base alla condizione di Shannon, occorre che la sua risposta in ampiezza sia come quella di figura 9, cioè ideale.
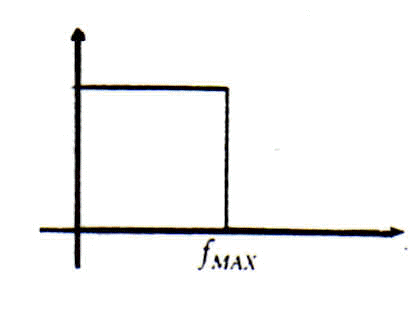
Fig. 9 Risposta in ampiezza ideale del filtro d'ingresso anti aliasing
Un filtro di questo genere non introduce attenuazioni in banda e, presentando un roll-off infinito, limita esattamente a fMAX la larghezza di banda dell'ingresso. In questo modo è possibile eliminare l'aliasing (da cui la definizione di filtro anti aliasing) grazie a una esatta valutazione della frequenza di campionamento. Un filtro del genere, però, non esiste. Praticamente, infatti, i filtri che si possono realizzare presentano:
Attenuazione in banda e quindi possibili distorsioni d’ampiezza;
Andamenti non perfettamente lineari della fase e conseguenti distorsioni di fase;
Roll off elevato ma comunque finito. Ciò consente il passaggio d’armoniche di frequenza superiore a fMAX seppure con ampiezza attenuata e conseguente distorsione del segnale da campionare dovuta alla presenza di armoniche spurie (aliasing).
Nella fase implementativa, quindi, occorre ricercare per il filtro anti aliasing una soluzione in grado di conciliare le esigenze teoriche con quelle effettivamente realizzabili. In genere si tendono ad adottare filtri Butterworth, le cui prestazioni migliorano al crescere dell'ordine del filtro, oppure, al fine di minimizzare l'ingombro circuitale, filtri integrati a capacità commutata. Queste indicazioni non escludono scelte diverse che vengono operate in relazione alla natura del segnale da campionare e della applicazione specifica.