Immaginiamo che i due numeri primi di Alice siano: p=47 e q=61.

Con E=1183, la chiave pubblica è la funzione:

mentre la chiave privata è la funzione:

(vedi fine paragrafo 5)

Bob ha intenzione di trasmettere segretamente ad Alice la frase: Sono uscito.

Siccome le funzioni modulari esponenziali sono ed agiscono, su numeri naturali, Bob allora converte la sua frase in un numero P, mediante ad esempio la successiva tabella degli alfabeti, in cui l'alfabeto ordinario è messo in corrispondenza con un alfabeto numerico:

La versione numerica della frase: Sono uscito, sarà dunque: P=4414131462201802081914.

A questo punto Bob effettua il frazionamento del numero P in una successione Pi di blocchi di numeri, tutti con lo stesso numero di cifre, ad esempio 3 cifre, ottenendo:

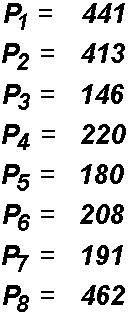
Si noti l'aggiunta del numero 62 (lo spazio bianco) in coda a P, per fare in modo che anche l'ottavo blocco Pi contenga 3 cifre.

Finalmente Bob può dar luogo alla cifratura vera e propria. Determina cioè gli 8 blocchi cifrati Ci, utilizzando la funzione C, dopodichè li trasmette ad Alice.

Per il primo blocco Ci è:

come si è già visto nel paragrafo 2.

Con procedura identica per gli altri blocchi sarà:

Vediamo adesso gli adempimenti di Alice.

Ricevuti gli 8 blocchi Ci, semplicemente utilizzando la funzione P, solo e soltanto Alice, sarà in grado di ricavare gli 8 blocchi Pi.

Se qualche blocco Pi ha un numero di cifre inferiore a 3, Alice aggiunge degli 0 a sinistra, quindi accorpa i vari Pi così determinando P.

Utilizzando infine la tabella degli alfabeti, deconverte P, risalendo infine alla frase: Sono uscito.