Vediamo qualche esempio:
- N(9)=6 (ovvero i numeri: 1, 2, 4, 5, 7 e 8)
- N(12)=4 (ovvero i numeri: 1, 5, 7 e 11)
- N(18)=6 (ovvero i numeri: 1, 5, 7, 11, 13 e 17).

Se m è un numero primo, naturalmente è: N(m)=m-1.

Notevole è la proprietà:

- se m è pari al prodotto di due numeri primi, diciamo p e q, è:

Vediamo qualche esempio:
- N(6)=N(2*3)=(2-1)(3-1)=1*2=2 (ovvero i numeri: 1 e 5)
- N(10)=N(2*5)=(2-1)(5-1)=1*4=4 (ovvero i numeri: 1, 3, 7 e 9 )
- N(30)=N(2*3*5)=(2-1)(3-1)(5-1)=1*2*4=8 (ovvero i numeri: 1, 7, 11, 13, 17, 19, 23 e 29).

Come vedremo, l'importanza del funzione di Eulero N(m) nell'ambito della crittografia a chiave pubblica, sta proprio nella semplicità con cui è possibile determinarla, anche quando m è il prodotto di due numeri primi molto grandi.

La struttura di una funzione modulare esponenziale è la seguente:

come prima:
- E ed m sono delle costanti numeriche
- C è la variabile dipendente
- P è la variabile indipendente.

Come prima C è un resto, e dato che pensiamo di dover far ricorso alla funzione modulare esponenziale inversa, in cui è P ad essere la variabile dipendente, anche P è un resto.

E allora C e P sono due numeri naturali (0, 1, 2, 3, .....), con valori compresi fra 0 ed (m-1).

Ora però la funzione:

è invertibile solo se E ed N(m) sono primi fra loro, ovvero solo se E ed N(m) non hanno alcun fattore in comune.

Con riferimento intanto alla notazione X(mod m)=R, con D pari a una costante, è:

E' infatti:

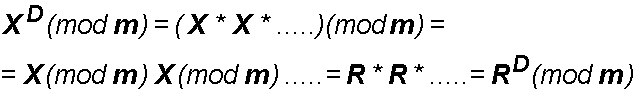
Se infine facciamo riferimento ad un teorema della Teoria dei numeri, ovvero a quello espresso in formula qui di seguito:

possiamo finalmente invertire la nostra funzione modulare esponenziale.

Essendo dunque:

è anche:

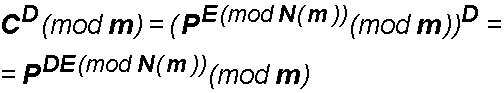
Basta dunque cercare una D tale che: DE(mod N(m))=1, perchè così la nostra funzione inversa vale:

E'importante sottolineare che D esiste solo se E ed N(m) sono primi fra loro.

Vediamo un esempio.

Intanto per rendere facilmente determinabile N(m), consideriamo m come prodotto dei due numeri primi 47 e 61, in tal modo è
N(m)=N(2867)=46*60=2760.

Essendo 2760=3*5*8*23, scegliamo E, che deve essere primo con 2760, ad esempio come risultato del prodotto: 7*13*13, e quindi è E=1183.

La funzione modulare esponenziale che dobbiamo dunque invertire è :

Per poterla effettivamente invertire, dobbiamo cercare una D tale che: 1183D(mod 2760)=1.

Ebbene, l'algoritmo del precedente paragrafo 4, dopo aver sostituito m con N(m), si arresta dopo sole 3 iterazioni (QUOZ=3), fornendoci il risultato: D=7, come può essere facilmente verificato.

La cercata funzione modulare esponenziale inversa è dunque: