Studio dell'assetto di motoveicoli da competizione in entrata ed in
uscita dalle curve.
di Giovanni Chinaglia
Premesse
La messa a punto di una moto da
competizione richiede l'esecuzione di lunghi e costosi test in pista durante i
quali, mediante la telemetria, vengono registrate ed analizzate svariate
grandezze relative sia alla"ciclistica" e sia al motore.
Per diminuire il
numero di prove in pista è importante avere a disposizione uno strumento
numerico che consenta di studiare l'influenza dei singoli parametri sull'assetto
assunto dal veicolo in entrata ed in uscita dalle curve. In questo lavoro
preliminare si mostra come sia possibile studiare il comportamento del veicolo,
in entrata ed in uscita dalle curve, al variare di alcuni parametri tipici delle
sospensioni quali precarico, smorzamento in compressione ed in
estensione.
Definiamo dapprima che cosa si intende per
assetto :
Tale configurazione viene determinata nella fase di progetto
del motociclo, quando vengono decisi il passo, l'avancorsa, l'inclinazione del
cannotto di sterzo, i diametri delle ruote, la lunghezza e l'inclinazione
iniziale del forcellone e la posizione del perno dello stesso rispetto al perno
pignone.
Si deve notare che il passo effettivo della moto varia al variare
dell'affondamento delle sospensioni (perché la ruota anteriore è vincolata a
muoversi lungo un asse inclinato sulla verticale e quella posteriore su di un
arco di circonferenza con centro nel perno pignone); per gli stessi motivi
variano anche l'inclinazione dello sterzo e l'avancorsa.
In genere l'assetto
si riferisce al moto di beccheggio e allo spostamento vericale della "massa
sospesa" . Con il nome di "massa sospesa" viene definita la massa che viene
appunto sostenuta dalle sospensioni: in sostanza il telaio , il pilota, il
serbatoio, il manubrio, parte delle forcella.
L'assetto ovviamente dipende
dalle caratteristiche di rigidezza e di smorzamento delle
sospensioni.
Importante oltre lo studio assetto è anche lo studio delle
condizioni di aderenza ossia dell'andamento temporale dei carichi sulle ruote.
In alcuni casi i carichi possono ridursi notevolmente e possono presentare delle
fluttuazioni che possono innescare saltellamenti delle ruote e consumi
irregolari dei pneumatici.
Lo studio
Lo studio viene svolto su di una particolare schematizzazione
bidimensionale del motoveicolo, chiamata "modello piano" e rappresentata in
figura 1:
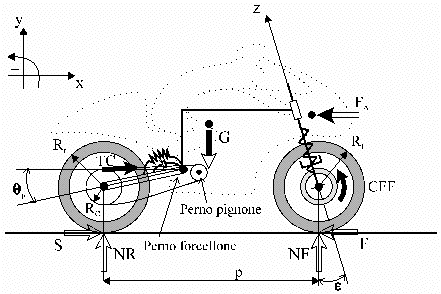
Figura 1 Modello piano del motoveicolo con le forze che agiscono su di esso.
Le forze che agiscono sul veicolo possono essere classificate in :
forze che determinano il moto: TC (Tiro Catena) e
CFF (Coppia Frenante Frontale);
| forze di contatto pneumatico-strada: NR ed
NF (rispettivamente reazione verticale posteriore e reazione verticale
anteriore esplicate dai pneumatici), S e F (rispettivamente
azioni di spinta e di frenata che si realizzano a livello strada come
conseguenza del tiro catena o della coppia frenante);
| forza di resistenza aerodinamica: FA,
modellata secondo la relazione
|
dove Cd = coefficiente di drag; forza peso G. | |
Il modello è provvisto di sospensioni, realizzate
mediante una molla ed uno smorzatore disposti in parallelo ; lo smorzatore
è di tipo a doppio effetto, cioè è in grado di realizzare differenti
coefficienti di smorzamento per le fasi di estensione e di compressione.
Per
svincolarsi dal cinematismo utilizzato al retrotreno, la sospensione posteriore
è realizzata mediante molla e smorzatore di tipo torsionale avente opportune
caratteristiche, applicati direttamente al perno forcellone.
La cinematica e
la dinamica dei corpi che compongono il modello sono gestite da un apposito
programma scritto in linguaggio Fortran, sviluppato in modo da ricevere in
ingresso le dimensioni caratteristiche di una reale moto da competizione (si
tratta di una Aprilia 250 RSV).
Grazie a tale software vengono svolte delle
simulazioni dinamiche su di un tratto di pista del Mugello (figura 6),
relativamente al quale vengono ricavati - da simulazioni sul metodo della
"manovra ottima" - gli andamenti nel tempo delle grandezze che determinano la
dinamica del motoveicolo, che sono:
| tiro catena TC : |
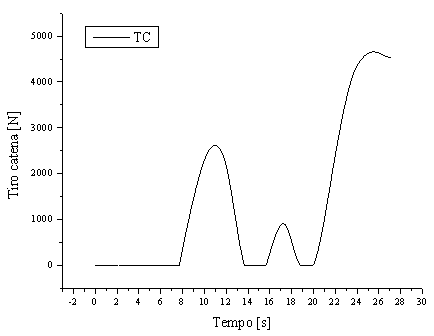
Figura 2 Andamento nel tempo del tiro catena.
| coppia frenante frontale CFF: |
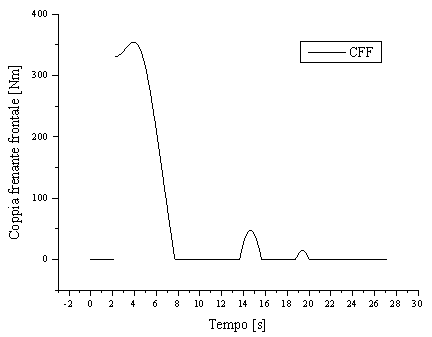
Figura 3 Andamento nel tempo della coppia frenante anteriore impartita al modello piano.
| effetto delle curve g*: il modello piano infatti non è provvisto della terza dimensione necessaria a percorrere delle traiettorie curvilinee, ma è possibile imporgli lo schiacciamento che la moto subisce nel proprio piano longitudinale durante la percorrenza delle curve. |
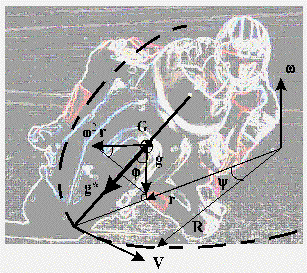
Figura 4
La curva viene simulata mediante il parametro definito
"accelerazione di gravità apparente' - g* - che va a sostituire
l'accelerazione reale - g - nell'elaborazione matematica delle
equazioni del moto.
L'accelerazione apparente viene calcolata come somma
della componente dell'accelerazione di gravità reale e della componente
dell'accelerazione centrifuga lungo l'asse della moto ; è quindi
funzione dell'angolo di rollio, della velocità di imbardata e della
velocità di avanzamento. Infatti quando la moto percorre una curva si
piega dell'angolo di rollio f e ruota attorno al centro di istantanea
rotazione dell'angolo y (imbardata) ; supponendo di identificare il
raggio di curvatura baricentrico con quello relativo al pneumatico, la sua
velocità di imbardata y ' è istantaneamente uguale alla velocità angolare w
del motoveicolo nel suo moto di rotazione attorno al centro di istantanea
rotazione, ma dato che istantaneamente la traiettoria percorsa è circolare, la
velocità angolare w è anche pari al rapporto tra velocità di avanzamento e
raggio di curvatura. Tutto ciò permette di esprimere l'accelerazione
centrifuga come prodotto di velocità di avanzamento e velocità di
imbardata.
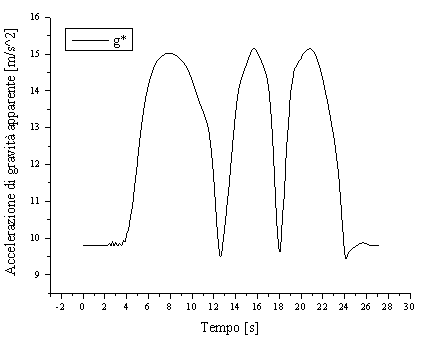
Figura 5 Andamento nel tempo dell'accelerazione apparente di gravità impartita al modello piano.
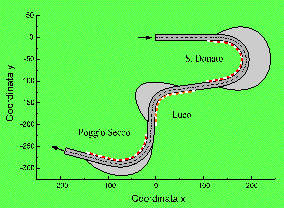
Figura 6 Tratto di pista oggetto delle simulazioni.
Come risultato dell'elaborazione si ottiene l'andamento temporale delle stesse grandezze rilevate mediante la telemetria(come l'affondamento delle sospensioni ) e sia grandezze proprie della modellazione matematica - come le reazioni verticali esplicate dai pneumatici.
I risultati
In virtù di quanto appena detto è possibile confrontare
l'affondamento delle sospensioni ricavato dalle simulazioni con quello ottenuto
da un reale sistema di telemetria, relativamente allo stesso tratto di
circuito:
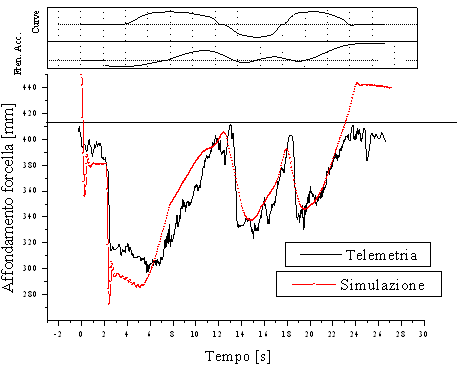
Figura 7 Confronto tra l'affondamento della sospensione anteriore ottenuto dalla simulazione e quello ottenuto dalla telemetria su pista.
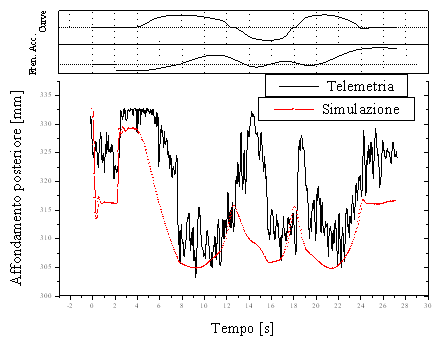
Figura 8 Confronto tra l'affondamento della sospensione posteriore ottenuto dalla simulazione e quello ottenuto dalla telemetria su pista.
Il codice di calcolo così approntato permette di trarre una serie di conclusioni, tra le quali le più rilevanti sono:
| effetti del precarico delle molle: |
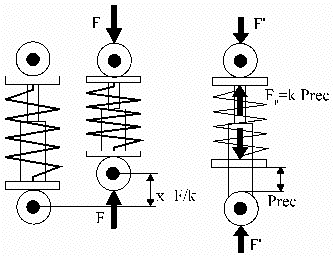
figura 9
osservando gli andamenti dell'affondamento della sospensione anteriore con e senza precarico (figura 10), si può notare come le due curve risultino perfettamente corrispondenti tra loro, ma traslate l'una rispetto all'altra di una certa quantità (37 mm nell'esempio) in quanto partono da due diverse posizioni di equilibrio - ogni curva infatti comprende un transitorio iniziale in cui la moto si assesta sotto il proprio peso e raggiunge una posizione di equilibrio.
Tale traslazione ha origine dal fatto che, osservando lo schema di figura 9, quando viene impartito precarico ad una sospensione, che non sia già completamente estesa, essa non si comprimerà fino a quando la forza che le viene applicata non superi il valore del precarico.
Parte della forza peso viene così assorbita dal precarico.
Figura 10 Affondamento forcella con e senza precarico.
Come conseguenza del precarico alla sospensione anteriore si ha che l'avantreno risulta più scarico nelle fasi di accelerazione in uscita di curva (figura 11).
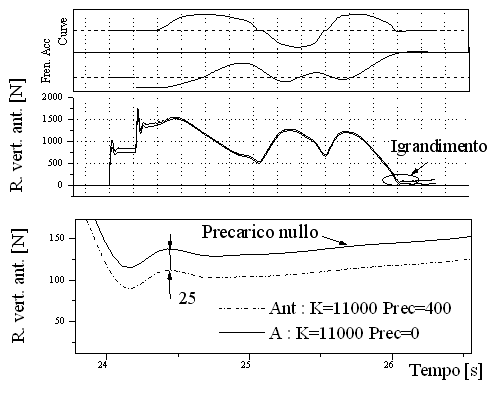
Figura 11 Andamento della reazione verticale anteriore con e senza precarico.
Come conseguenza del precarico alla sospensione posteriore si ha, invece, che il retrotreno rimane più scaricato nelle fasi di frenata che precedono gli ingressi in curva (figura 12).
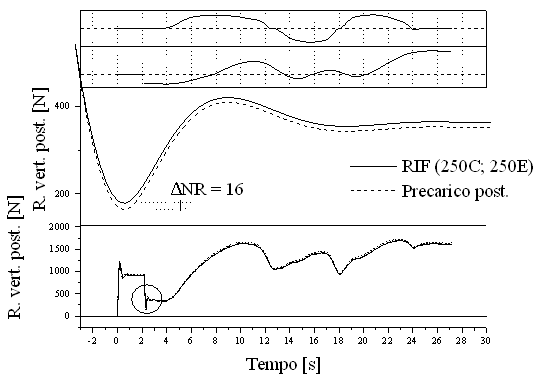
Figura 12 Andamento della reazione verticale posteriore con e senza precarico;
| effetti delle regolazioni sugli
smorzamenti: la figura 13 evidenzia quanto sia importante mantenere costante un livello medio di smorzamento, cioè se p.e. si diminuisce lo smorzamento nella fase di compressione deve essere aumentato proporzionalmente lo smorzamento in estensione, di modo che rimanga costante la somma degli smorzamenti nelle due fasi; agendo diversamente si va a diminuire la quantità di energia che viene dissipata dallo smorzatore, e l'oscillazione risulta più prolungata nel tempo. |
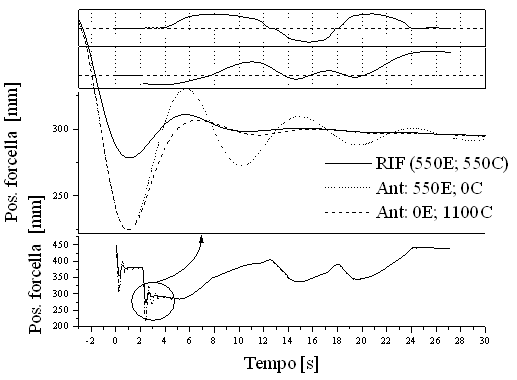
Figura 13 Affondamento della forcella mantenendo un livello costante di smorzamento e non.
E' interessante notare che è stata rilevata una distribuzione ottimale dello smorzamento, al retrotreno, tra le fasi di estensione e di compressione, relativamente alla frenata: la figura 14 permette di evidenziare che tale distribuzione ottimale è a favore dell'estensione (in rapporto 4/1 o 3/2), mentre una distribuzione dello smorzamento a favore della compressione (in rapporto 4/1) scarica il retrotreno di ben 106 N (» 10 Kg).
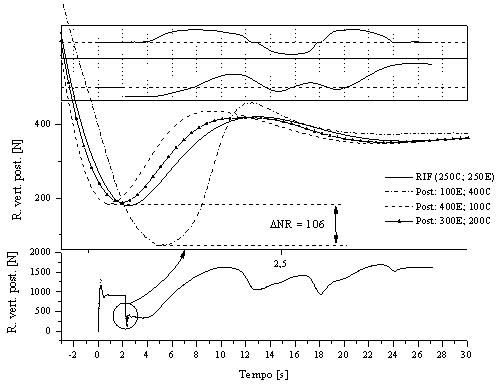
Figura 14 Reazione verticale posteriore, nella frenata, per diverse distribuzioni dello smorzamento nella sospensione posteriore;
| variazione di un parametro geometrico,
la posizione del perno pignone: in base allo schema di figura 15 le forze che agiscono sul retrotreno determinano, sul forcellone, un momento che tende ad estendere la sospensione posteriore. |
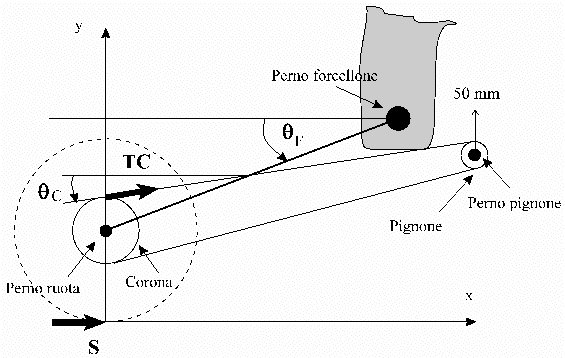
figura 15
Spostando verso l'alto (di 50 mm) la posizione del perno pignone diminuisce l'entità di questo effetto anti-affondamento, conseguentemente la sospensione posteriore affonda di più nelle fasi di accelerazione.
La modifica apportata implica un'altra importante conseguenza: la figura 16 dimostra che, nella nuova configurazione, l'avantreno rimanere più caricato (18 N nell'esempio) durante le fasi di accelerazione in uscita di curva.
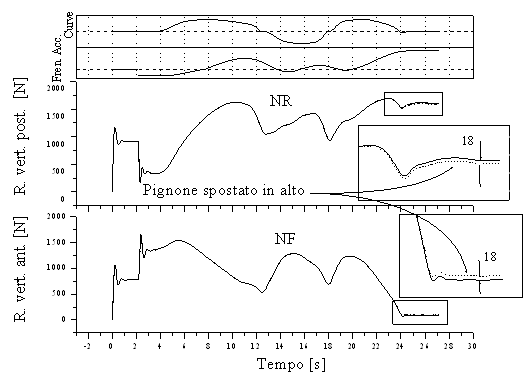
Figura 16 Reazioni verticali anteriore e posteriore, prima e dopo la modifica alla posizione del perno pignone.