MANOVRABILITÀ E MANEGGEVOLEZZA DI MOTOCICLETTE DA COMPETIZIONE SU TRATTI DI CIRCUITO REALE   F. Biral & M. Da Lio Dipartimento di Ingegneria Meccanica, Università di Padova, Italia

	Introduzione
	Maneggevolezza e Manovrabilità
	Manovra ottima
	Handling
	Esempi
	Conclusioni

 

Queste ricerche sono svolte in collaborazione con la squadra corse Aprilia e in particolare con l'ing. Luca Fabbri.

Introduzione Lo studio della dinamica dei motocicli è un problema piuttosto difficoltoso da trattare, per la complessità della descrizione matematica e perché si tratta di veicoli tendenzialmente instabili. Infatti, senza controllo cadrebbero di lato a causa del modo di capsize. Sarebbe molto utile ai progettisti conoscere in fase di progettazione come variano le prestazioni di un motociclo su tratti reali di pista in funzione dei principali parametri costruttivi. Inoltre sarebbe importante quantificare le prestazioni indipendentemente dalla abilità del pilota, ma in riferimento alle sole caratteristiche intrinseche del mezzo. Con questo obbiettivo è stato sviluppato un metodo, detto della manovra ottima, e un software (chiamato Handling) che è in grado di quantificare la maneggevolezza e la manovrabilità di un motociclo su tratti stradali realistici, a prescindere dal pilota e al variare delle principali caratteristiche del veicolo. indice Manovrabilità e Maneggevolezza I concetti di manovrabilità e di maneggevolezza, sebbene di ampio uso, non hanno ancora una definizione rigorosa e univoca. Pertanto occorre chiarire innanzittutto il significato che è attribuito loro in questo documento. Si definisce maneggevole un veicolo che risulta facile da guidare. Questo richiede il giudizio di un pilota che può riconoscere veicoli differenti come più o meno facili da guidare. Al contrario si definisce manovrabile un veicolo in grado di eseguire velocemente manovre complesse. Questo corrisponde alla capacità di completare una certa manovra il più in fretta possibile e nel rispetto dei soli limiti fisici (ad esempio senza superare l'aderenza dei pneumatici o i bordi della strada) ma senza considerare lo sforzo fisico e mentale del pilota. Per manovra si intende un generico moto da una posizione iniziale assegnata ad un'altra finale pure assegnata e restando nei limiti di una striscia che rappresenta il tracciato. A differenza della della maneggevolezza, la manovrabilità è dunque definita indipendentemente dalla abilità del pilota ed è pertanto un indice intrinseco delle prestazioni di un veicolo. Con parole più semplici la manovrabilità è una caratteristica "naturale" esclusiva del veicolo, molto importante per definire le qualità dinamiche da questo possedute, e in pratica in grado di dire se il veicolo in questione è intrinsecamente migliore rispetto ad un altro preso a confronto, a prescindere dal pilota. Dalle definizioni date risulta evidente che una buona manovrabilità del veicolo è condizione necessaria ma non sufficiente per avere anche una buona maneggevolezza. Dal punto di vista rigoroso matematico, sia manovrabilità che maneggevolezza possono essere quantificate per mezzo di una funzione penalità, definita come un integrale nell'intervallo temporale T nel quale la manovra assegnata viene eseguita:   La funzione integranda dipende dallo stato x e dagli ingressi u ed è opportunamente formulata in modo da richiedere una velocità di percorrenza il più possibile elevata e al tempo stesso in modo da penalizzare stati del veicolo che siano prossimi ai limiti fisici (di aderenza, bordo strada ecc). Qualora nella funzione integranda fossero anche presenti dei termini aggiuntivi che rispecchiano un costo di attuazione da parte del pilota si avrebbe invece una misura di maneggevolezza. indice Metodo della manovra ottima Per calcolare la manovrabilità, come integrale sopra definito, occorre prima determinare il moto del veicolo fra gli stati iniziali e finali. Esistono infinite soluzioni ovviamente, che matematicamente corrispondono alla possibilità di assegnare differenti ingressi u e che fisicamente corrispondono a differenti traiettorie percorse dal motociclo per raggiungere la posizione finale. Fra tutte le soluzioni si sceglie evidentemente quella più efficiente, ovvero quella che è caratterizzata dal minimo valore dell'indice integrale I sopra definito. Questo rappresenta il migliore risultato che il veicolo dato può conseguire nell'eseguire la manovra assegnata. Il minimo valore dell'indice I che un dato veicolo può conseguire in una data manovra ne quantifica quindi la manovrabilità, e risulta diverso da veicolo a veicolo. E come se si avesse a disposizione un pilota perfetto, o ideale, che sceglie sempre la migliore tra tutte le possibili traiettorie (la manovra ottima) in modo da percorrere il tratto di circuito assegnato sfruttando al massimo le caratteristiche dinamiche del motociclo la pista a disposizione. indice Il programma di simulazione handling E' stato realizzato un software di simulazione, denominato handling, che risolve il problema della manovra ottima (matematicamente si tratta di un problema di controllo ottimo fra stati iniziali e finali assegnati) e consente quindi di quantificare la manovrabiltà note le caratteristiche del veicolo. Il software è basato su un modello matematico semplificato del veicolo che ne descrive accuratamente solo il moto in grande. Nonostante ciò richiede l'integrazione di un sistema di 27 equazioni differenziali con condizioni al contorno (gli stati iniziali e finali). La traiettoria da eseguire può essere vincolata a restare entro una striscia definibile a piacere in modo da rappresentare realisticamente un tratto stradale. indice Alcuni risultati I risultati che seguono derivano dalla analisi del comportamento di una motocicletta da competizione reale su un tratto della pista del Mugello: la curva di S. Donato e quella di Luco e Poggio Secco. L'immagine seguente mostra la traiettoria ottimale che è stata individuata con il metodo della manovra ottima e che corrisponde ad una percorrenza con velocità il più elevata possibile. 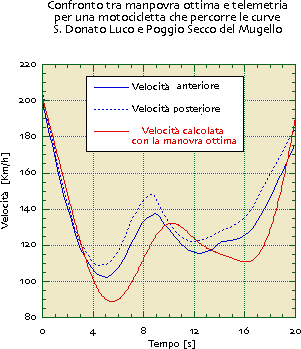Un confronto con i dati telemetrici della velocità è mostrato nella figura seguente. Si vede la velocità calcolata secondo il metodo della manovra ottima e quelle rilevate sulle ruote anteriore e posteriore (sono diverse perché le ruote hanno slip differenti).   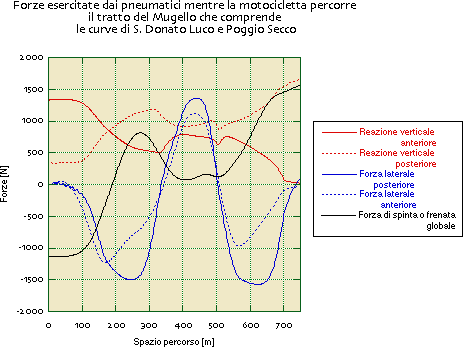L'immagine che segue mostra invece le forze laterali e la spinta sui pneumatici.   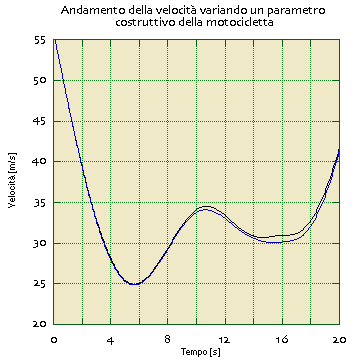Con il software è ovviamente possibile quantificare (come tendenza) l'effetto della modifica di qualcuno dei parametri di progetto. Ad esempio nella figura sottostante si visualizza la differente velocità di percorrenza di due moto differenti (quella con la curva nera è evidentemente più veloce). indice Conclusioni Il metodo della manovra ottima si è dimostrato un'ottimo strumento per quantificare la manovrabilità dei motocicli a prescindere dalla abilità del pilota. I risultati ottenuti sono realistici, nonostante il modello matematico utilizzato sia limitato alla sola dinamica in grande del sistema. Attualmente è in corso di sviluppo un nuovo software di simulazione della manovra ottima basato su un modello matematico del veicolo più dettagliato che comprende più corpi e modelli più sofisticati per i pneumatici. indice