FORZE AGENTI SULLA FORCELLA IN FRENATA
Per poter comprendere nei dettagli il comportamento della motocicletta in frenata è necessario analizzare cosa succede un attimo prima della frenata, cioè quando si chiude la manopola dell’acceleratore e si tira la leva della frizione. Si passa da un moto stazionario o accelerato a un moto decelerato la cui decelerazione è dovuta principalmente all’attrito fra l’aria e la motocicletta. L’istante in cui si passa da una situazione all’altra è raffigurato nella seguente figura.
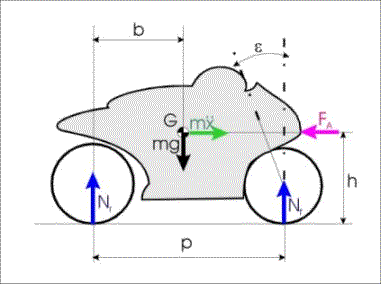
figura 1
dove:
|
Peso della moto +
pilota | |
|
Posizione del baricentro dell’insieme
moto + pilota | |
|
Inerzia del
motociclo | |
|
Forza di resistenza
aerodinamica | |
|
|
Forze scambiate fra i pneumatici e il
piano stradale |
La forza di resistenza aerodinamica è data dalla seguente espressione:
![]()
dove:
|
Densità dell’aria (pari a 1.167
kg/m3 alla pressione atmosferica di 987 mbar e alla temperatura
di 20°C). | |
|
Coefficiente di resistenza
aerodinamica (coefficiente di drag); dipende dalla forma della
motocicletta | |
|
Area della sezione della motocicletta
nella direzione di avanzamento | |
|
Velocità di avanzamento del
veicol |
Si suppone che il centro di spinta del motociclo, nel quale è applicata la forza aerodinamica FA, coincide con il suo baricentro. Il valore del prodotto può variare da 0.25 per motocicli con carenatura e pilota in posizione prona a 0.6 per motocicli privi di carenatura e con pilota in posizione eretta.
Le equazioni cardinali di equilibrio applicate al motociclo nel suo insieme sono:
| Equilibrio delle forze orizzontali | |
| Equilibrio delle forze verticali | |
| Equilibrio dei momenti rispetto al baricentro |
Da queste equazioni è possibile determinare i carichi sulle ruote:
|
Carico sulla ruota
anteriore |
|
|
Carico sulla ruota
posteriore |
I carichi appena determinati possono essere considerati statici perché non sono influenzati dalle condizioni di marcia del veicolo. Infatti non compaiono né la velocità, né l’inerzia del veicolo né la forza di resistenza dell’aria.
Vediamo ora cosa succede quando si azionano i freni. Nel punti di contatto dei pneumatici con l’asfalto si generano delle forze orizzontali come raffigurato nella figura seguente:
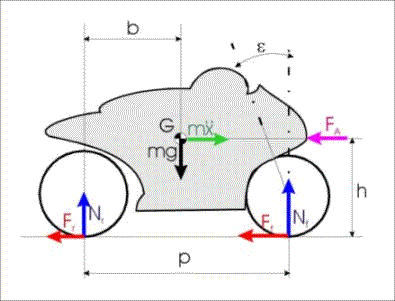
figura 2
In queste condizioni le equazioni cardinali di equilibrio diventano:
|
Equilibrio delle forze
orizzontali |
|
|
Equilibrio delle forze
verticali |
|
|
Equilibrio dei momenti rispetto al
baricentro |
I carichi sulle ruote diventano [1]:
|
Carico dinamico sulla ruota
anteriore |
|
|
Carico dinamico sulla ruota
posteriore |
F è la forza frenante complessiva data dalla somma di Ff e Fr.
In questo caso è lecito parlare di carico dinamico perché Nf e Nr sono funzione anche delle condizioni dinamiche del mezzo che sono inglobate nella F.
Le [1] sono costituite, quindi, da due contributi: uno statico e uno dinamico detto trasferimento di carico e pari a:
![]()
Il trasferimento di carico è proporzionale alla forza di frenata complessiva ed all’altezza del baricentro ed inversamente proporzionale al passo.
Sempre dalle [1] si nota che durante la frenata di ha un aumento del carico sulla ruota anteriore compensato da una uguale diminuzione di carico sulla ruota posteriore. Se si tiene conto del fatto che la forza frenante applicata sul pneumatico è proporzionale al carico dinamico agente sul pneumatico stesso si evince che il contributo maggiore ai fini della frenata arriva proprio dal contatto del pneumatico anteriore con la sede stradale. Questo spiega anche perché l’impianto frenante anteriore è sempre più potente di quello posteriore.
Affinché un pneumatico non slitti durante la frenata, il valore della forza frenante ad esso applicata non deve superare il prodotto del carico dinamico agente sul pneumatico stesso per il relativo coefficiente di aderenza.
Se chiamiamo con ff e fr i coefficienti di aderenza relativi rispettivamente alla ruota anteriore e alla ruota posteriore, la forza frenante complessiva al limite dell’aderenza è data dalla seguente espressione:
![]()
La frenata ottimale si ha quando i coefficienti di attrito fra pneumatico e strada sono uguali per entrambe le ruote; cioè quando:
![]()
In queste condizioni la forza frenante al limite dell’aderenza assume la seguente espressione:
![]()
Da questa equazione si deduce che la massima forza di frenata, rapportata al peso, coincide con il coefficiente di attrito tra le ruote e il piano stradale. Nella tabella sottostante sono riportati alcuni valori del coefficiente di aderenza:
| Asfalto |
|
| Terra battuta |
|
| Cemento |
|
| Asfalto bagnato (1 mm di velo d’acqua) |
|
| Ghiaccio |
|
Nella figura seguente è rappresentato l’andamento dei carichi dinamici rapportati alla forza peso sulle ruote in funzione del coefficiente di aderenza (forza frenante rapportata al peso). Si è supposto che il veicolo abbia il baricentro che cade nella mezzeria del passo e che quindi la ripartizione dei pesi fra le due ruote sia 50% - 50%.
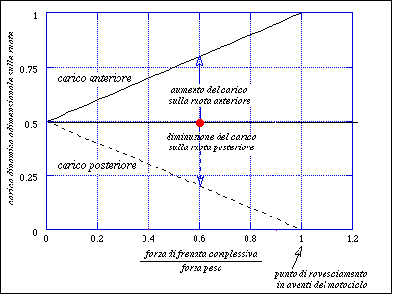
figura 3
Per un coefficiente di aderenza pari a 0.2 per entrambe le ruote si vede che il carico dinamico adimensionalizzato è circa 0.4 (40%) per la ruota posteriore e circa 0.6 (60%) per la ruota anteriore. Questo vuol dire che, per una frenata ottimale, la forza frenante totale sarà applicata per il 60% alla ruota anteriore e per il restante 40% alla ruota posteriore. Se il coefficiente di aderenza diventa 0.8 il carico dinamico sulla ruota anteriore passa a 0.9 (90%) mentre quello sulla ruota posteriore scende a 0.1 (10%). In questa nuova configurazione il contributo del freno posteriore diventa quasi trascurabile.
Si è visto che man mano che aumenta la forza massima frenante, aumenta il carico dinamico sulla ruota anteriore e diminuisce quello sulla ruota posteriore. Una condizione limite si raggiunge quando il carico dinamico sulla ruota posteriore si annulla, cioè quando la ruota posteriore comincia a sollevarsi. Questa condizione prende il nome di Frenata al limite del ribaltamento. La figura seguente mostra le forze in questa nuova configurazione:

figura 4
In questa situazione, il carico dinamico sulla ruota anteriore risulta uguale al peso del motociclo e la direzione della risultante del carico dinamico e della forza di frenata passa per il baricentro del motociclo.
L’equazione di equilibrio dei momenti rispetto al baricentro fornisce l’espressione della forza frenante al limite del ribaltamento:
![]()
![]() altro non è che il
minimo valore del coefficiente di aderenza fra pneumatico anteriore e sede
stradale necessario per arrivare al ribaltamento del
mezzo.
altro non è che il
minimo valore del coefficiente di aderenza fra pneumatico anteriore e sede
stradale necessario per arrivare al ribaltamento del
mezzo.
Con questo abbiamo concluso l’analisi delle forze che agiscono sulla motocicletta durante la frenata. Abbiamo visto che i carichi agenti sulle ruote non sono costanti ma variano al variare della forza frenante applicata nel punto di contatto tra pneumatico e superficie stradale; in particolare durante la frenata il carico sulla ruota anteriore aumenta, mentre quello sulla ruota posteriore diminuisce. L’aumento del carico sulla ruota anteriore consente a quest’ultima di trasmettere al suolo una forza maggiore prima di arrivare alla perdita di aderenza. La massima forza frenante viene trasmessa a terra proprio quando la ruota posteriore inizia a sollevarsi dal suolo. Questo spiega perché nelle competizioni molti piloti utilizzano solo i freni anteriori.