21/3/2000
Il modello matematico del pneumatico
Confronto tra simulazioni e realtÓ
Considerazioni sulla manovrabilitÓ
La prototipazione virtuale si occupa dello sviluppo di un prodotto interamente effettuato con l'ausilio del calcolatore elettronico, mediante l'utilizzo di appositi software e modelli matematici atti a simularne il comportamento reale.
In questo ambito sarÓ preponderante l'uso della "Multibody System Analysis", ossia dell'analisi cinematica e dinamica di corpi rigidi in movimento, opportunamente vincolati tra di loro.
Lo scopo di questo lavoro Ú la creazione di un modello virtuale di motociclo, nella fattispecie una Aprilia RSV 1000, e di un sistema di guida che siano capaci di simulare la percorrenza di tratti reali di strada.
Tra i vari codici multibody esistenti sul mercato, la scelta Ú ricaduta su MSC Working Model 3D per la sua potenza e flessibilitÓ d'uso.
Il modello risulta composto dai seguenti corpi rigidi: ruota anteriore e posteriore, forcellone posteriore, massa anteriore non sospesa, forcella anteriore, corpo moto e pilota.
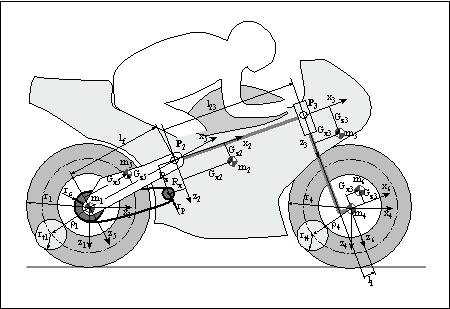
Le masse e le inerzie dei componenti, nonchŔ le caratteristiche delle sospensioni, sono quelle dichiarate dalla casa costruttrice; tutti i dati non noti sono stati misurati presso il laboratorio di Meccanica Applicata oppure stimati sulla base di altri motocicli di pari categoria.
Il calcolo delle forze e dei momenti agenti tra i pneumatici e la superficie stradale, ed il controllo che deve mantenere l'equilibrio e guidare il sistema moto-pilota lungo una predeterminata traiettoria, sono stati implementati in un software realizzato appositamente. Tale codice, chiamato "Easy Rider", Ú stato sviluppato in Visual Basic, e lavora accoppiato a Working Model attraverso la tecnologia OLE (Object Linking and Embedding).
In particolare ad ogni passo di integrazione Working Model passa a Easy Rider le posizioni e le velocitÓ lineari ed angolari delle ruote e del corpo moto, ricevendo a sua volta le forze e i momenti di contatto tra strada e pneumatico e la coppia da applicare allo sterzo per guidare la moto.
Il primo nucleo fondamentale di Easy Rider Ú sicuramente il modello matematico del pneumatico.
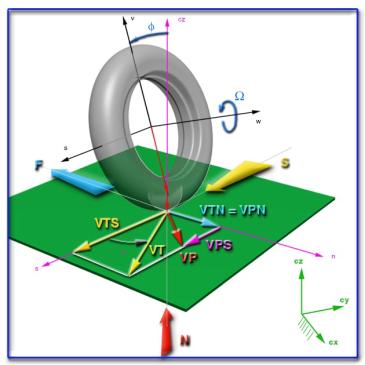
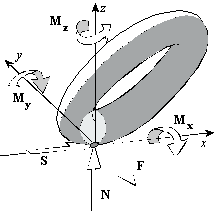
I dati di input, ricevuti da Working Model, sono le posizioni e le velocitÓ lineari ed angolari dei pneumatici; attraverso una serie di cambiamenti di coordinate viene calcolato il punto di contatto, la sua velocitÓ assoluta (VP) e quella di trascinamento (VT). A questo punto possiamo calcolare lo strisciamento longitudinale (slip) e l'angolo di deriva (indicato in figura con
La conoscenza di questi parametri Ú necessaria per il calcolo, effettuato con la "magic formula" di Pacejka, delle forze longitudinali, trasversali e verticali agenti sui pneumatici, nonch╚ dei momenti di torsione e di autoallineamento.
Il secondo nucleo fondamentale di Easy Rider Ú rappresentato dal controllo applicato sullo sterzo, che ha lo scopo di mantenere l'equilibrio del sistema moto-pilota e di guidarlo lungo una traiettoria predefinita.
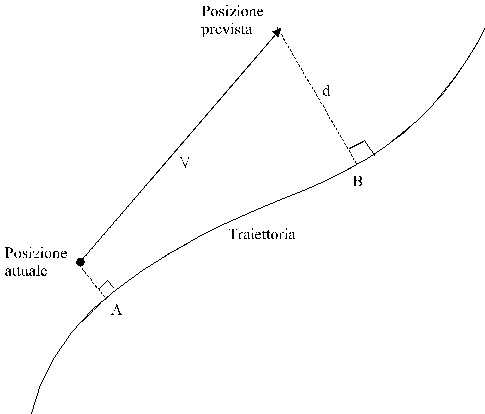
Tale controllo Ú basato sulla tecnica del "look ahead", che significa letteralmente "guardare avanti". Cosa fa infatti ogni pilota mentre guida? Guarda avanti, valuta la posizione che il mezzo potrebbe assumere rispetto alla traiettoria da seguire e quindi applica una coppia allo sterzo per correggere eventuali errori.
In maniera analoga si comporta il nostro controllo: considerando la configurazione attuale del motociclo (posizione e velocitÓ del centro di massa) esso calcola in che punto, dopo un determinato tempo "t", ci si troverebbe rispetto alla traiettoria stabilita. Sulla base di angolo di rollio, velocitÓ di rollio, distanza prevista dalla traiettoria e derivata temporale di tale distanza viene calcolata la coppia da applicare allo sterzo.
Il percorso da seguire Ú definito da una funzione parametrica X=X(L), Y=Y(L), dove X e Y sono le coordinate nel piano, L Ú il parametro lunghezza d'arco (spazio percorso). Allo scopo Ú stato creato un tool grafico per la generazione di traiettorie:
Il prototipo virtuale creato Ú stato sottoposto ad una serie di manovre standardizzate, come curve a raggio costante e slalom tra birilli equidistanti, effettuate a diverse velocitÓ; la stessa cosa Ú stata fatta con il motociclo reale, attrezzato con un sistema di telemetria. Sono state registrate e confrontate un'ampia serie di grandezze cinematiche e dinamiche; nei grafici seguenti si troveranno alcuni esempi di tali confronti.
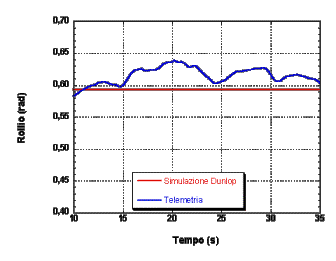
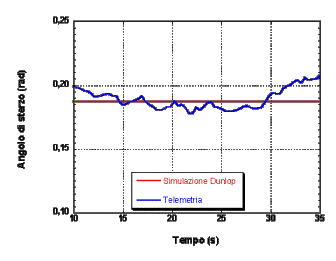
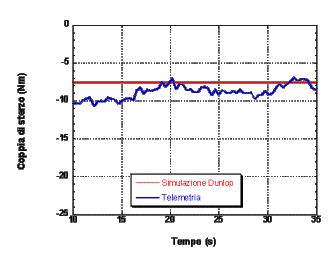
La corrispondenza tra dati di telemetria e simulazioni Ú molto buona, il che ci consente di affermare che il modello proposto Ú accurato.
Si noti in particolare il valore della coppia di sterzo: esso Ú negativo, e questo significa che se stiamo percorrendo ad esempio una curva in senso orario, la coppia da esercitare per mantenere la moto in equilibrio ha verso opposto (ossia antiorario); in gergo motociclistico questo si dice "tener su la moto".
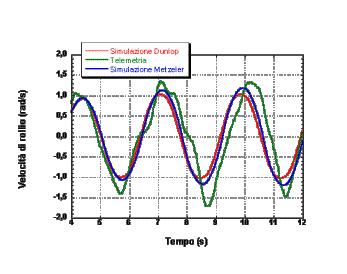
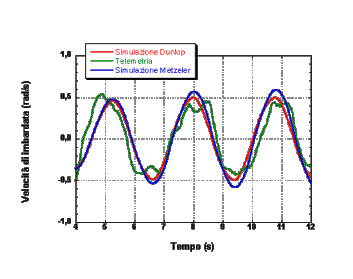
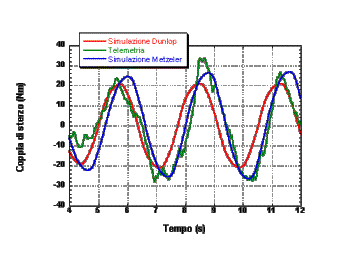
Le simulazioni sono state effettuate utilizzando i dati di due pneumatici differenti: Dunlop (pneumatico da competizione) e Metzeler (pneumatico normale); le differenze sono piccole, visto che le manovre in cui Ú stata impegnata la moto non erano al limite.
Dopo aver verificato l'accuratezza del modello virtuale, esso Ú stato sottoposto ad una serie di manovre a rollio costante e a raggio di curvatura costante, con velocitÓ che spaziano da 5 m/s fino ai limiti di aderenza dei pneumatici.
Vediamo ad esempio come varia l'angolo di sterzo nelle curve a raggio costante, in funzione dell'accelerazione laterale:
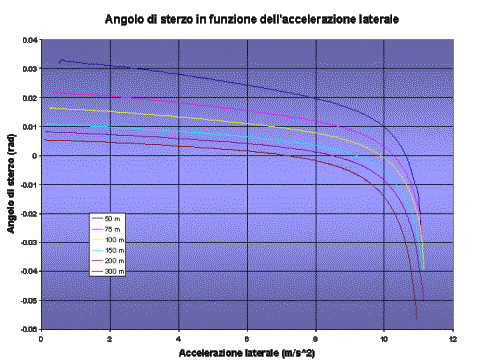
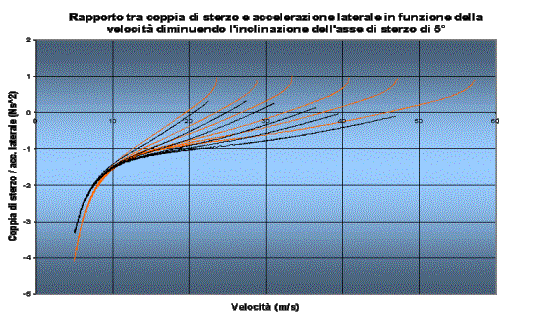
Un parametro molto interessante per definire la manovrabilitÓ di un motociclo Ú il rapporto tra coppia di sterzo ed accelerazione laterale in funzione della velocitÓ.
Come si pu┌ notare dal grafico seguente si ottiene una famiglia di curve "a pettine", che caratterizza la configurazione geometrica ed inerziale attuale del motociclo.
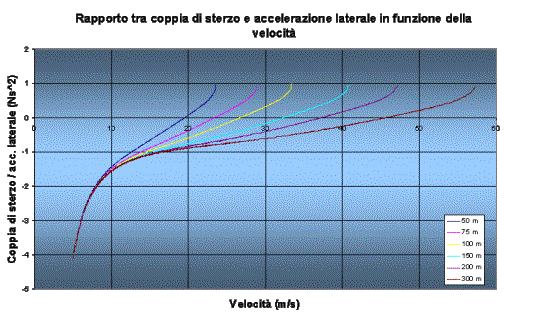
Vediamo cosa succede se, ad esempio, diminuiamo l'inclinazione dell'asse di sterzo di 5░. Si ottiene una nuova famiglia di curve (in nero), spostata verso il basso e verso sinistra. Considerando che una manovrabilitÓ ottima implica delle curve abbastanza vicine allo zero, possiamo dire che la modifica fatta peggiora la situazione; in pi¨ si nota che le nuove curve sono pi¨ corte e spostate a sinistra, e questo significa un decadimento delle prestazioni al limite di aderenza.
Alla luce del lavoro svolto si pu┌ affermare che Ú stata raggiunta una buona aderenza delle simulazioni con la realtÓ, in una vasta casistica di manovre tipiche. In pi¨ Ú stato sviluppato un controllo innovativo che consente di simulare la percorrenza di tratti reali di strada. Sono state tratte delle interessanti indicazioni sulla manovrabilitÓ dei motocicli, ed Ú stato sviluppato un software (Easy Rider) potente, flessibile e facile da usare.
Terna assoluta di riferimento: essa Ú solidale alla strada, ed il suo asse Z Ú ad essa perpendicolare.
Terna solidale al motociclo: l'asse Z di questa terna Ú verticale rispetto alla moto, l'asse X Ú longitudinale, l'asse Y Ú trasversale.
Rollio: angolo di inclinazione tra l'asse verticale Z perpendicolare alla strada ed il piano di simmetria contenente il motociclo (definito dagli assi Z e X della terna solidale alla moto). In gergo motociclistico definisce di quanto la moto si "piega" rispetto alla verticale.
Imbardata: rotazione attorno all'asse Z perpendicolare alla strada, appartenente alla terna fissa, della moto.
Beccheggio: rotazione attorno all'asse Y della terna solidale alla moto. Un esempio di beccheggio si ha in accelerazione o in frenata, quando la moto rispettivamente si inclina all'indietro o in avanti.
Coppia di sterzo: per effettuare una curva con una moto il pilota, con le sue braccia, ruota il manubrio. L'azione di tutte queste forze Ú semplicemente riducibile ad una coppia agente sull'asse di sterzo.