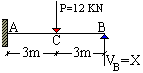
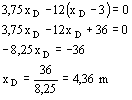Metodo degli abbassamenti. Problema. Tracciare i diagrami delle sollecitazioni della trave in figura. Si utilizzi il metodo degli abbassamenti per la determinazione dell'incognita iperstatica. |
|
|
La trave ha tre gradi di libertà e quattro limitazioni vincolari, tre delle quali offerte dall'incastro ed una dal carrello: si tratta perciò di una struttura caratterizzata da un grado di perstaticità. |
|
Assunta quale incognita iperstatica la reazione VB occorre determinare il valore di X che consente al punto B di non abbassarsi, in modo da conservare la congruenza con il comportamento del carrello di partenza. |
L'abbassamento, positivo, hBP provocato dal carico P deve essere compensato dall'innalzamento, negativo, hBX prodotto dalla reazione iperstatica X, in modo che il punto B, vincolato con il carrello, non si sposti. |
La deformazione nell'estremo B hB, applicando il principio di sovrapposizione degli
effetti, è fornita dalla sommatoria dell'abbassamento hBP
provocato dal carico P agente sulla trave e dal sollevamento hBX
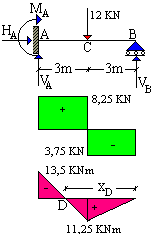
prodotto dalla reazione iperstatica X. Poiché deve essere hB = 0, si ha hBP + hBX = 0 nella quale, rispettando la convenzione di segno, il termine hBX è negativo. Noti il valore di hBP ed il valore di hBX si ha
|
 |
Possono ora essere calcolate le altre reazioni
vincolari: HA = 0 VA = 12 - 3,75 = 8,25 KN MA = 3,75 ´ 6 - 12 ´ 3 = -13,5 KNm Il diagramma del taglio è costante nei due tratti AC e CB:
Il diagramma dei momenti ha andamento lineare con un massimo nel punto C, punto a taglio nullo:
Il momento si annulla nel puntoD MD = 0
|