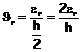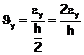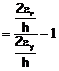NTC08. Classificazione
delle sezioni.
La capacità rotazionale delle
sezioni.
Le Norme Tecniche
prevedono tre diverse modalità di calcolo strutturale:
|
Metodo |
Modalità di calcolo |
|
Metodo elastico (E) |
Si assume un
comportamento elastico lineare del materiale, sino al raggiungimento della
condizione di snervamento. Il metodo può
applicarsi a tutte le classi di sezioni, con l’avvertenza di riferirsi al
metodo delle sezioni efficaci o a metodi equivalenti, nel caso di sezioni di
classe 4. |
|
Metodo plastico (P) |
Si assume la
completa plasticizzazione del materiale. Il metodo può
applicarsi solo a sezioni di tipo compatto, cioè di classe 1 e 2. |
|
Metodo elasto-plastico (EP) |
Si assumono
legami costitutivi tensione-deformazione del materiale di tipo bilineare o
più complessi. Il metodo può
applicarsi a qualsiasi tipo di sezione. |
La
scelta tra le tre modalità è incentrata su una suddivisione in quattro classi delle
sezioni, effettuata in base alla loro capacità rotazionale Cq definita
come:
essendo
qr e qy le curvature corrispondenti
rispettivamente al raggiungimento della deformazione ultima ed allo
snervamento.
|
|
La formula precedente può essere
riscritta come
In
altri termini la capacità rotazionale è data dal rapporto tra la quota di
rotazione plastica e quella elastica. |
Classificazione delle sezioni.
Le classi previste
dalle Norme Tecniche risultano le seguenti:
|
Classe |
Tipo sezione |
Caratteristica |
|
1 (sezione compatta) |
|
la sezione è in
grado di sviluppare una cerniera plastica avente la capacità rotazionale
richiesta per l’analisi strutturale condotta con il metodo plastico senza
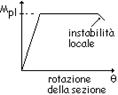
subire riduzioni della resistenza. Possono generalmente classificarsi come
tali le sezioni con capacità rotazionale |
|
2 (sezione compatta) |
|
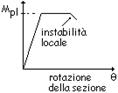
la sezione è in
grado di sviluppare il proprio momento resistente plastico, ma con capacità
rotazionale limitata. Possono generalmente classificarsi come tali le sezioni
con capacità rotazionale |
|
3 (sezione
moderatamente snella) |
|
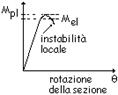
le tensioni
nella sezione calcolate nelle fibre estreme compresse possono raggiungere la
tensione di snervamento, ma l’instabilità locale impedisce lo sviluppo del
momento resistente plastico |
|
4 (sezione snella) |
|
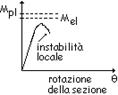
per determinarne
la resistenza flettente, tagliante o normale, è necessario tener conto degli
effetti dell’instabilità locale in fase elastica nelle parti compresse che
compongono la sezione. In tal caso nel calcolo della resistenza la sezione
geometrica effettiva può sostituirsi con una sezione efficace |
|
|
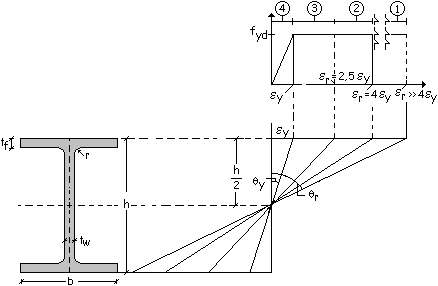
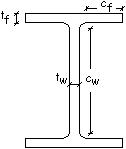
Facendo
riferimento ad un profilo IPE e considerando la sostanziale equivalenza che
si verifica tra angoli molto piccoli
espressi in radianti e la loro tangente, si ha
Posto
si ricava
Analogamente si
ha
|
In
pratica, per sezioni molto compatte ( ad es. una sezione rettangolare non
sottile) che non presentano problemi di instabilità il materiale può utilizzare
al massimo la sua duttilità ed è
Per
i profilati di impiego comune la deformazione di rottura è limitata dai
fenomeni di imbozzamento originati dall’instabilità delle diverse parti che
compongono la sezione (anima, flange, ecc..) in zona compressa. E’ il caso
delle sezioni compatte (
) e moderatamente snelle (
).
Infine,
nel caso di
la
tensione non raggiunge il limite di snervamento fyd; in questa
evenienza, nel calcolo si fa riferimento ad una sezione efficace caratterizzata
da componenti di lunghezza teorica ridotta rispetto a quella effettiva, in
misura utile a prevenirne l’imbozzamento (sezione snella).
Poiché, come si è detto, è il fenomeno
dell’instabilità a produrre una riduzione della capacità rotazionale, le Norme
Tecniche in sintonia con l’Eurocodice 3 classificano le sezioni a partire dalla
snellezza delle sue componenti.
|
|
I limiti di Cq
stabiliti dalle Norme Tecniche non sono presenti nell’EC3. Ai fini pratici
tali limiti hanno una scarsa utilità poiché i parametri per la
classificazione delle sezioni non fanno riferimento ad essi in maniera
diretta. |
Il fenomeno dell’imbozzamento.
Le diverse sezioni
commerciali possono essere viste come il risultato dell’unione di elementi di
area modesta in rapporto alla loro lunghezza.
|
|
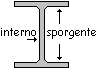
Gli
elementi possono essere considerati interni,
se confinati su più lati come ad esempio l’anima di un profilo IPE, o sporgenti, se confinati da un solo
lato come l’ala di un profilo IPE. Essi possono essere soggetti al fenomeno
dell’imbozzamento, dovuto all’instabilità locale, quando compressi per sforzo
normale o a causa della flessione. |
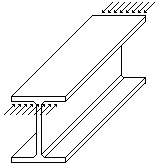
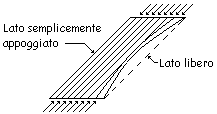
Si
consideri, ad esempio, l’ala superiore di un profilo IPE assoggettato a
flessione con un momento positivo; essa risulta compressa longitudinalmente e,
per effetto dell’instabilità locale, può imbozzarsi lungo il lato libero. L’ala
inferiore, assoggettata a trazione, non è interessata al problema.
Il
fenomeno si verifica se la snellezza dell’elemento è elevata: in questo caso il
suo cedimento avviene per carico di punta euleriano; per snellezze limitate, la
rottura avviene, invece, per compressione semplice.
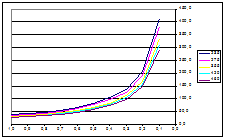
Riportando
su un grafico normalizzato la variazione del carico sopportabile in funzione
della snellezza si ottiene l’andamento evidenziato nella figura seguente
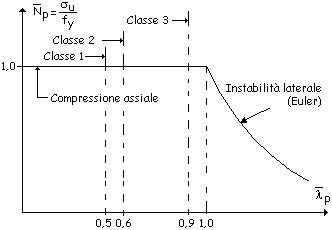
La
grandezza adimensionale 
esprime il rapporto tra il carico ultimo e quello
corrispondente allo snervamento; la grandezza adimensionale 
dipende dal rapporto tra la tensione di snervamento e quella
critica euleriana.
I
valori limite di lp corrispondenti alle prime tre classi sono evidenziati in
figura; la quarta classe corrisponde al ramo iperbolico euleriano del
diagramma.
Il
diagramma viene tracciato per la sola tensione di snervamento 
. I suoi valori possono essere utilizzati anche per altre
tensioni mediante il coefficiente e i cui valori sono riportati di seguito.
|
fy |
235 |
275 |
355 |
420 |
460 |
|
|
1 |
0,92 |
0,81 |
0,75 |
0,71 |
|
|
L’EC3
utilizza il simbolo e anche per le deformazioni unitarie. Non
v’è, ovviamente, nessuna relazione tra le due grandezze. |
La determinazione della classe.
|
|
Seguendo
le regole stabilite dalle Norme Tecniche (e dall’EC3) l’assegnazione della
classe di appartenenza della sezione si presenta relativamente semplice:
|
mentre per l’ala è 
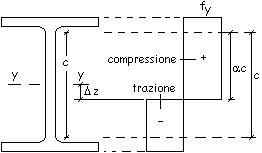
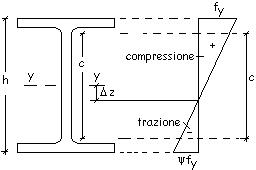
Ad
esempio per l’anima di un profilo IPE si ottiene il quadro sinottico seguente
|
Classe |
Flessione |
Compressione |
Flessione e Compressione |
|
1 |
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
|
E’
utilizzato il segno + per le tensioni di compressione ed il segno – per
quelle di trazione. |
Per
l’ala dello stesso profilo si ha, a compressione,
|
Classe 1 |
Classe 2 |
Classe 3 |
|
|
|
|
Sostituendo
i valori numerici, per l’anima si ha, a flessione:
|
|
fy |
235 |
275 |
355 |
420 |
460 |
|
|
e |
1,0 |
0,92 |
0,81 |
0,75 |
0,71 |
|
|
1 |
72 |
66,24 |
58,32 |
54 |
51,12 |
|
Classe |
2 |
83 |
76,36 |
67,23 |
62,25 |
58,93 |
|
|
3 |
124 |
114,08 |
100,44 |
93 |
88,04 |
Per
l’anima, a compressione:
|
|
fy |
235 |
275 |
355 |
420 |
460 |
|
|
e |
1,0 |
0,92 |
0,81 |
0,75 |
0,71 |
|
|
1 |
33 |
30,36 |
26,73 |
24,75 |
23,43 |
|
Classe |
2 |
38 |
34,96 |
30,78 |
28,5 |
26,98 |
|
|
3 |
42 |
38,64 |
34,02 |
31,5 |
29,82 |
Per
l’anima, a pressoflessione, Classe 1, è
|
fy |
235 |
275 |
355 |
420 |
460 |
|
a |
1,0 |
0,92 |
0,81 |
0,75 |
0,71 |
|
1,0 |
33,0 |
30,4 |
26,7 |
24,8 |
23,4 |
|
0,9 |
37,0 |
34,0 |
30,0 |
27,8 |
26,3 |
|
0,8 |
42,1 |
38,8 |
34,1 |
31,6 |
29,9 |
|
0,7 |
48,9 |
45,0 |
39,6 |
36,7 |
34,7 |
|
0,6 |
58,2 |
53,6 |
47,2 |
43,7 |
41,3 |
|
0,5 |
72,0 |
66,2 |
58,3 |
54,0 |
51,1 |
|
0,4 |
90,0 |
82,8 |
72,9 |
67,5 |
63,9 |
|
0,3 |
120,0 |
110,4 |
97,2 |
90,0 |
85,2 |
|
0,2 |
180,0 |
165,6 |
145,8 |
135,0 |
127,8 |
|
0,1 |
360,0 |
331,2 |
291,6 |
270,0 |
255,6 |
|
0,001 |
36000,0 |
33120,0 |
29160,0 |
27000,0 |
25560,0 |
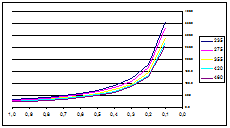
Per
l’anima, a pressoflessione, Classe 2, è
|
fy |
235 |
275 |
355 |
420 |
460 |
|
a |
1,0 |
0,92 |
0,81 |
0,75 |
0,71 |
|
1,0 |
38,0 |
35,0 |
30,8 |
28,5 |
27,0 |
|
0,9 |
42,6 |
39,2 |
34,5 |
32,0 |
30,3 |
|
0,8 |
48,5 |
44,6 |
39,3 |
36,4 |
34,4 |
|
0,7 |
56,3 |
51,8 |
45,6 |
42,2 |
40,0 |
|
0,6 |
67,1 |
61,7 |
54,3 |
50,3 |
47,6 |
|
0,5 |
83,0 |
76,4 |
67,2 |
62,3 |
58,9 |
|
0,4 |
103,8 |
95,5 |
84,0 |
77,8 |
73,7 |
|
0,3 |
138,3 |
127,3 |
112,1 |
103,8 |
98,2 |
|
0,2 |
207,5 |
190,9 |
168,1 |
155,6 |
147,3 |
|
0,1 |
415,0 |
381,8 |
336,2 |
311,3 |
294,7 |
|
0,001 |
41500,0 |
38180,0 |
33615,0 |
31125,0 |
29465,0 |
Per
l’anima, a pressoflessione, Classe 3, è
|
fy |
235 |
275 |
355 |
420 |
460 |
|
y |
1,0 |
0,92 |
0,81 |
0,75 |
0,71 |
|
-2,0 |
263,0 |
242,0 |
213,1 |
197,3 |
186,8 |
|
-1,8 |
232,9 |
214,3 |
188,7 |
174,7 |
165,4 |
|
-1,6 |
203,9 |
187,6 |
165,2 |
152,9 |
144,8 |
|
-1,4 |
176,1 |
162,0 |
142,6 |
132,0 |
125,0 |
|
-1,2 |
149,4 |
137,5 |
121,0 |
112,1 |
106,1 |
|
-1,0 |
124,0 |
114,1 |
100,4 |
93,0 |
88,0 |
|
-0,8 |
103,4 |
95,2 |
83,8 |
77,6 |
73,4 |
|
-0,6 |
89,0 |
81,9 |
72,1 |
66,7 |
63,2 |
|
-0,4 |
78,1 |
71,8 |
63,2 |
58,6 |
55,4 |
|
-0,2 |
69,5 |
64,0 |
56,3 |
52,2 |
49,4 |
|
0,0 |
62,7 |
57,7 |
50,8 |
47,0 |
44,5 |
Per
l’ala si ottiene, a compressione:
|
|
fy |
235 |
275 |
355 |
420 |
460 |
|
|
e |
1,0 |
0,92 |
0,81 |
0,75 |
0,71 |
|
|
1 |
9 |
8,28 |
7,29 |
6,75 |
6,39 |
|
Classe |
2 |
10 |
9,2 |
8,1 |
7,5 |
7,1 |
|
|
3 |
14 |
12,88 |
11,34 |
10,5 |
9,94 |
I sagomari.
La classe della
sezione è riportata nei sagomari diffusi dalle ditte produttrici dei profili
commerciali.
Usualmente sono
presenti le classi attribuite alla sezione per i diversi tipi di acciaio,
distinte per compressione e flessione.
