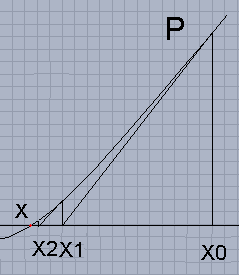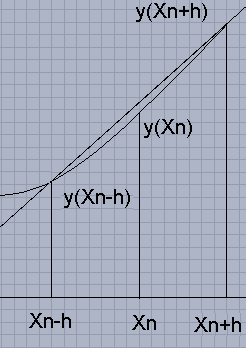C'è un legame molto stretto tra un'equazione di secondo grado ax2+bx+c=0 ed un particolare luogo geometrico: la parabola, essa è definita come l'insieme dei punti P del piano equidistanti da un punto F detto fuoco e da una retta chiamata direttrice
dalla definizione si ottiene, dopo alcune elaborazioni, l'equazione
y=ax2+bx+c
dove il secondo membro dell'equazione, eguagliato a zero, rappresenta proprio un'equazione di secondo grado, quindi le soluzioni dell'equazione ax2+bx+c=0 possono essere intese come una parte delle soluzione del sistema
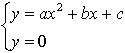
cioè le ascisse dei punti di intersezione del grafico della parabola con l'asse delle ascisse.
Questo modo di intendere suggerisce un metodo grafico per la ricerca delle soluzioni di un'equazione di secondo grado, tra i tanti ne viene qui riportato uno dei più noti: il metodo di Newton
| A
partire da xo
si conduce la perpendicolare fino ad incontrare la parabola nel punto P(x0,y(x0)),
poi di traccia la tangente la cui equazione è
che interseca l'asse delle ascisse in x1, poi la costruzione viene reiterata utilizzando la formula ricorsiva, ottenuta dalla relazione precedente isolando x ed introducendo gli indici
si ottiene una successione di punti che converge alla soluzione x |
|
|
Una variante del metodo di Newton è il metodo della secante. In questo caso invece di utilizzare il concetto di tangente che richiede la conoscenza del concetto di derivata, si approssima la retta tangente con la retta secante. La formula ricorsiva
la differenza tra la retta tangente e la secante è tanto più piccola quanto più si sceglie piccolo h. Il metodo della secante è utilizzato anche per trovare in generale le soluzioni reali di una equazione. Il programma in TurboPascal risolve l'equazione xex -1=0 ed opportunamente modificato può essere utilizzato per risolvere altre equazioni, è sufficiente andare nel programma e ridefinire la linea f:=x*exp(x)-1; |
|