Sia F(p,q) il fuoco
della parabola, P(x,y) un suo generico punto e
y=d l’equazione della direttrice,
imponiamo che
![]()
elevando al quadrato e isolando y
si ottiene
![]()
![]()
![]()
si
ottiene: y=ax2+bx+c
risolvendo il sistema
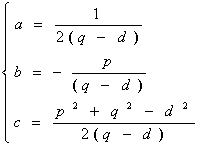
rispetto alle variabili
p,q,d si ottiene dopo qualche passaggio:
![]()
e quindi le coordinate del fuoco e l’equazione della direttrice sono:
![]()
mentre l’equazione dell’ asse
di simmetria della parabola ed il vertice
V (punto di intersezione tra il grafico della parabola e l’asse di simmetria,
ed anche punto medio del segmento che congiunge il fuoco col punto di
intersezione tra asse e direttrice della parabola) assumono la forma:
![]()