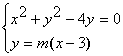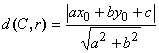Primo metodo (algebrico)
La tangente ad una circonferenza, abbiamo già visto a proposito della mutua posizione tra circonferenza e retta, si ha quando D = 0. La ricerca della tangente ( retta passante per un punto Po(xo,yo)) del tipo y=m(x-xo)+yo ad una circonferenza si può affrontare imponendo che il sistema
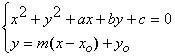 |
 |
Si nota che al variare di m
variano le intersezioni tra circonferenza e retta.
P |
abbia due soluzioni coincidenti. Sostituendo y nella prima equazione di ottiene una equazione di secondo grado nell'incognita x e nel parametro m che rappresenta in realtà la variabile da determinare per trovare la retta tangente, tale parametro di ottiene risolvendo l'equazione D = 0.
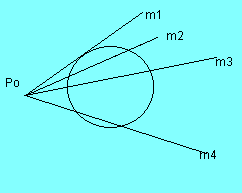
| Po appartiene alla circonferenza | Po è esterno | Po interno | |
| possiamo distinguere 3 casi | 
una retta tangente |
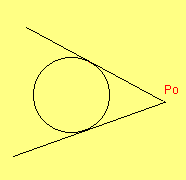
due rette tangenti |

nessuna retta tangente |
|
esempio |
Data la circonferenza C : x2+y2-4y=0, determinare le rette tangenti a C passanti per P(3,0) | |
| Imponiamo
che il sistema
abbia due soluzioni coincidenti. Per sostituzione di ottiene |
||
|
|
||
| che
avrà soluzioni coincidenti se D/4=
0
cioè
|
||
| e le rette tangenti: y=0 e y=-12/5(x-3) | ||
La seguente successione di figure propone la costruzione geometrica della retta passante per un punto P e tangente ad una circonferenza.
|
Passo per passo viene qui proposta la costruzione della retta tangente condotta da un punto P ad una circonferenza. Le figure sono state generate con Il software Cindirella e sono attive, puoi muovere i punti rossi ed aumentare il raggio della circonferenza. Alla base della costruzione c'è una proprietà della circonferenza: Un triangolo inscritto in una semicirconferenza è rettangolo.
|
|||
Secondo metodo (geometrico)
Il metodo appena descritto risulta essere abbastanza pesante dal punto di vista dei calcoli, per trovare la retta tangente si può operare in un altro modo, sfruttando una proprietà della circonferenza:
proprietà: la distanza dal centro di una circonferenza ad una retta tangente ad è pari al raggio.
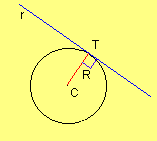 |
r: ax+by+c=0 Po(xo, yo) |
La distanza del punto C dalla retta tangente passante per Po è data dalla nota formula per cui imponendo che d(C,r) = R, si ottiene una equazione nell'incognita m, che una volta risolta fornisce il valore/i di m che risolvono il problema.
|
esempio |
Data la circonferenza C : x2+y2-4y=0, determinare le rette tangenti a C passanti per P(3,0) |
| Il
centro della circonferenza è C(0,2) ed il
raggio R=2. il fascio di rette passante per P(3,0)
è r: y=m(x-3) che in forma implicita assume la forma mx-y-3m=0.
Imponendo che d(P,r)=2 si ottiene l'equazione
in m
che risolta da come soluzioni m1=0 ed m2= -12/5. Osserviamo che l'esercizio risolto in questo modo richiede meno elaborazioni rispetto al metodo algebrico. |
Terzo metodo (formula di sdoppiamento)
Questo metodo si applica solo nel caso in cui il punto Po dal quale deve passare la retta tangente è un punto appartenente alla circonferenza di equazione:
![]()
e sarà quindi anche verificata la condizione
per cui sottraendo membro a membro si ottiene:
![]() (1)
(1)
mentre la retta generica per Po ha equazione
![]() (2)
(2)
scomponendo in fattori le differenze dei quadrati della (1) e sostituendo la (2) nella (1) si ottiene (imponendo che Po verifichi l'equazione della retta)
![]()
ed infine la formula di sdoppiamento
![]()